时间性去噪

思路及方法

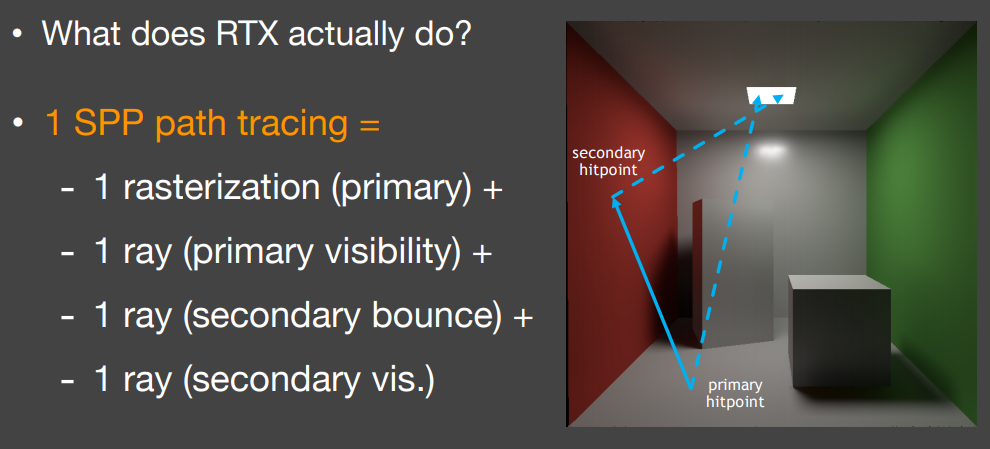
RTX目前可能仅支持1SPP，每像素一采样，即像素到场景一条光线（可用光栅化替代），该交点再生成一条采样光线

仅有1SPP意味着噪声成为了实时光追的关键问题

由于实时渲染效率要求极高，一系列滤波方法都不能胜任，包括Sheared filtering（切变滤波）、离线渲染中的滤波方法、深度学习方法

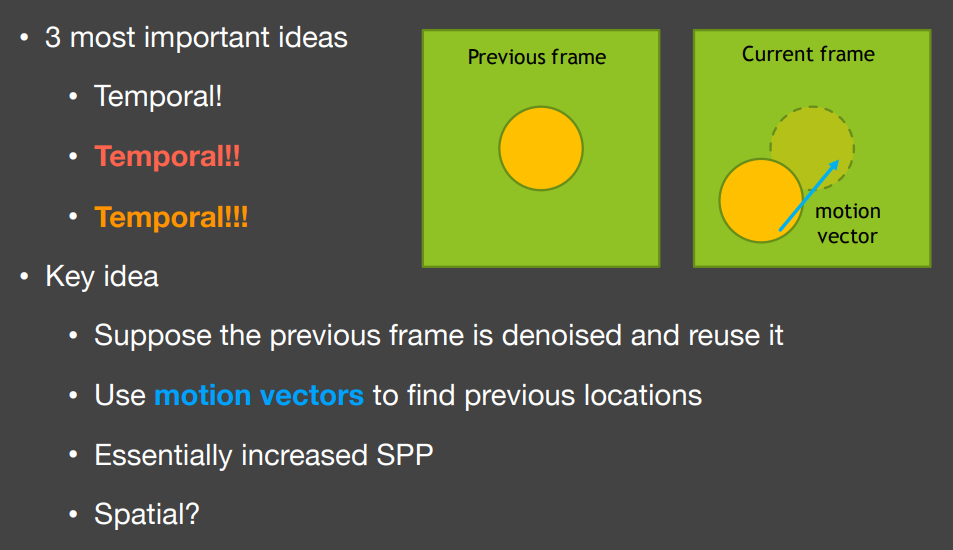
因此工业界采用motion vector的方法，即利用上一帧的信息进行时间上的复用（假设上一帧已去噪），相当于增加采样数（SPP）

利用Back Projection的方法求当前帧中某一像素在上一帧中的位置

具体步骤如上图，思路是先求当前帧该像素的世界坐标方法是在Gbuffer中直接保存或者矩阵变换计算（仍然需要深度值z，矩阵变换针对xy），然后易得世界坐标下该点的运动，求出上一帧中该点的世界坐标，最后矩阵变换求出上一帧中该点的屏幕坐标

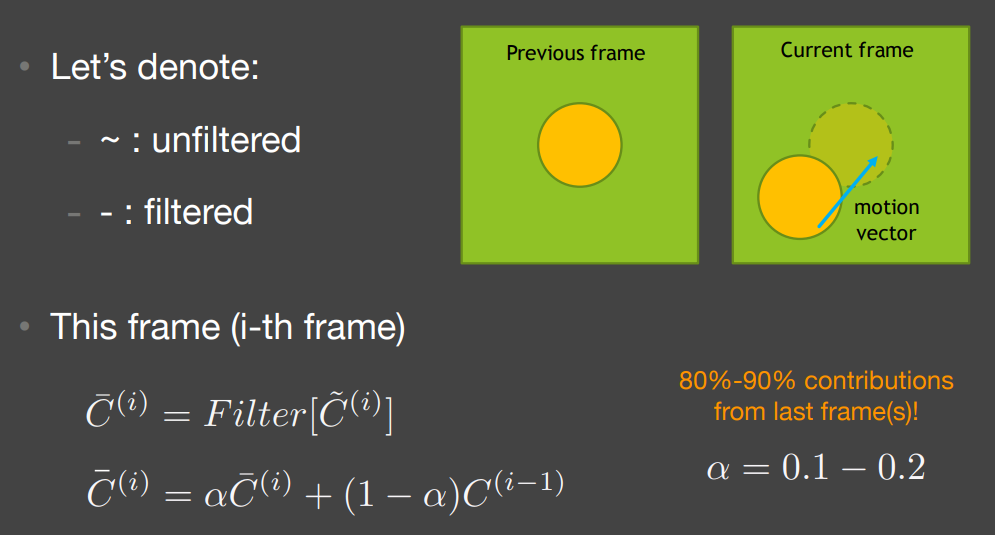
取得上一帧对应点的像素颜色，与当前帧进行混合，当前帧的比例可能仅占一到二成

问题

由几何信息变化引起

场景、镜头快速切换

屏幕空间信息局限

遮挡关系的变化，造成拖影

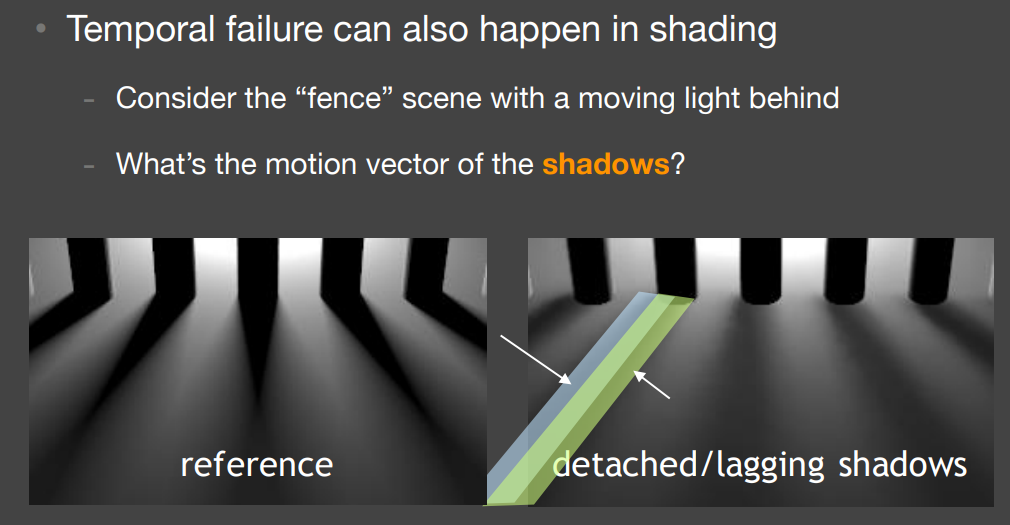
由着色信息变化引起

地面上阴影的变化

反射景象中的变化

针对问题的调整

clamping方法：将上一帧的颜色截取到当前帧颜色附近的范围

detection方法：物体编号，若上一帧与当前帧的对应像素属于不同物体，则可能丢弃上一帧结果

由于不同程度的舍弃上一帧信息而导致引入更多噪声

空间性去噪

高斯滤波

高斯滤波的算法实现，针对每像素周围的一部分像素（包括自身），以高斯函数的值为权重进行滤波（函数参数为周围像素到中心像素的距离），累加带权重颜色值，同时累加权重，最后除以总权重值进行归一化

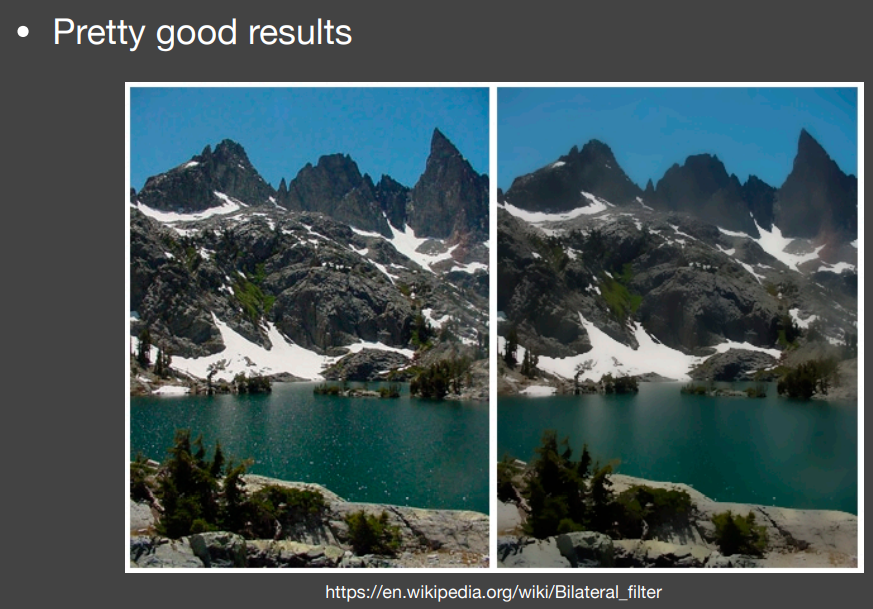
双边滤波（Bilateral filtering）

普通的高斯滤波使边缘模糊

双边滤波目的是保留清晰的边缘

边缘意味着颜色的剧烈变化

因此在滤波过程中，当考虑周围像素对中央像素的贡献时，若周围像素的颜色与中央像素的颜色相差巨大，则减少其贡献

上图公式中ij，kl分别为两像素坐标，右侧指数部分前半部分为距离因素的考量（同高斯滤波），后半为颜色因素的考量（颜色差距大则减少权重）

结果如下

保留了清晰的边缘但仍会丢失细节信息

联合双边滤波（Joint Bilateral Filtering）

高斯滤波考虑距离因素进行权重的衰减

双边滤波考虑距离和颜色因素进行权重的衰减

由此启发得到联合双边滤波，其考虑更多样的因素进行权重的衰减

由于渲染过程中利用Gbuffer可以方便的获取多种屏幕空间信息，例如世界坐标、法线、漫反射颜色（albedo）等，这些都是通过光栅化得到的无噪声图像信息

具体例子如图中康奈尔盒子所示

A点对B点的权重贡献因为深度相差大而进行较多的衰减（保留物体与背景物体之间的边缘）

B点对C点的权重贡献因为法线相差大而进行较多的衰减（保留同物体不同面的折痕边缘）

D点对E点的权重贡献因为颜色值相差大而进行较多的衰减（保留阴影边缘）

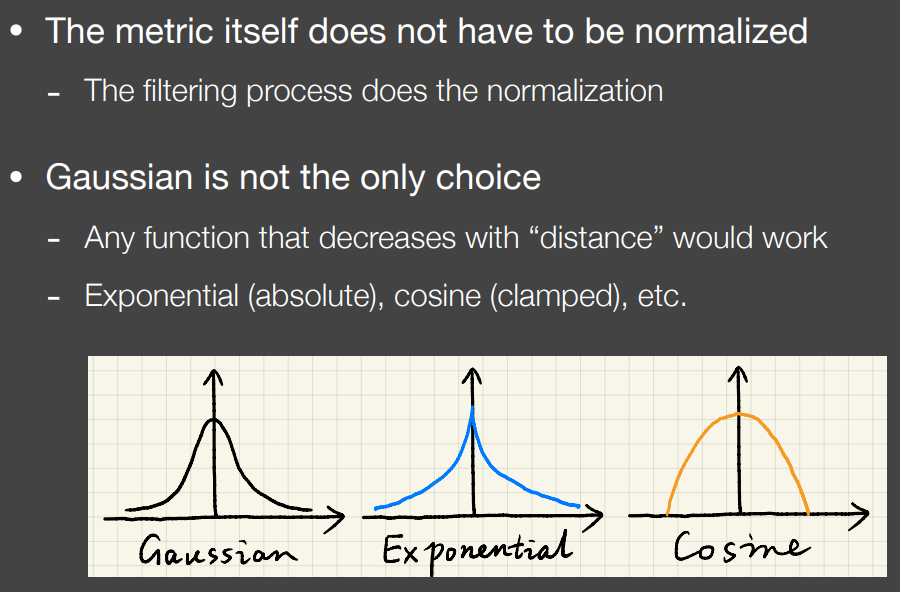
不一定利用高斯函数，任何随距离衰减的函数都是可能的选择

大尺寸滤波核的实现

进行滤波操作时，若核的大小达到64$\times$64则直接的遍历开销难以承担

分趟实现（Separate Passes）

第一个pass先只在竖直方向进行滤波，第二个pass对结果进行水平方向的滤波（单一方向的滤波也只使用一维的函数），将总共$N\times N$次操作减少到$N+N$

该方法的原理如上图所示

考虑高斯滤波，二维高斯函数半身可以拆分为两个一维高斯函数，在滤波对应的卷积操作中（图中$F(x_0,y_0)$疑为$F(x,y)$），可在进行二次积分时将高斯函数拆分开，再分别进行一维的卷积，即对应于竖直和水平方向的两次单独的一维滤波

然而高斯滤波以外的方法理论上不能保证函数可拆分，故在使用其他滤波方法的情况不完全准确

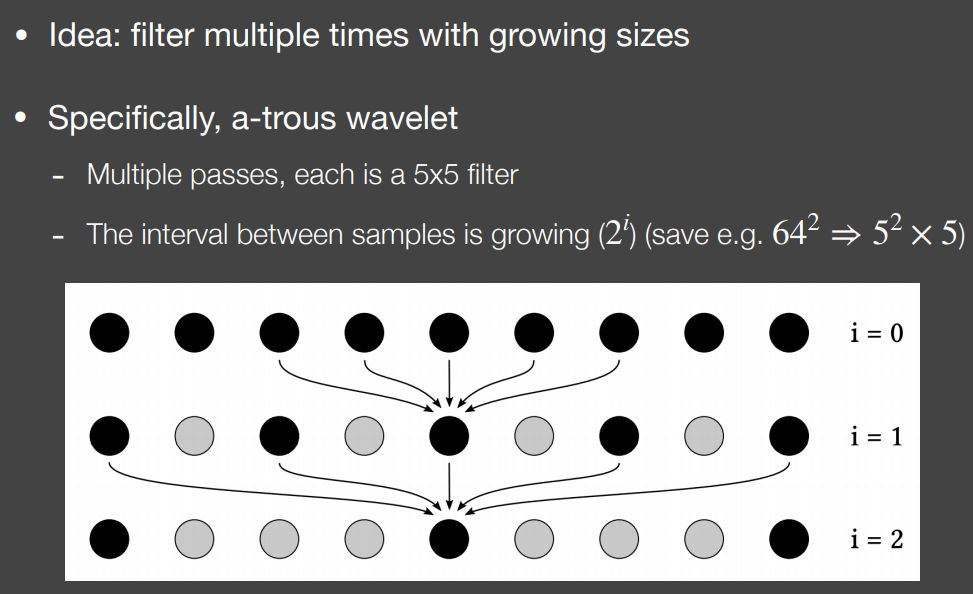
尺寸递增（Progressively Growing Sizes）

同样分pass实现，每个pass只进行$5\times 5$的滤波

下一次pass将以更大的距离跳跃选择采样点进行$5\times 5$的滤波，跳跃距离为$2^i$，$i$为当前已进行的pass数（如图中所示从0递增）

利用跳跃采样的方法实际上也扩大了滤波覆盖的面积

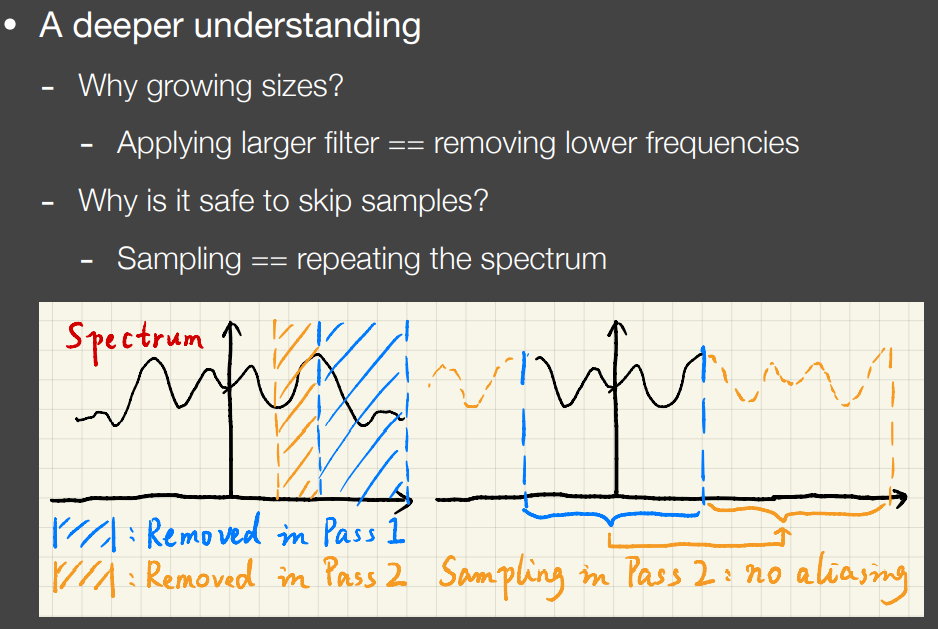
该方法原理的理解需要信号相关的进一步的知识

大致意思为，在频谱图上扩大滤波尺寸相当于消除更低频率的信息，而采样操作相当于频谱移动。理想状况下前一个pass中消除了高频信息留下空白部分，当前pass进行跳跃采样使保留的低频信息转移到原来高频信息所在的空白部分，未发生频谱重叠则没有走样现象（aliasing）

Outlier Removal（亮点去除）

图中有时会出现特别亮的噪点，若直接进行滤波，其亮度值会分摊到周围像素，使滤波效果更差，需要考虑在滤波前处理这些特别亮的噪点

判定亮点的方法是对每个像素，计算其周围较小范围内的均值和方差，利用均值和方差确定亮度的合理范围（比如$\mu\pm{k\sigma}$），超出此范围判定成亮点，并进行clamp操作

Spatiotemporal Variance-Guided Filtering (SVGF)

综合了时间空间的去噪策略，加入方差因素和一些其他技巧

以下为SVGF与联合双边滤波相比，具有的特点

其中对Luminance（颜色灰度值）的考量体现了SVGF中的Variance（用来减少阴影中较亮的噪点在滤波中的权重）