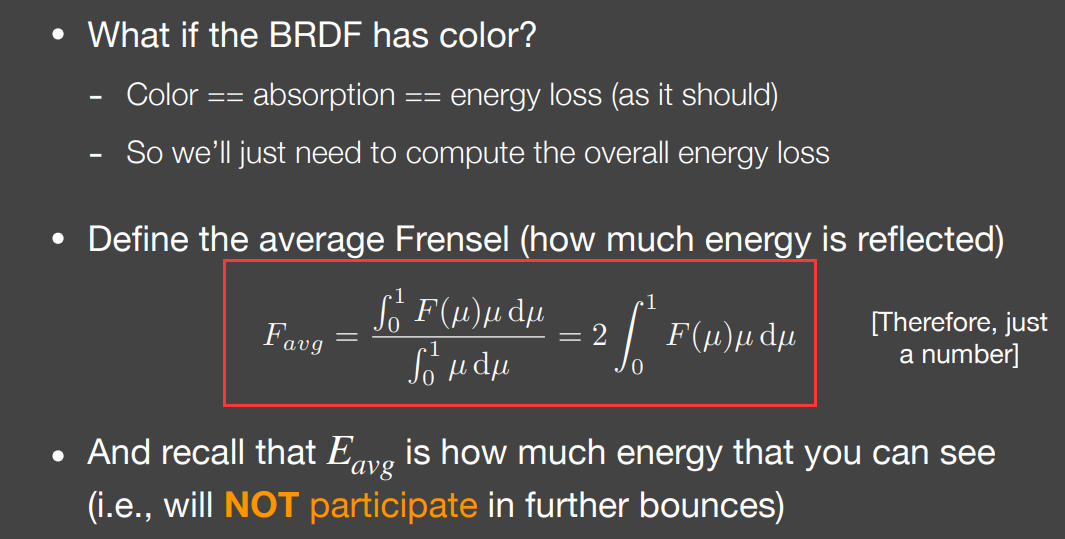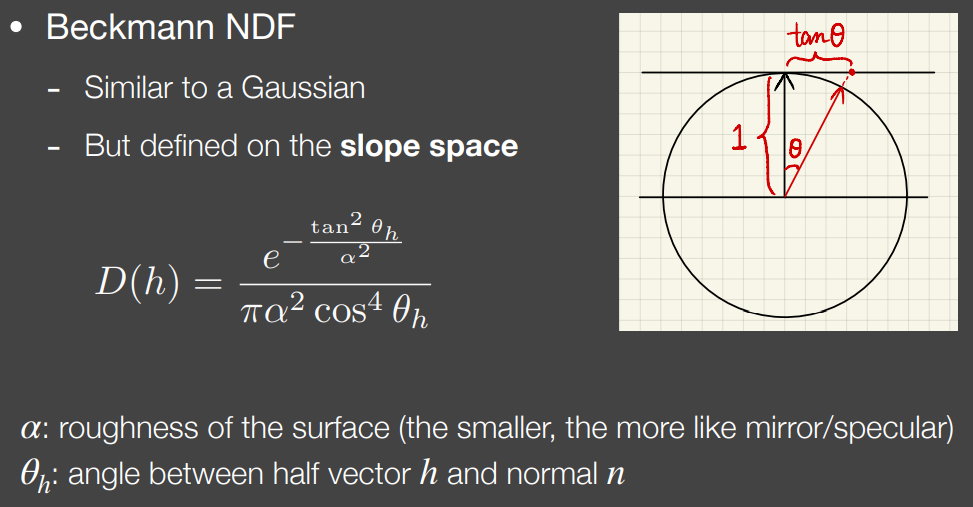
Beckmann NDF

beckmann分布中出现$tan\theta_h$是为了将变量定义在slope space（斜坡空间）

二维情况下，slope space即在单位圆上作水平切线，$\theta$与$tan\theta$关系如图中所示

在高斯分布中，变量直到无穷大函数值不为0（趋近于0），而此处可以将$\theta$限制在90度内（是否需要大于0？），$tan\theta$依然可以取值到无穷大（类似于在$tan\theta$上定义高斯分布，具体是否如此尚未研究），避免出现微表面法线h朝向下方的情况。

分母是为了进行归一化（？）

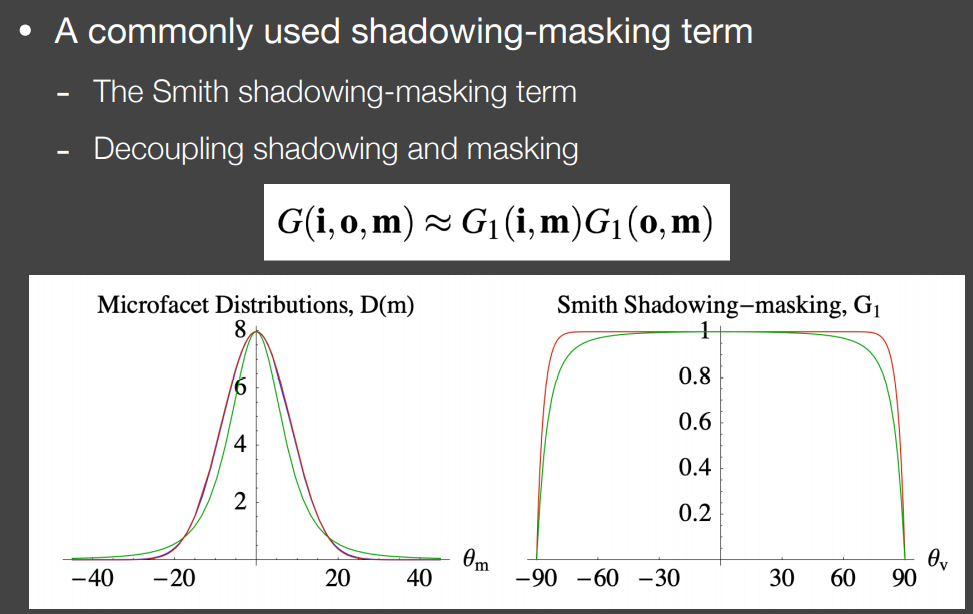
Shadowing-Masking Term

几何项（Shadowing-Masking Term）的意义在于当入射光线与法线接近垂直时（也被叫做grazing angle，比如图中人眼看物体边缘时），BRDF中分子上Fresnel项接近1且分母上$n\cdot i$接近于0，则BRDF接近于极大值，使得渲染后亮度极高，不真实

引入几何项进行一定程度的衰减，其值会在接近grazing angle时趋近于0

The Kulla-Conty Approximation

图中从左到右，BRDF的粗糙度越高，亮度越暗，其中有能量的损失

能量损失的原因在于当粗糙度越高时，法线分布越杂乱，几何遮蔽项G中考虑的光线被微表面遮挡的情况越多。光线被遮挡时本应发生多次反射（bounces）而不是直接被吸收消失，故造成能量损失

一个基本的解决思路是将损失的能量以某种BRDF补全，The Kulla-Conty Approximation是针对该问题的一个近似解决。

图中$E(\mu_o)$计算的是当接收所有方向均匀射入的单位为1radiance的光时，朝$\mu_o$方向射出的radiance，该值在0到1之间，用于衡量能量损失（无损失应为1，此处尚不完全理解，但考虑到BRDF的交换性，该值应与下述$E(\mu_i)$相等，而$E(\mu_i)$较好理解，由此也可解释$E(\mu_o)$值的范围）

同理可也计算$E(\mu_i)$，利用BRDF交换性，其值与同参数大小的$E(\mu_o)$相等，但物理意义可解释为对$\mu_i$方向射入1单位的radiance，向所有方向射出的radiance总和，其值自然为0到1之间，代表能量被反射的比例

图中为了弥补能量损失，增加的BRDF在同样进行E函数的计算后，值应为$1-E(\mu_o)$和$1-E(\mu_i)$，为了构造出具有这种性质的BRDF，设其形式为最简单的$c(1-E(\mu_i))(1-E(\mu_o))$（此处的形式没有具体物理意义，是为了构造具有上述性质的BRDF采取的简单形式）

构造出的具体BRDF及其推导验证如下

由于E的计算没有简单的解析解，但其函数值仅依赖于$\mu$和roughness两个参数，故采用预计算的方法，打表成二维纹理，如下

补充能量损失后的结果如下

但在有颜色情况下，首先发生代表颜色部分的应该存在的能量损失，颜色部分由Fresnel项的平均值决定，具体计算见下图红框

结合之前的E项平均值（此处可理解为经过一次反射后被人眼看到的部分），可以得出经过多次弹射后可见的颜色部分的能量比例，全部求和（似乎是等比数列求和），得到颜色项，使用该项时直接乘以无颜色情况下的补充能量损失的BRDF

结果如下

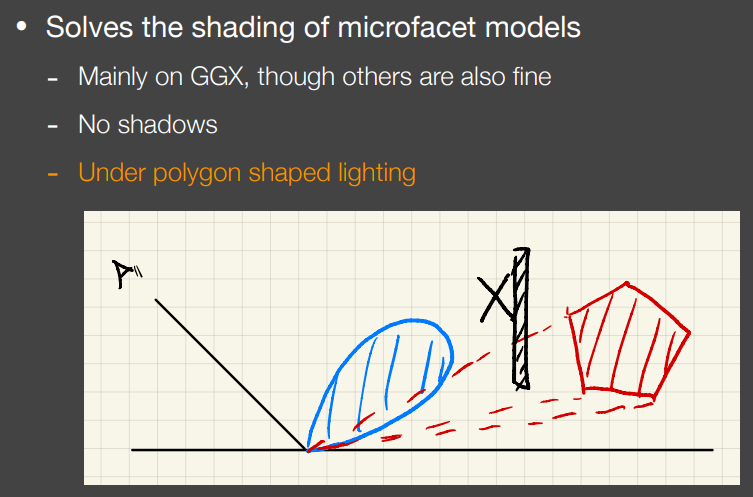
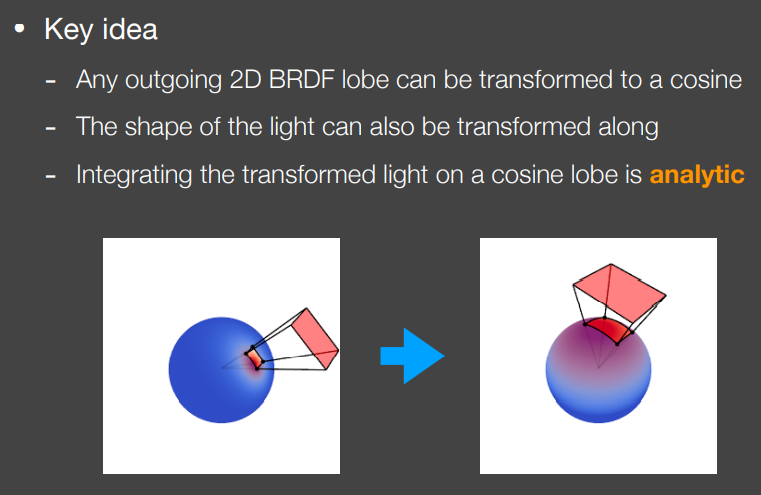
Linearly Transformed Cosines (LTC)

用来解决多边形光源对微表面BRDF模型的着色，不考虑阴影

关键思路

将所有形状的出射BRDF转变为cosine函数

对多边形光源进行同样的转变

在转变后的BRDF lobe上对转变后的多边形光源积分有解析解，便于得到解析解即为主要目的

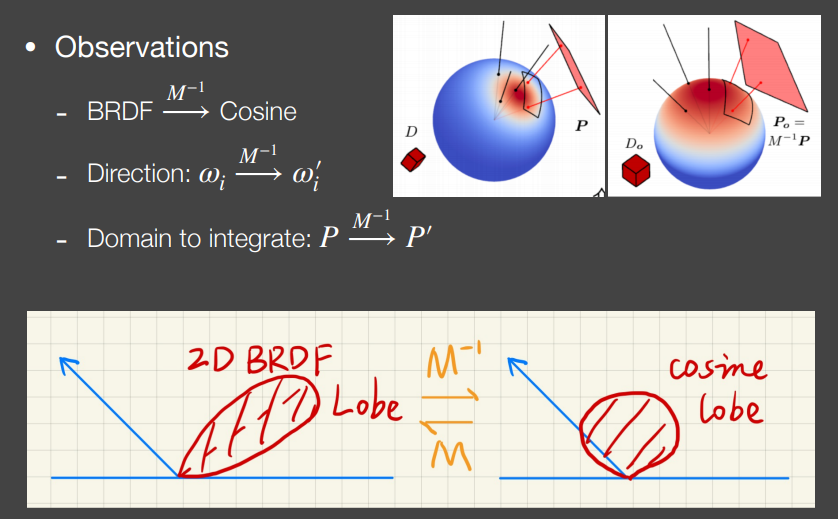
M为cosine到任意BRDF lobe的转换（注意是目标形式到原始形式的转换）

本质上是对渲染方程中的积分做了关于$\omega_i$的变量替换

图中$L_i$可以提取出，因为做了如下假设：多边形光源上任意点到着色点入射的radiance相同

图中J似乎是微积分中的雅可比（有待研究）

结果如下

Disney’s Principled BRDF

主要是为了便于艺术家创作而设计出的BRDF模型

设计原则如下

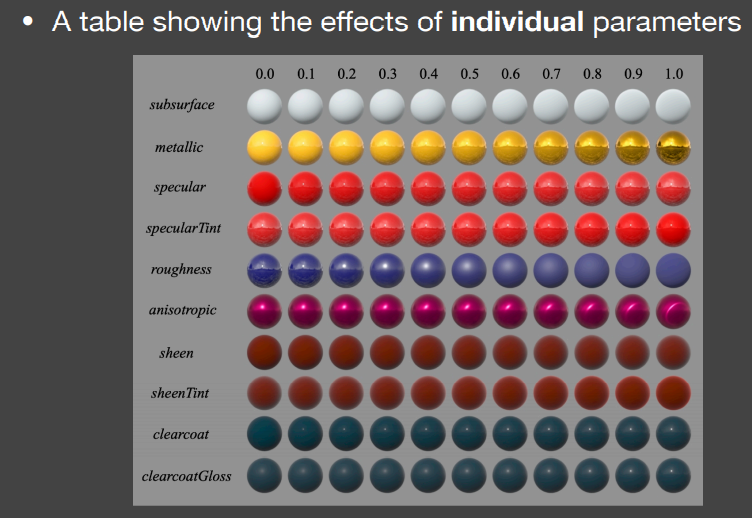
各项参数及其效果如下