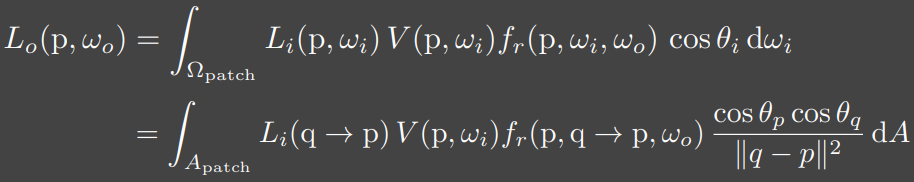全局光照=直接光照+间接光照

直接光照是由光源直接照亮

间接光照是由其他物体表面反射的光照亮

实时渲染中，全局光照一般只解决一次反射的间接光照

Reflective Shadow Maps (RSM)

确定次级光源

首先由经典的shadow map得到光源直接点亮的表面片，作为次级光源（shadow map上每一个像素都是一个表面片patch）

计算次级光源贡献

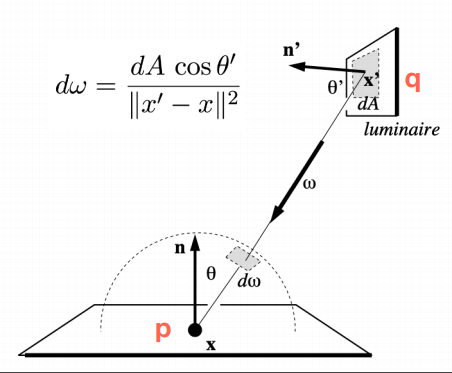
q点为次级光源位置，p点为被照亮的着色点，$\mathrm dA $为像素覆盖的表面片面积，$\mathrm d\omega$为$\mathrm dA $覆盖的立体角。

q对p的光照贡献为对立体角的积分，可转化为表面面积的积分，如上图中公式所示

转化为对表面积的积分后，对应渲染方程的推导如下

渲染方程中$L_i$是q到p的radiance，$V$暂不考虑，假设无遮挡关系（若对每个次级光源考虑对每个着色点的可见性开销太大），$f_r$为着色点的BRDF，可为任意类型（只假设q处为diffuse）

着重考虑$L_i$项，即q点出射的radiance，此处BRDF为diffuse，可得如下关系

$\frac{\phi}{\mathrm dA}$为q点irradiance，乘以BRDF得出射radiance即$L_i$，将$L_i$代入原渲染方程，$\mathrm dA$抵消，剩下BRDF与$\phi$相乘，BRDF为常值，$\phi$由光源决定，在生成shadow map时可储存

并非所有的次级光源都产生贡献，比如被遮挡的（此处暂不考虑）和世界坐标下距离较远的

可以大胆假设在shadow map上距离着色点较远的像素在世界坐标下也距离较远，之后可以通过shadow map上的采样来决定产生贡献的像素（具体采样方法未详细介绍）

下图为需要保存的数据

优势与劣势

优势：

便于实现

劣势：

开销线性相关于光源数

没有间接光照的可见性检测

过多假设，如次级光源为diffuse的表面，shadow map为深度信息却被认为表示距离远近

采样的速度及质量的两难问题

Light Propagation Volumes (LPV)

主要思想是将场景划分为三维网格，在网格中计算间接光的传播

算法流程

step1：生成次级光源

利用RSM即可找到被光源直接点亮的表面，作为次级光源

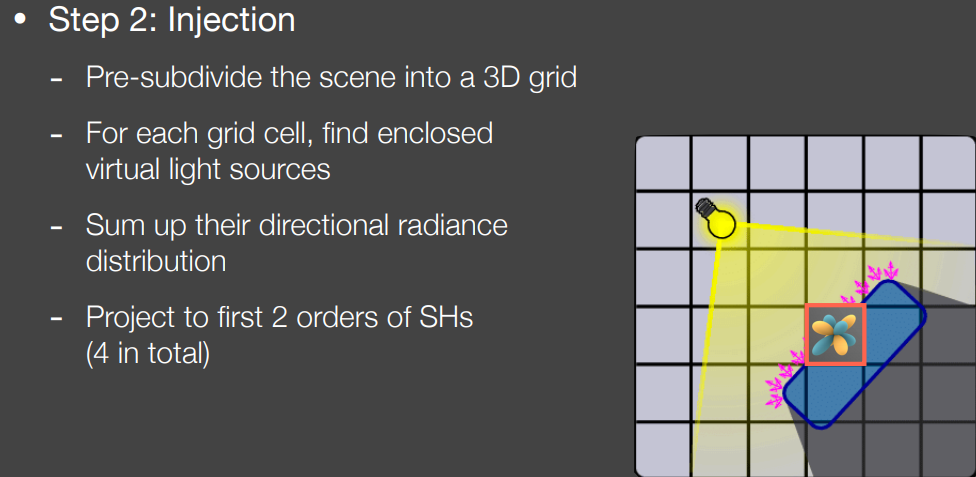
step2：注入次级光源

将场景划分为三维网格

对每一网格，计算所包围的次级光源向各个方向发出的radiance，整体投影到球谐函数SH进行拟合，视为该网格包含的radiance

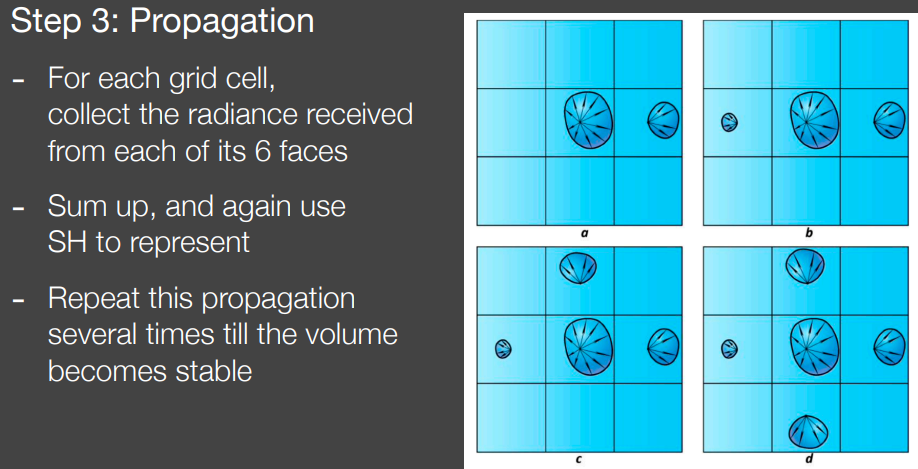
step3：传播

对每个网格，收集从周围六个面传播来的radiance

收集的radiance同样用SH拟合

重复上述过程直到收敛

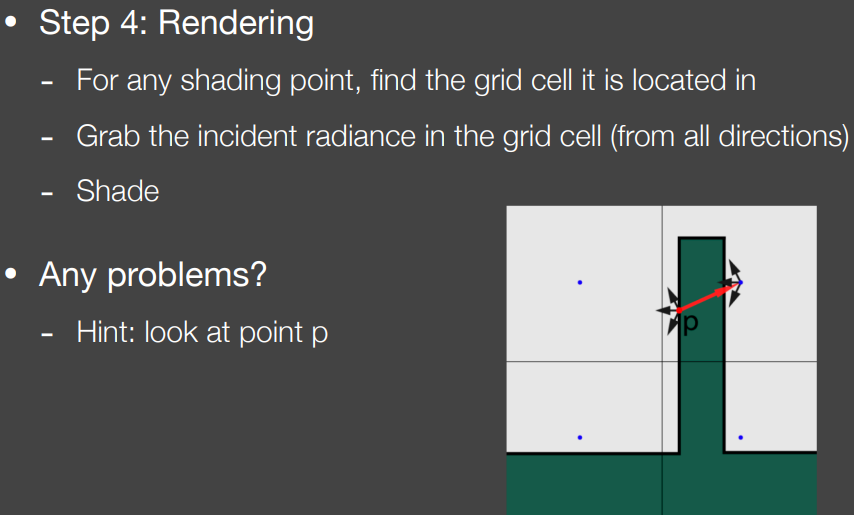
step4：渲染着色点

确定着色点所在的网格

利用该网格所保存的radiance进行着色

可能出现的问题

在step4中，当物体的几何尺度小于网格大小，则会出现网格内部的几何遮挡，即本应被遮蔽的间接光依然被视作可以照亮同网格内的着色点。

这个问题会导致漏光现象（Light leaking），如下图中的屋檐下方

Voxel Global Illumination (VXGI)

将整个场景体素化（Voxelize）并且建立层级结构（hierarchy）

算法流程

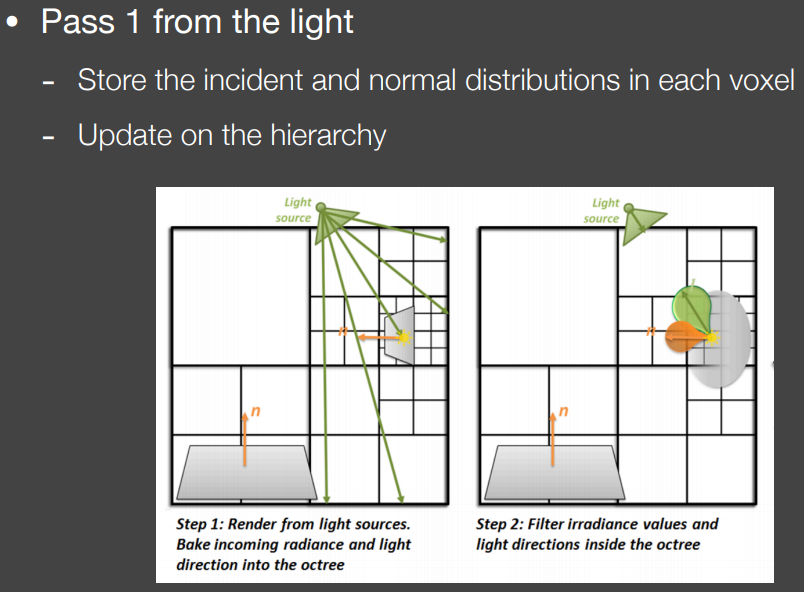
pass1 光源视角下

存储每个体素的入射方向分布和法线方向分布（应当还有入射的radiance），并更新层级结构

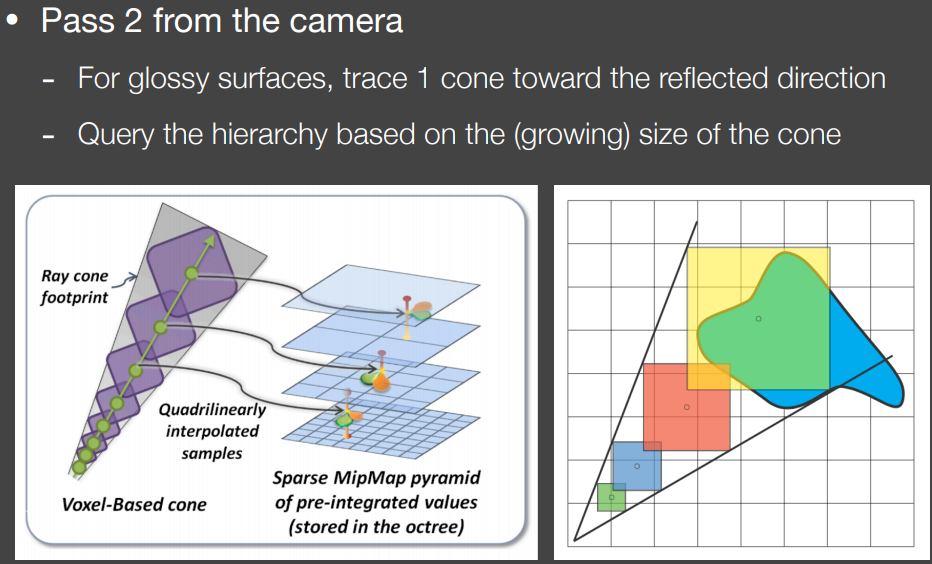
pass2 相机视角下

对glossy的表面，往反射方向追踪一个圆锥体（cone）

追踪圆锥体的过程中逐渐增大在层级结构中的查询尺寸

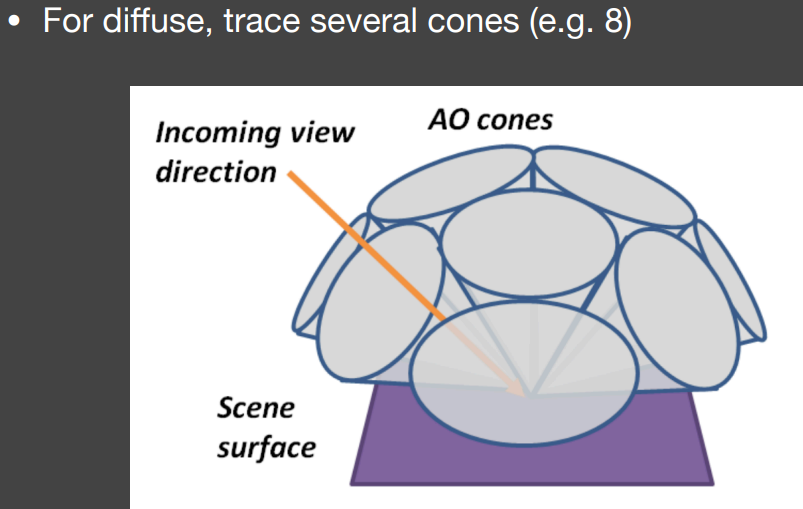
如果是diffuse的表面，可追踪多个圆锥，大体覆盖所有方向，如下图

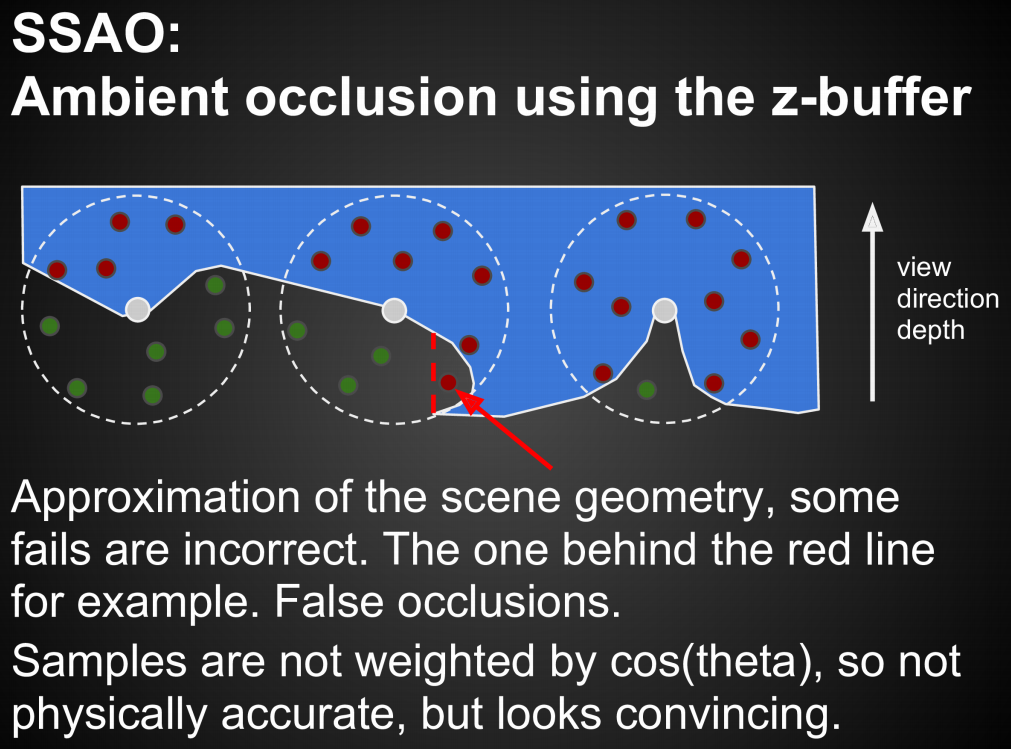
Screen Space Ambient Occlusion (SSAO)

环境光遮蔽（AO）开销小但能强化位置的相对关系

SSAO是对全局光照的一个近似，在屏幕空间中进行

假设间接光照为常数，材质为diffuse

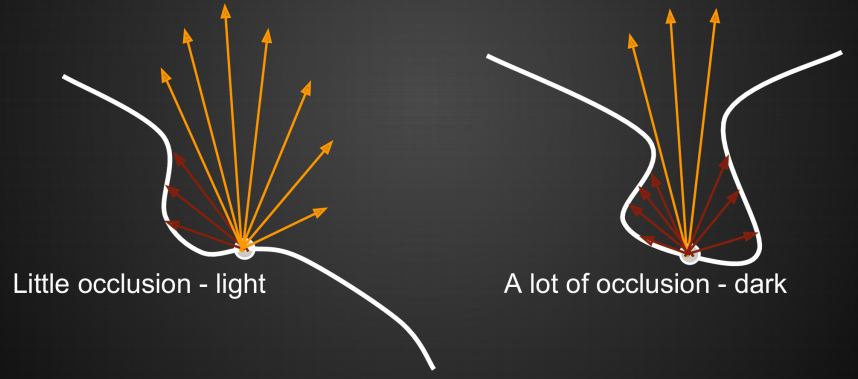
需要考虑着色点处在所有方向上的可见性

受遮蔽少的更亮，受遮蔽多的更暗

数学推导

依然从渲染方程开始，利用乘积积分的一个近似方法进行推导

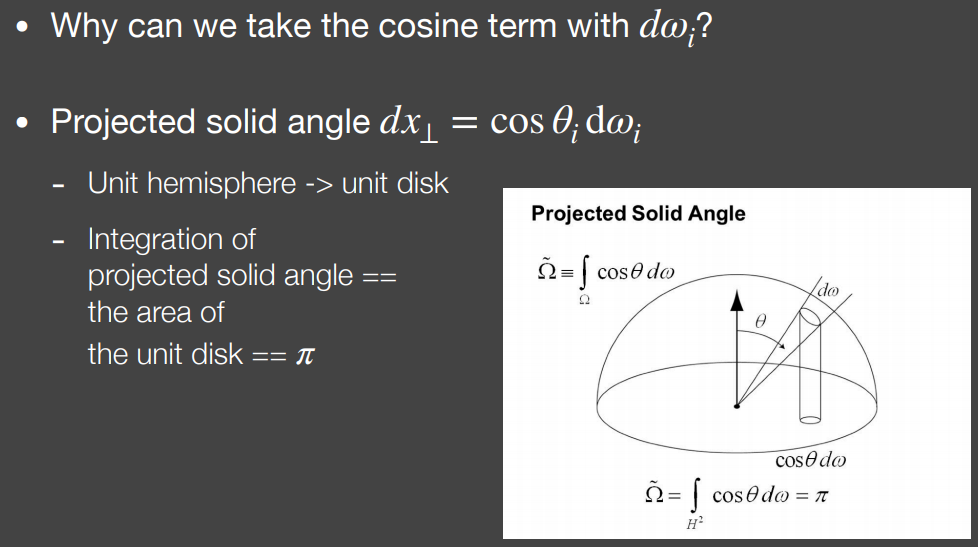
套用近似约等式时，将$cos\theta_i\,\mathrm{d}\omega_i$作为积分变量，得到上图中形式（加入cos目的不明，但使用加入cos的积分变量进行近似时，由于L项和BRDF项均为常数，故该近似实际上是准确的）

$cos\theta_i\,\mathrm{d}\omega_i$的实际意义是立体角在单位圆上的投影，易求得分母下方积分为$\pi$

V项积分变成加权平均，L项积分由于假设间接光照为常数且BRDF为diffuse，推导后依然为常数

更简单直接的推导如下，直接代入常数项即可

计算可见性

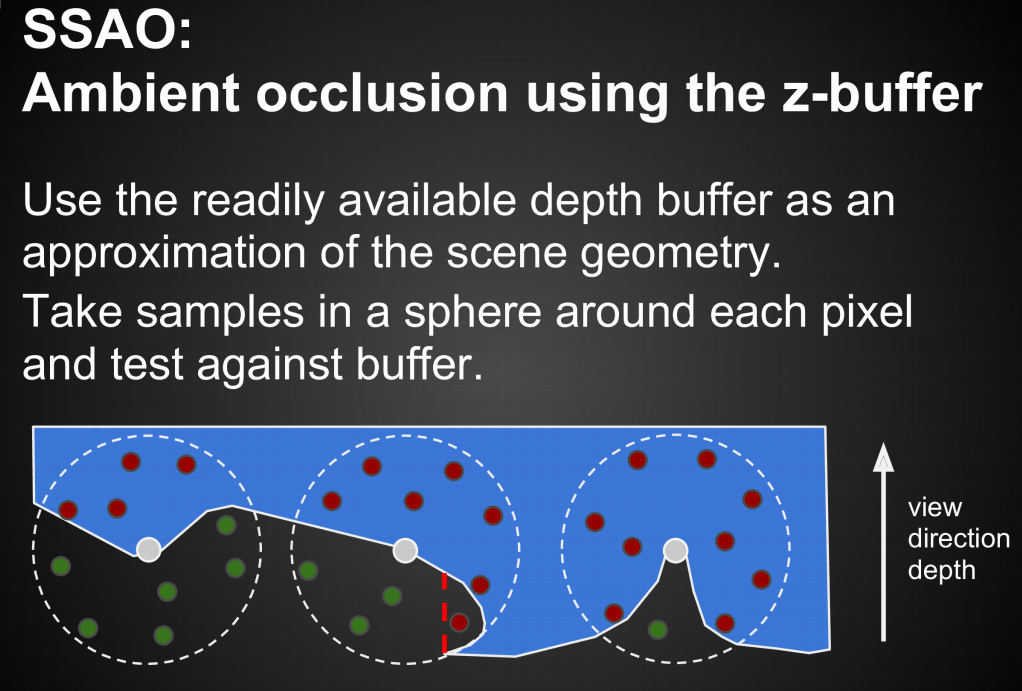
SSAO中使用深度缓冲（z-buffer）来计算可见性

在球形范围内采样点，在深度缓冲中构成遮挡则视作对着色点构成遮挡（即屏幕空间下，人眼看去被遮挡的采样点被认为对着色点构成遮挡，本质是用易于获得的屏幕空间下的深度缓冲信息近似场景中的几何信息）

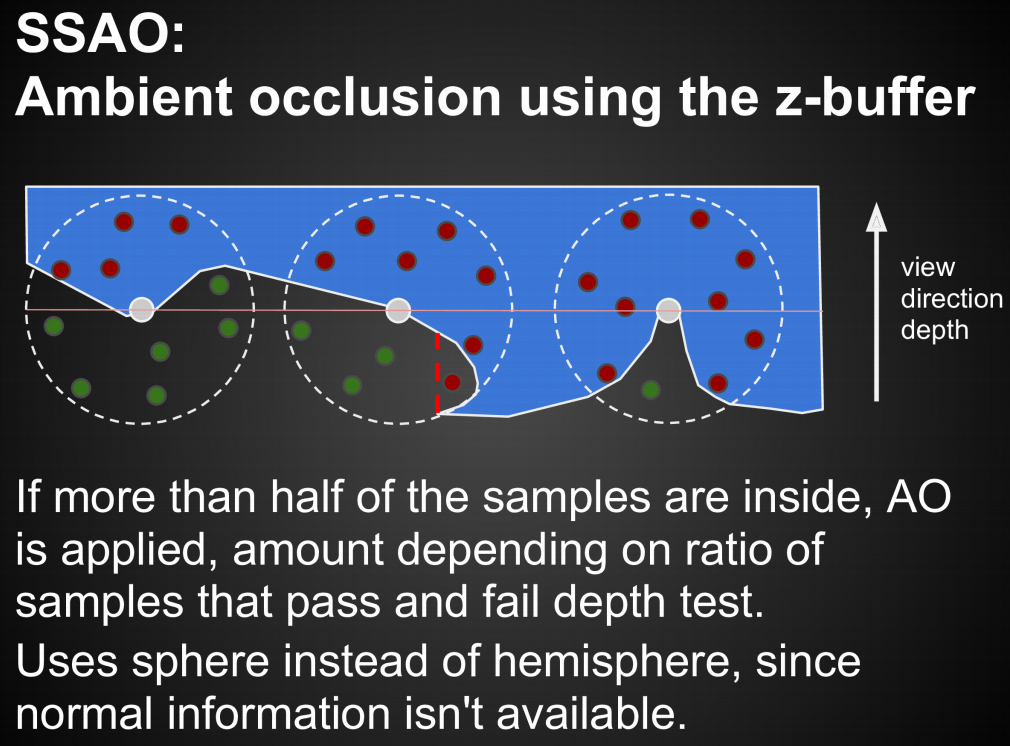
由于理论上只有半球面内的遮挡需要考虑，所以整个球体内，当构成遮挡的采样点超过一半时才视为存在环境光遮蔽（不直接使用半球面的原因是可能没有保存法线信息）

用深度信息近似会产生一些错误，如图中红线内的采样点，实际并未造成遮挡

在数学推导中，对可见性的cos加权在此也没有考虑，因此在物理意义也不准确

SSAO用深度信息近似造成错误遮挡的情形如下

选取采样点计算时一些其他注意事项

为了效率使用较少的采样点，由此产生带噪声的结果，进行模糊处理后，也能得到不错的效果

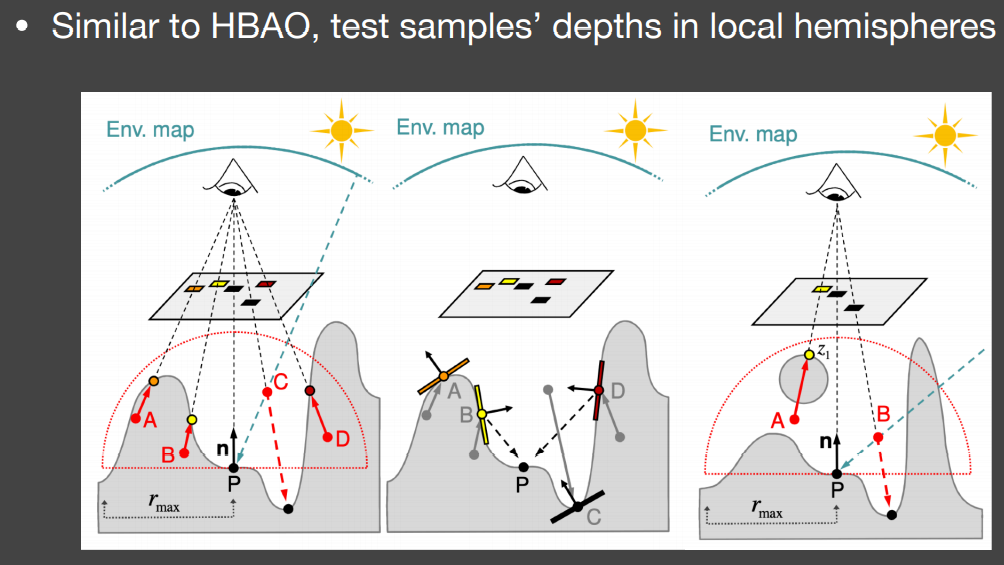
Horizon based ambient occlusion（HBAO）

同样在屏幕空间下，但需要法线已知，仅在半球面内采样，可以减少一些错误。与SSAO的效果对比如下

Screen Space Directional Occlusion (SSDO)

基本思想

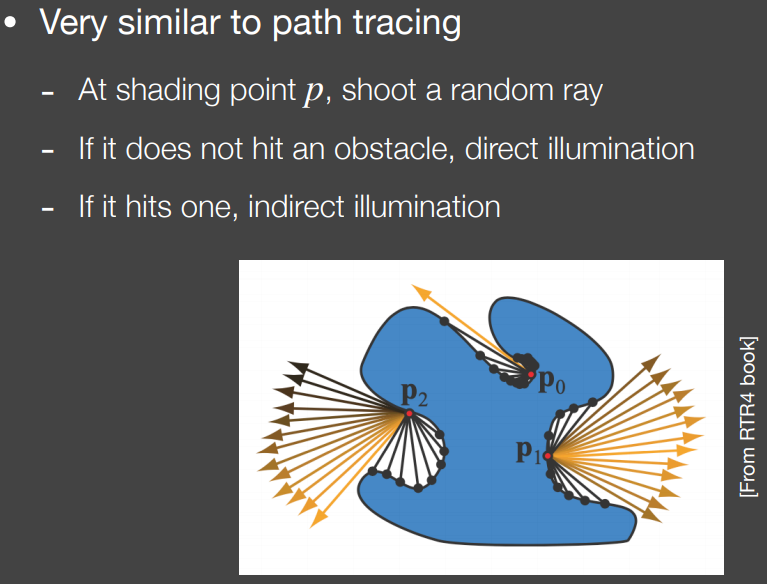
不再假设间接光照为常数，而是考虑一部分真实的间接光照，但是次级光源在屏幕空间下

基本思想类似于path tracing，如下

在着色点附近，若某方向上存在遮挡，即射线与物体表面相交，则视为接收到交点处反射来的间接光；若某方向上没有遮挡，则视为接收到外部的直接光

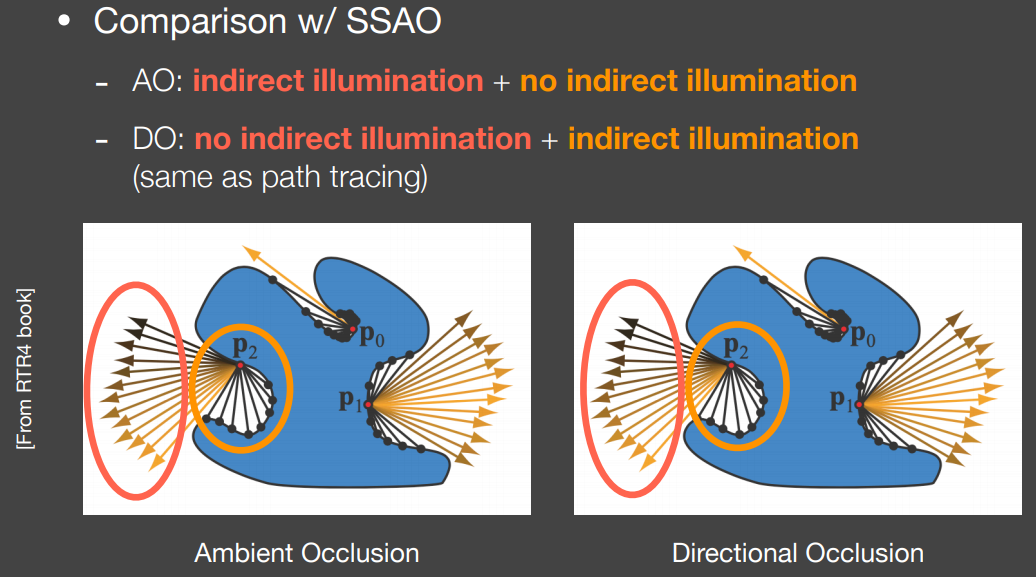
基本思想恰好与SSAO相反

SSAO中，着色点附近有遮挡则视为无间接光。两种方法思路相反的根本原因在于SSAO只考虑来自远处的间接光，而SSDO只考虑来自近处的间接光

（个人理解：SSDO只考虑近处的间接光，而间接光本应对近处的着色点有较多贡献，更加合理）

简单的数学描述如下

算法简介

与HBAO类似，同样是在已知法线的情况下，在半球面内采样点，采样点到着色点是否存在遮挡由屏幕空间下采样点的可见性决定，被认为到着色点无遮挡的采样点视作无间接光，转而接收该方向上的来自外部的直接光（图左侧）

每个采样点在屏幕空间下对应一个次级光源，被认为到着色点有遮挡的采样点（即屏幕空间下不可见的）对应的次级光源才对着色点有光照贡献，不过当着色点在次级光源面片的法线背面时，光照贡献为0（图中间）

可能存在的问题依然是将屏幕空间的深度信息视作场景中的几何信息可能会出现的错误，比如采样点到着色点实际无遮挡，但因为屏幕空间下不可见而被认为有遮挡；又或者被认为无遮挡的采样点，在该方向远处的直接光实际上是被遮挡的（图右侧）

存在的问题

虽然质量不错，但只利用屏幕空间信息会忽略不可见的表面

比如图中，地面上本应有来自黄色表面的间接光照，但在黄色表面逐渐转向不可见的一侧时，因为屏幕空间下对应的次级光源只能是可见的侧面，故不会对原来地面上的位置有光照贡献。这可能也是所有屏幕空间方法的问题

另外一个问题是SSDO只考虑小范围内的间接光

比如图中立方体侧面应该接受来自绿色墙体的间接光，若是SSDO方法则可能不会考虑到较远距离的绿色墙体

Screen Space Reflection (SSR)

本质是在屏幕空间下做ray tracing

效果如下

用SSR做基本的镜面反射，大概流程如下

ray tracing过程

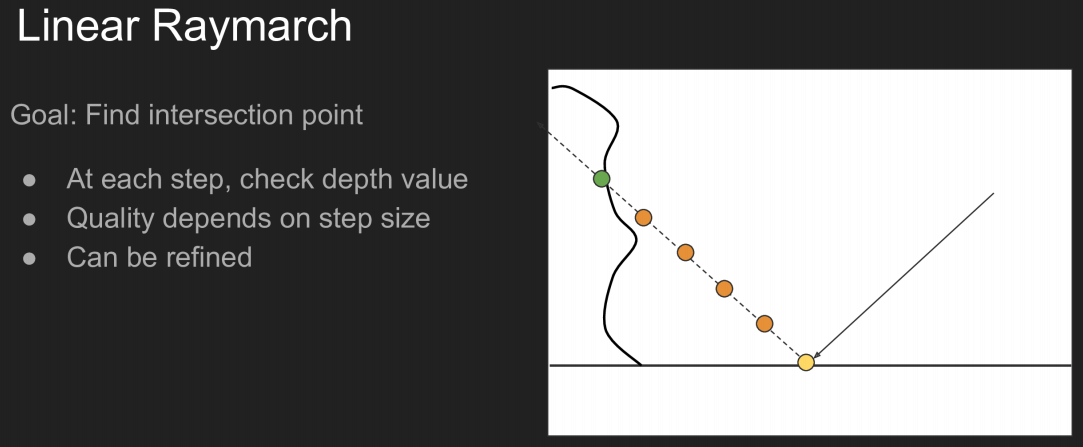
在着色点处追踪光线时，运用raymarch的方法，如下

基本思路是光线以固定值步进（后续加入层次结构以变化步长前进），每一步检查深度值，若在屏幕空间下被遮蔽，则与物体表面相交

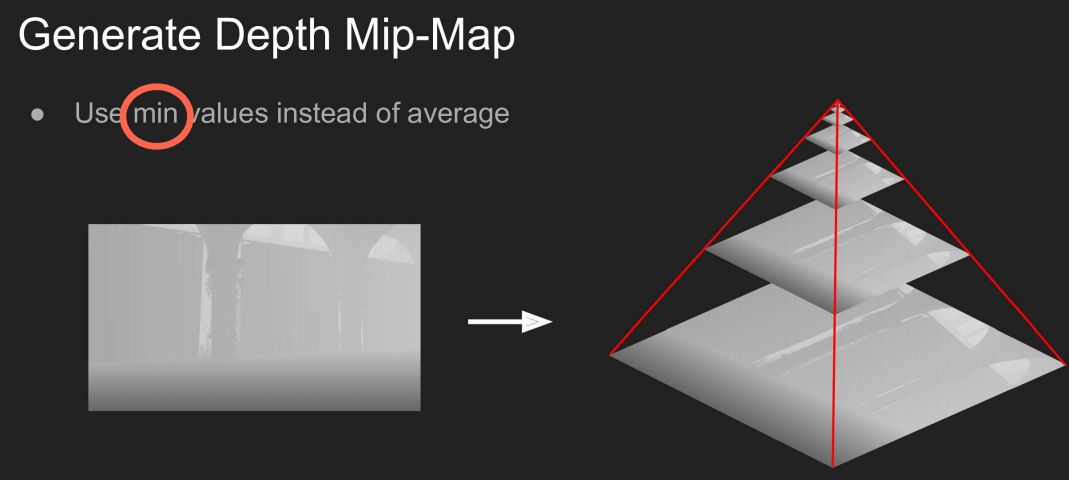
加入层次结构加速raymarch过程，先由屏幕空间深度图生成mipmap，此处mipmap不再是用均值压缩，而是用最小值

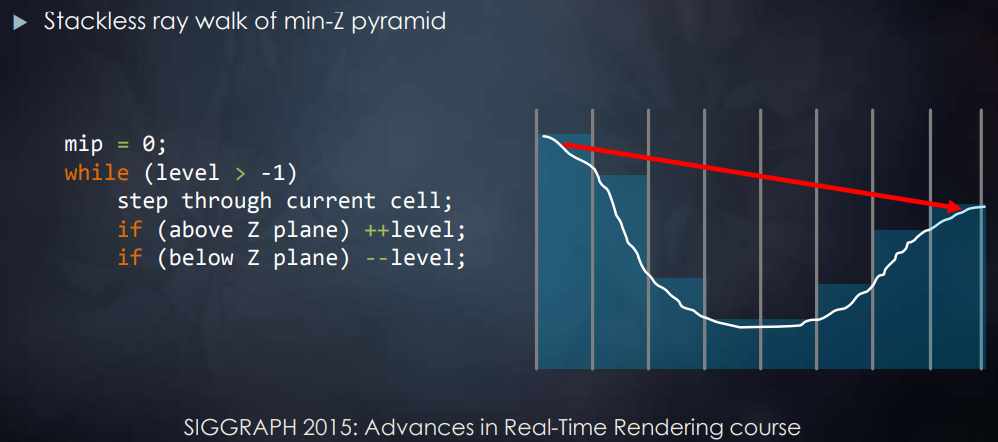
利用层次结构进行raymarch的具体算法如下

第一步在mip0层步进，若不相交则层数加一，如此不断扩大步长直到相交，相交后不再步进，缩小mip层次，确定mip0层的相交位置即为所求。

着色

同样需要假设次级光源为diffuse的表面，因为只有屏幕空间信息，相当于只知道相机方向的radiance，只有作diffuse假设才能认为到着色点方向的radiance已知

能达到的效果

清晰或模糊的反射

离物体近的表面接收的反射更加清晰，因为以圆锥状向外追踪多条光线时，距离较近则采样光线较集中于小范围

对各向同性表面，由于BRDF形状为椭圆，故反射景象有所拉长（此处尚不理解）

接收反射的表面可以有各处不相同的粗糙度和法向

光线追踪改进思路

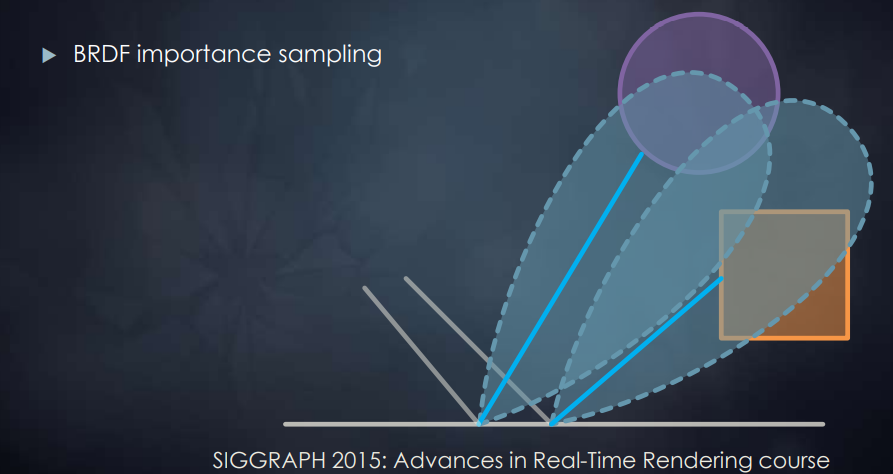
根据BRDF性质的重要性采样

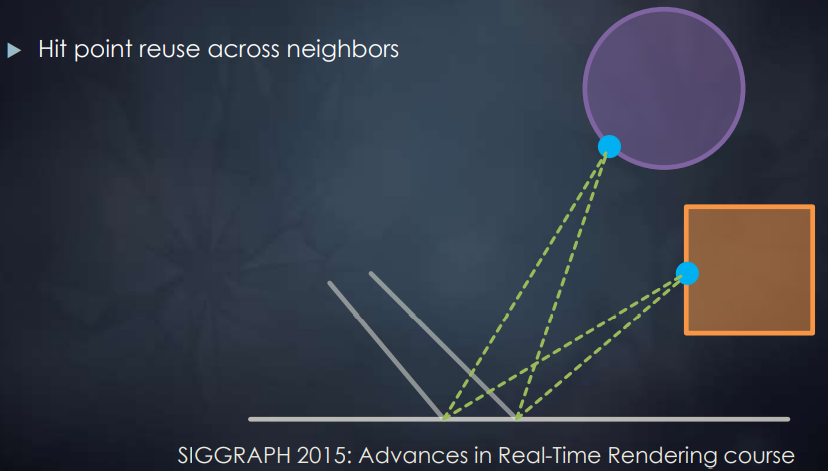
复用周围点的采样光线，因为两点的采样光线都可能打在同样的交点处

提前将结果滤波，只需查询镜面反射方向的结构

存在的问题

只有屏幕空间信息相当于只能看见物体的外壳

屏幕空间外的物体自然也不会追踪到，但可以通过边缘模糊实现类似淡出的效果，缓解该问题的影响

优缺点的简单总结