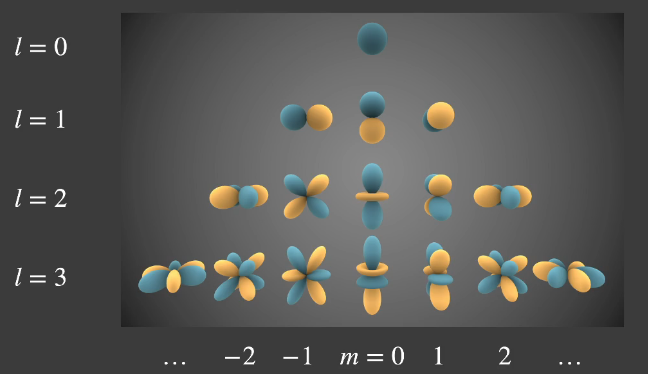Approximation in RTR

本节用到的一个数学近似。

有很多不等式，在一定情况下可以看作等号成立。由于实时渲染只要求看着真实，而不必满足绝对的真实，因此这种近似可以应用在渲染方程中。
$$
\int_{\Omega}f(x)g(x)dx \approx \frac{\int_{\Omega}f(x)dx}{\int_{\Omega}dx} \cdot \int_{\Omega}g(x)dx \tag{1}
$$
(数学含义或者证明待补充)

当满足以下其中一个条件时，两边可近似相等

1. Small support

   指的是公式中的积分域 $\Omega$ 尽可能小的时候。因此如果只考虑直接光照，在点光源和方向光源的情况下， $\Omega$ 就只表示光源方向的立体角，就会很小，如果考虑一个点的镜面反射，则渲染方程中的 $\Omega$ 就只是镜面反射方向上的很小的立体角。

2. Smooth integrand

   指的是被积函数 $g(x)$ 在 $\Omega$ 内的变化很小，即频率低，“光滑”的情况下。因此如果G(x)是一个漫反射的BRDF，那么它值的变化就不大。

当满足上面其中一个条件时，对于渲染方程来说，把 $V()$ 看作 $f(x)$ ,其他项看作 $g(x)$，渲染方程就可以写成：
$$
L_0(p,w_0) \approx \frac{\int_{\Omega^+}V(p,w_i) dw_i}{\int_{\Omega^+}dw_i} \cdot \int_{\Omega^+} L_i(p,w_i) f_r(p,w_i,w_o) cos\theta_i dw_i \tag{2}
$$

IBL(Image Based Lighting)

IBL，使用一张图像来，表示所有方向上的环境光。

一般有两种存储方式，spherical map 和 cube map

Shading : The Split Sum

split sum是一种在环境光下着色的算法。

这里只考虑着色，不考虑阴影。渲染方程里也不考虑visibility项：
$$
L_0(p,w_0) = \int_{\Omega^+} L_i(p,w_i) f_r(p,w_i,w_o) cos\theta_i dw_i \tag{3}
$$
解此方程可用蒙特卡洛积分采样，但实时渲染希望避免采样带来的耗费，于是可以使本文开头的数学近似。

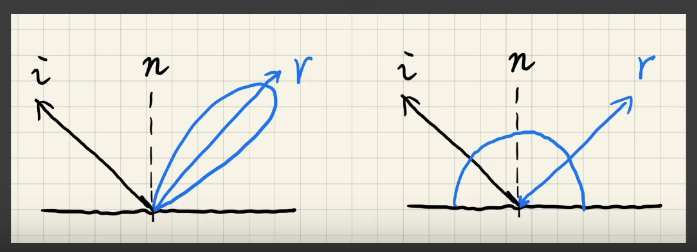
如果brdf是glossy的（左图），那么积分域就很小；如果brdf是diffuse的（右图），那么brdf的值变化就不大。因此可以使用公式（1）将公式（3）近似为：
$$
L_0(p,w_0) \approx \frac{\int_{\Omega_{fr}}L_i(p,w_i) dw_i}{\int_{\Omega_{fr}}dw_i} \cdot \int_{\Omega^+} f_r(p,w_i,w_o) cos\theta_i dw_i \tag{4}
$$
考虑左边的项$\frac{\int_{\Omega_{fr}}L_i(p,w_i) dw_i}{\int_{\Omega_{fr}}dw_i} $，对光源的积分再除以对1的积分，对离散值来说就是加权平均，也就相当于对环境光的图像做了一个高斯滤波，这些滤波图像是可以预计算的：

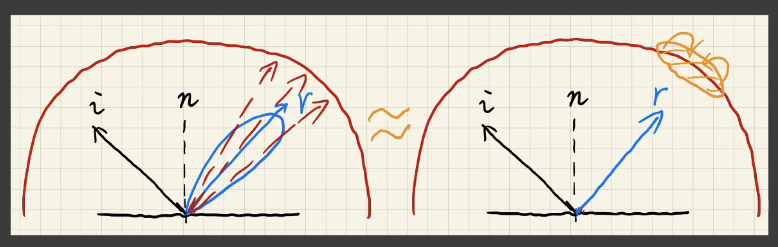
而原理也可以直观地进行理解：

对于一个glossy的材质，渲染方程中是对它的lobe的立体角内进行采样（左图），每个方向采样的概率不同，所以结果就近似于在lobe内所有方向上的值的加权平均（右图）。

到这里，对于公式（4），左边的项$\frac{\int_{\Omega_{fr}}L_i(p,w_i) dw_i}{\int_{\Omega_{fr}}dw_i} $已经可以预计算出来了，接下来考虑右边的项：$\int_{\Omega^+} f_r(p,w_i,w_o) cos\theta_i dw_i$ 。

这里涉及微表面反射BRDF以及其中的菲尼尔项等（我都忘光了）。总体来说就是一个将参数降至两维然后打表预计算的思想。

假设BRDF采用的是Microfacet BRDF：
$$
f(i,o) = \frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)} \tag{5}
$$
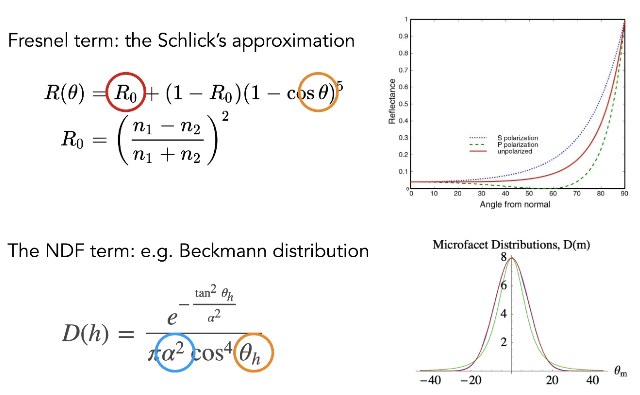
不考虑其中的 $G(i,o,h)$ 即shadowing-masking 项，那么还剩菲涅}尔项和法线分布函数项。

总结下：对于一个着色点 $p$，积分$\int_{\Omega^+} f_r(p,w_i,w_o) cos\theta_i dw_i$ 中只含有三个变量：基础反射率 $R_0$（表示颜色），入射角 $\theta$，粗糙程度 $\alpha$。然而三维的表还是太大了。

根据公式（5），对此积分公式进行化简，提取出 $R_0$，对于一个特定的BRDF， $R_0$是确定的，因此只需要对剩余两个参数打一个表，预计算出下面公式右边的两个积分值。整个积分的求值就只需要查两次表。
$$
\int_{\Omega^+} f_r(p,w_i,w_o) cos\theta_i dw_i \approx R_0 \int_{\Omega^+} \frac{f_r}{F}(1-(1-cos\theta_{i})^5) cos\theta_i dw_i + \int_{\Omega^+} \frac{f_r}{F}(1-cos\theta_{i})^5 cos\theta_i dw_i \tag{6}
$$
整个split sum过程就完成了，通过多处预计算，不需要进行采样，可以直接求出着色点颜色。

Shadow from environment lighting

环境光的阴影很难做，有多种解决办法，包括

1. 把此问题看作多光源阴影问题（复杂度线性于光源数量）。
2. 把此问题看作采样问题（Visibility项非常复杂，且不能从环境中很好的分离出来）。
3. 工业界做法，用一个最主要的光源生成阴影。

本节算法 Precomputed radiance trasfer。

Spherical Harmonics

球谐函数，是定义在一个球面上的一组函数，参数维度为两维（$\theta, \phi$）。

图中每一个形状都代表一个基函数，从上到下每一阶表示函数值有不同的频率（类比傅里叶函数的基函数），第0阶（$l = 0$）频率最低。环境光其实就是一个在球面上的函数，不同立体角方向上有着不同的值。那么这个函数可以用球谐函数的基函数的线性组合来表示。

对于任意一个二维的函数$f(w)$，它可以用积函数的线性组合来表示，那么对于一个基函数$B_i(w)$，它前面的系数$c_i$，可以通过一个积分求得：
$$
c_i = \int_\Omega f(w)B_i(w)dw \tag{7}
$$
类比三维空间的三个基$[1,0,0],[0,1,0],[0,0,1]$，也可以把他们看作球面上的函数，每个基只在一个立体角方向上有值。那么任意一个三维向量$[x,y,z]$，都可以用这三个基来表示。每个基前面的系数也可以用上面的公式得到，只不过公式里的 $\Omega$ 就只是一个立体角方向，因此结果就是$f(w)B_i(w) = [x,y,z] \cdot [1,0,0] = x$。这个操作可以叫做投影 。

球谐函数有着这样的性质，即都是单位正交基：
$$
\int_{\Omega}B_i(w) \cdot B_j(w)dw = 1 \quad(i = j)\
\int_{\Omega}B_i(w) \cdot B_j(w)dw = 0 \quad(i \neq j) \tag{8}
$$
对于BRDF函数，出射方向（射入人眼的方向）已知的情况下，也可以看作是一个球面上的函数，那么也可以投影到球谐函数上。

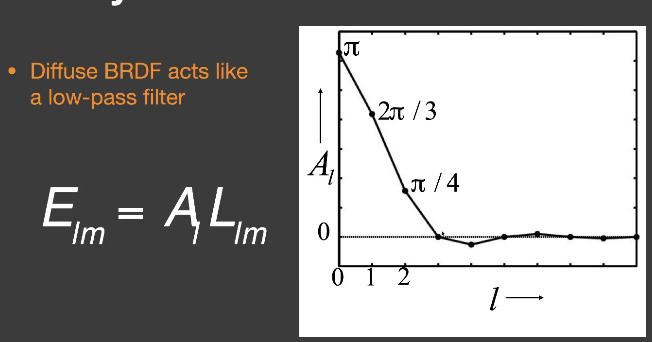
如果将一个diffuse的BRDF函数投影到球谐函数上的话，发现前三阶基函数的系数是有很大值的，而后面阶数的系数就几乎为0，表示diffuse的BRDF是没有什么高频信息的。

而渲染方程是lighting和BRDF的点积的积分，用到上面提到的知识，点积可以看成是投影。不管多高频的lighting，投影到低频的BRDF上，结果仍是低频的。因此对于diffuse的BRDF，如果BRDF只用前三阶基函数就可以表示，那么lighting也只需要三阶。

PRT（Precomputed Radiance Transfer）

基于球谐函数，就可以得到环境光下的阴影，这种着色方法叫做PRT。
$$
L(o) = \int_{\Omega}L(i)V(i)\rho(i,o)max(0,n\cdot i)di \tag{9}
$$

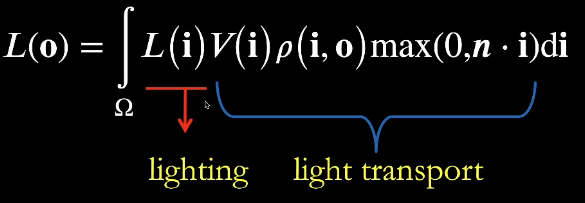
对于上面的渲染方程，若场景中所有物体都不变，观察方向给定，则其中每一项都可以看作是球面上的一个函数，求积分就是将四项的值对应相乘。

把$L(i)$之外的项看作 light transport：

对于Diffuse情况，BRDF值是常数，提到前面，将$L(i)$用基函数的线性组合来表示（预计算），然后交换积分求和顺序，现在积分号里是基函数和light transport的乘积，那么又可以将light transport投影到基函数上（预计算），最终得到的结果只需要计算两个向量的点乘：

这一方法的限制就是：

1. diffuse
2. 场景中所有物体都不动
3. 观察方向不变（diffuse情况下，其实观察方向可以是任意的）

但有一点可以变化，环境光可以旋转，因为环境光旋转后，用来表示它的球谐函数基函数的线性组合也可以很快地得到。