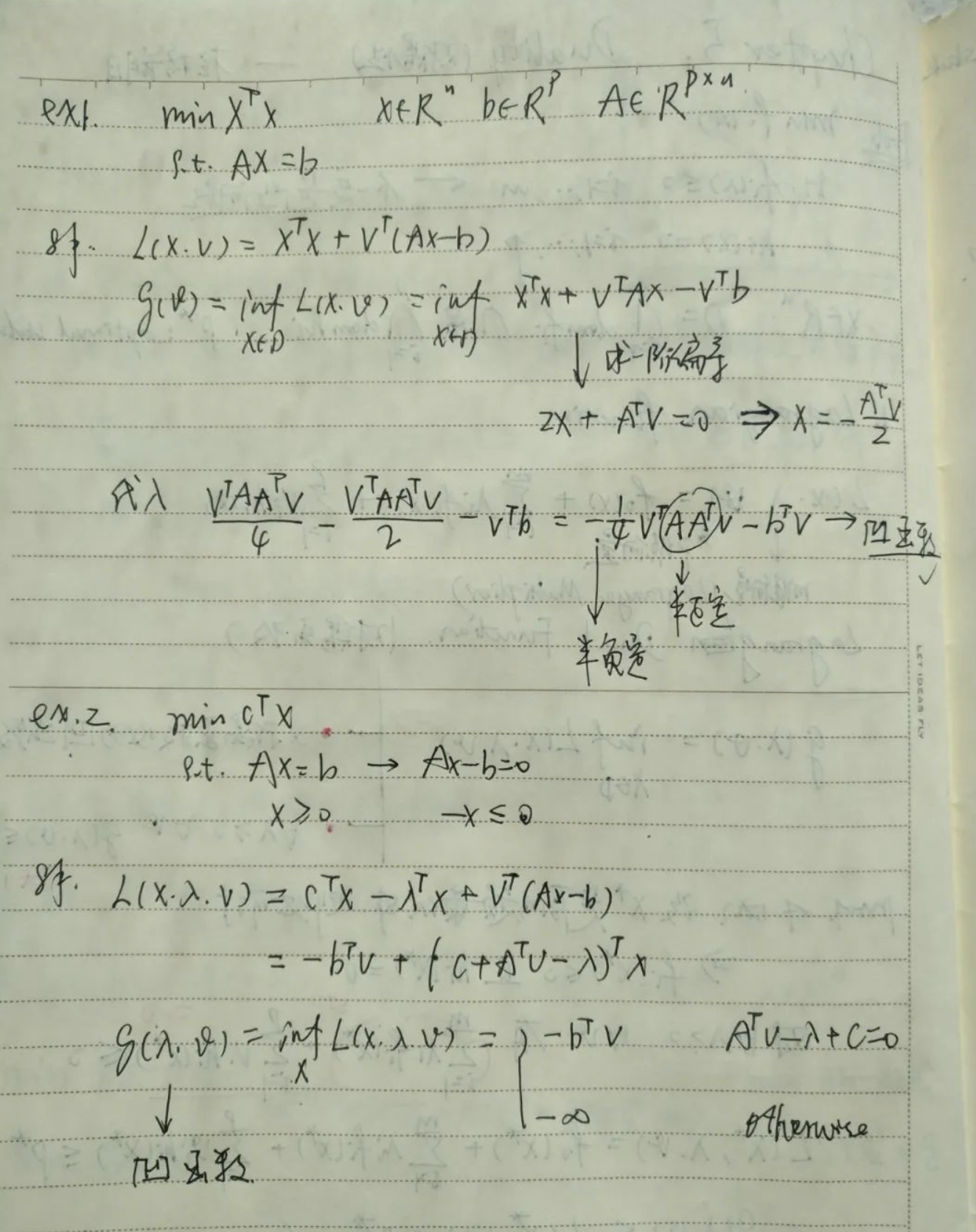Yann
人工智能、计算机、机器学习、linux、程序员
Convex Optimization-6
本节我们先从一般的优化问题出发构造两个函数:
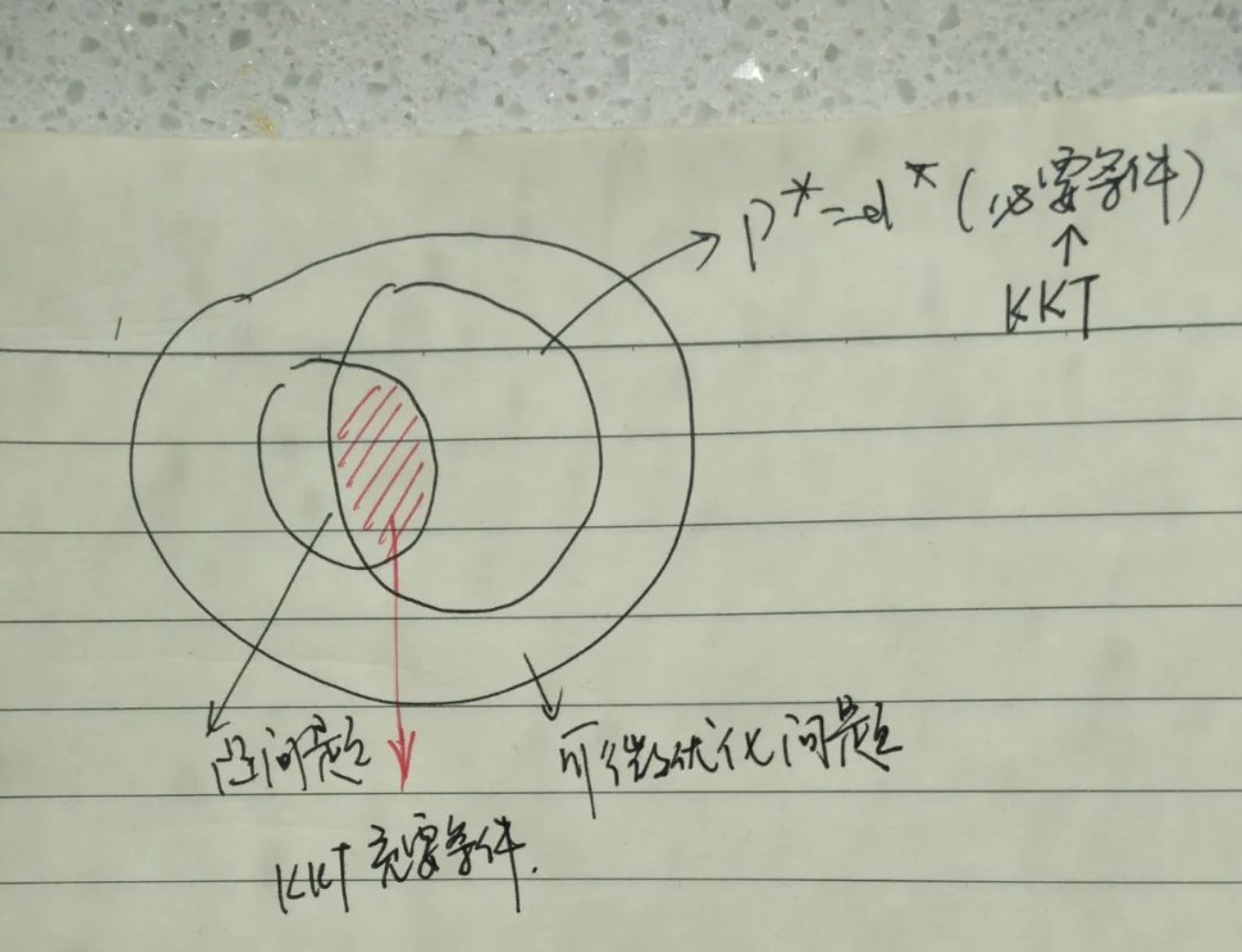
Lagrangian Function和Lagrange Dual Function(我们指出虽然原问题不一定是凸问题,但他的拉格朗日对偶函数一定是凹函数,我们通过一些例子说明了这一情况),我们用几个例子说明了对偶函数与函数的共轭之间的关系。本节的关键是讨论原问题(P)和其对偶问题(D)的性质与关系,我们指出对偶问题一定是凸优化问题,并给出了三个衡量二者关系的指标(弱对偶、强对偶、对偶间隙),问题是什么时候有d*=p*。我们首先给出了等号成立时的三种解释(几何解释、鞍点解释、多目标优化解释),并细致的讨论了鞍点的性质由此推出鞍点定理,在d=p成立的条件下我们得出了5个条件,并在一起称之为KKT条件(Karush Kuhn Tucker),最后我们证明了一条重要的结论:若原问题为凸问题,各个函数可微,对偶间隙为0,则KKT条件为充要条件。
下图清晰地展示了我们本节所做的事情: