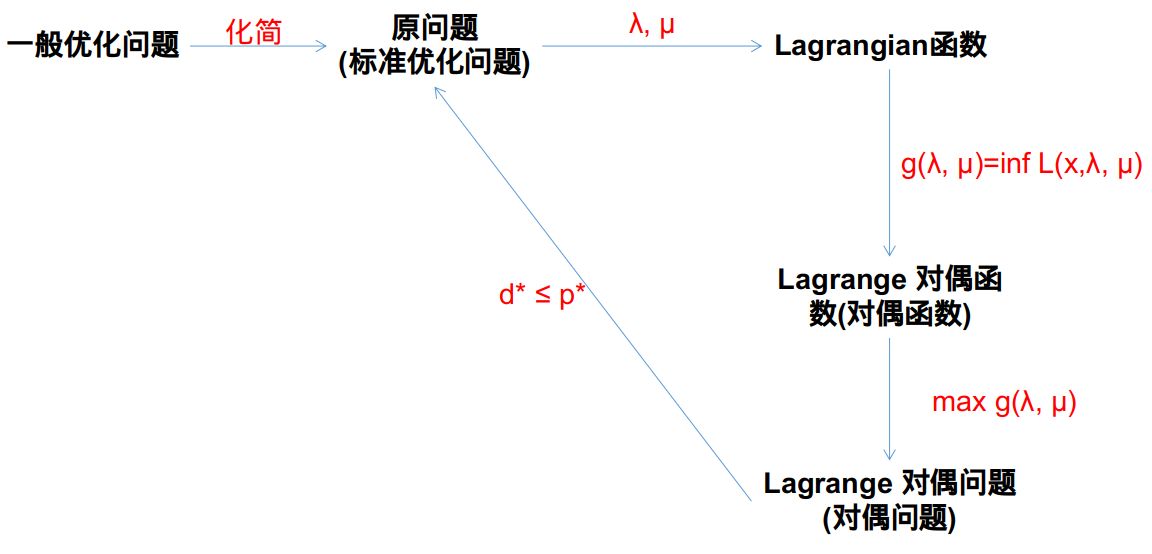
1.前言
在读论文或者学习机器学习理论时,常常看到对偶的身影。但因为对对偶问题的理解不够透彻,在看机器学习理论相关理论时也是懵懵懂懂。所以本文整理了对偶理论的基本概念,帮助理解记忆。本文主要描述:
- 优化问题的标准形式,即原问题的基本定义;
- 介绍 Lagragian 函数,Lagrage 对偶函数/对偶函数,Lagrage 对偶问题/对偶问题等基本概念;
- 介绍将原问题转化为对偶问题的方法;
2.优化问题的标准形式(原问题)
优化问题的形式有很多,如最大化一个目标函数,或者最小化一个目标函数,约束的不等号方向不同等。每一个形式的优化问题,都可以求出相应的对偶问题,但因为优化问题形式的不同,求解细节上,会有相应的不同,很难掌握。为了方便记忆,先定义标准优化问题(原问题),然后再介绍标准优化问题转化为对偶问题的过程。
理论上所有的优化问题,都可以转化为标准形式。优化问题的标准形式如式2-1所示:
$$
\begin{aligned}
\min & f_{0}(x) \
\text { s.t. } & f_{i}(x) \leq 0 \quad i=1, \ldots, m \
& h_{j}(x)=0 \quad j=1, \ldots, p
\end{aligned}
$$
由优化目标, 不等式约束和等式约束三部分组成。式2-1有三个需要额外注意的地方:
- $f_{0}(x)$ 是优化目标, 期望可以最小化的量。它的形式无约束, 可以是凸函数, 也可以是非凸函 数;
- $f_{i}(x)$ 是优化问题的不等式约束,注意符号是“\leq”且不等式右端为 0, 共m 个不等式约束, 可以 是线性不等式, 也可以是非线性不等式;
- $h_{j}$ 是优化问题的等式约束, 且“ $=$ ”右端为 0 , 共有 $\mathrm{p}$ 个等式约束, 可以是线性等式, 也可以是 非线性等式;
其中 $x \in \mathbf{R}^{n}$, 问题的定义域是优化目标与所有约束的交集 $\mathcal{D}=\bigcap_{i=1}^{m} \operatorname{dom} f_{i} \cap f_{0} \cap \bigcap_{j=1}^{\infty} h_{j}(x)$ 。求 解优化问题是在定义域 $\mathcal{D}$ 中寻找到 $x^{}$ 使优化目标 $f_{0}(x)$ 达到最小值 $p^{}$ 。
理论上我们遇到的所有的优化问题都可以化为式2-1这种标准形式。比如我们的优化目标要极大 化 $\max f_{0}(x)$,可以等效为极小化 $\min -f_{0}(x)$ 。同理所有的不等式约束和等式约束经过化简变换 后也可以转化为式2-1中形式。若某些优化问题, 没有不等式约束, 则标准形式中 $f_{i}(x)$ 的数量 为 0 ; 同理若优化问题中没有等式约束, 则对应的标准形式中 $h_{j}(x)$ 的数量为 $0 ;$ 若优化问题 中, 既没有不等式约束也没有等式约束, 则对应的标准形式是一个无约束的优化问题。另外根据 $f_{0}(x), f_{i}(x), h_{j}(x)$ 的形式不同, 优化问题可以分为不同的种类, 难易程度也会有很大的区别。 本文我们主要讨论对偶理论, 对优化问题的种类和难易不做过多的描述, 只要知道任何形式的优 化问题均可以转化为这种标准形式即可。我们通过一个简单案例看看如何将一般优化问题转化为 标准形式:
例 1. 将式2-2转为优化问题的标准形式:
$$
\begin{array}{ll}
\max & -x_{1}+x_{2}+x_{3} \
\text { s.t. } \quad & x_{1}+x_{2}+2 x_{3} \leq 25 \
& -x_{1}+2 x_{2}-x_{3} \geq 2 \
& x_{1}-x_{2}+x_{3}=3 \
& x_{1}, x_{2} \geq 0
\end{array}
$$
转化为标准形式为:
$$
\begin{array}{ll}
\min & x_{1}-x_{2}-x_{3} \
\text { s.t. } & x_{1}+x_{2}+2 x_{3}-25 \leq 0 \
& x_{1}-2 x_{2}+x_{3}+2 \leq 0 \
& -x_{1} \leq 0 \
& -x_{2} \leq 0 \
& x_{1}-x_{2}+x_{3}-3=0
\end{array}
$$
3. Lagragian 函数
根据原问题(优化问题的标准形式),我们定义 Lagrangian 函数:
$$
L(x, \lambda, \mu)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{j=1}^{p} \mu_{j} h_{j}(x)
$$
从下面 4 点理解 Lagrangian 函数:
- 因为带约束的优化问题 (原问题), 求解起来比较困难, 所以将原问 题中的不等式约束 $f_{i}(x)$ 、等式约束 $h_{j}(x)$ 和优化目标 $f_{0}(x)$ 以加权求 和的方式融合在一起, 将新得到的函数称为 Lagrangian 函数;
- 其中 $x$ 叫做原变量 (primal variables)。相对于原问题, Lagrangian 函数引人 2 个新的变量 $\lambda, \mu$, 变量的维度分别和不等式的约束个数以 及等式的约束个数相等, 即 $\lambda \in \mathbf{R}{0+}^{m}, \mu \in \mathbf{R}^{p}$, 将 $\lambda, \mu$ 命名为 Lagrange 乘子, 也叫对偶变量 (dual variables)。需要注意不等式约束的系数 $\lambda{i}$ 非负, 即 $\lambda_{i} \geq 0$, 等式约束的系数 $\mu_{j}$ 可以是任意实数;
- 当 $x$ 固定时, $f_{0}(x), f_{i}(x), h_{j}(x)$ 均为常数, 此时 Lagrangian 函数 是关于 $\lambda, \mu$ 的线性函数;
- 在可行域 $\mathcal{D}$ 内, $f_{0}(x) \geq L(x, \lambda, \mu)$ 。因为 $h_{j}(x)=0, f_{i}(x) \leq 0$, 代 人式 $3-5$, 便得到这个结论;
4. Lagrage 对偶函数/对偶函数
有了 Lagrangian 函数,我们再引入 Lagrange 对偶函数如式3-6:
$$
g(\lambda, \mu)=\inf _{x \in \mathcal{D}} L(x, \lambda, \mu)
$$
Lagrange 对偶函数是 Lagrangian 函数关于 x 取最小值时的函数。Lagrange对偶函数有以下 2 点性质:
- 性质 1. $g(\lambda, \mu)$ 为凹函数。这里我们不严格证明,结合图像直观理解 下。我们知道对于一个固定的 $x, L(\lambda, \mu)$ 是关于的 $\lambda, \mu$ 的线性函数, 所 以 ${L(\lambda, \mu), x \in \mathcal{D}}$ 表示一族线性函数, 在一族线性函数中, 取最小 值, 会得到一个凹函数;具体如图3-1中红色实线所示。
- 性质 2. $g(\lambda, \mu)$ 是原问题最优值的一个下界。证明过程参考如下。