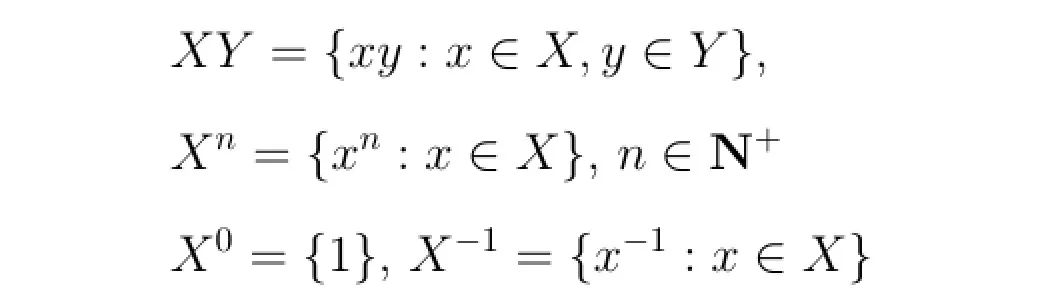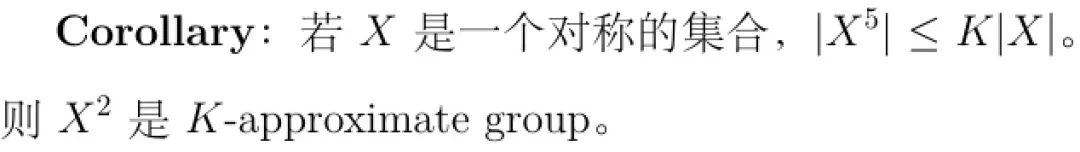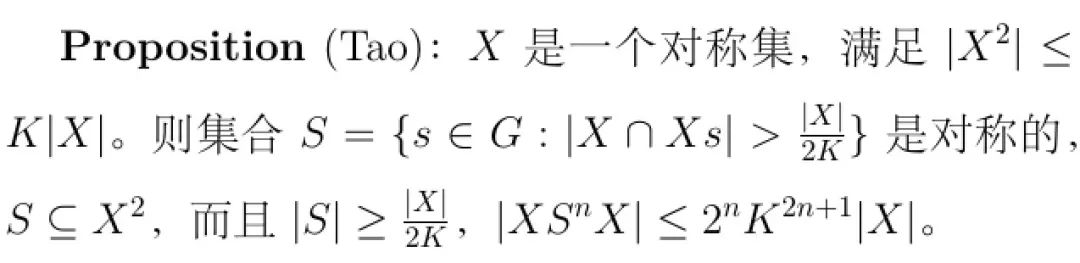一个群中的群（子群），是一个子集加上限制在其上的运算构成的，要求其内的运算封闭。一个群中的approximate group 也是一个子集加上限制在其上的运算构成的，但相比于群，放宽了定义中对封闭性的要求。

本文将讲述荆老师在加性组合课上[1]讲述的与approximate group有关的一些性质，这些性质几乎都关于找出某个有着好性质的集合。

只需要基础的抽象代数知识即可读懂本文。欢迎大家与我讨论问题，可以发评论也可以给公众号直接发消息。

先说一下一些定义：

在本文中用G来表示一个群，单位元为1，用 · 来表示G中的运算。本文中所有的运算都是在一个群G内的，故我们直接说“一个集合X”来表示“G的一个子集X”；说到集合X、Y、S时，默认它们都是有限的；当出现分数 个 时，默认是指这个分数的下取整 个；当说一个集合比较大时，默认是指它的size 比较大。

对两集合X与Y，定义集合的运算：

X的一个left coset 是一个translation gX。

称X是对称的，如果X=X^-1且G的单位元1**∈X。

|X^3|/|X|为X的tripling number， |X^2|/|X|为X的doubling number。

一、Approximate group 的定义与一些明显的性质

由定义可见，1-approximate group 满足X^2=X，是一个group。

举一个例子：在整数群中，X={-N,-N+1,…N-1,N}是一个2-approximate group。

如果X是一个对称集，且X^2被X的数个left cosets覆盖，有一个很明显的性质（可以直接在左右两边乘X来证明）表明X的高次方被X覆盖：

二、Ruzsa’s covering lemma 与两个corollary

当G是非交换群时，|XY|与|YX|可以有很大的不同（甚至当Y=X^-1时）。Ruzsa’s covering lemma 告诉我们，如果|XY|相比于|Y|“不那么大”，那么X可被“不那么大”个YY^-1(一个对称集)的左陪集覆盖。

Ruzsa’s covering lemma 有两个有意思的corollary：

​ 第一个corollary给了X的一个类似于核的对称集S：

为便于理解，不妨设S在X中。它告诉我们，如果S^4在X^4中，且S在X中不太小。那么S^4在X^4中也不太小（因为X^4可被K^7/c个S^2的left cosets 覆盖），即S的膨胀（从一次方到四次方）速度和X差不多。

​ X^2比较小(|X^2|≤K|X|)时，不能得出X是K-approximate group。一个很自然的问题是找到最小的n，使当X^n比较小时 X是K-approximate group。

第二个corollary 便关于此问题，它说明当X是对称集且|X^5|/|X|比较小时，X^2是K-approximate group：

对X^4和X用Ruzsa’s covering lemma 即可得到证明。

后面的引理可以对这一corollary进行改进，把五次方缩到三次方。

三、Ruzsa’s distance 与 small tripling

​ Ruzsa’s distance 是对两个集合X与Y之间的很重要的定义。

关于问题“找到最小的n，使当|X^n|≤K|X|时 X是K^O(1)-approximate group”，我们可以用Ruzsa’s distance给出如下引理，引理的前半部分（“而且”之前）说明若X对称，那么我们只需要考虑n≤3时即可：

​ 此引理的后半部分是第二个推论的改进，即如果X有着small tripling（|X^3|/|X|小)，则X^2是K^O(1)-approximate group。

接下来的例子说明small doubling不能推出small tripling：

三、Tao’s proposition 与它的一个**应用**

Tao’s proposition说明，对一个small doubling的对称集X，可以得到一个对称集S，S的性质非常好，S在X^2中，S不小而且XS^n X不大：

S有着好的性质的原因是：可以想象有着small doubing的对称集X内部有一个群，S比较贴近这一个群。

证明需要新的工具，用局部紧群上的haar测度来拓展集合的大小。我将在下一个笔记中阐述这种方法并给予证明。

​ 通过Tao’s proposition，我们可以得到一个关于small doubling的定理：

这个定理是说，虽然small doubling不能推出X是K-approximate group。但我们可以找一个新集合Y，Y是K^O(1)-approximate group，而且可以把X有限次覆盖。

四、Helfgott slicing lemma 与 Sanders-Croot-Sisask theorem

​ Helfgott slicing lemma 表明，对一个K-approximate group X和任意子群H，Y= X^2交H 具有很好的性质：

​ 由于X^2与X的差别不太大，所以我们说Y essentially 包含在X中，而Y有着很好的性质，从而有些证明中可以利用此引理来进行归纳。

​ 最后我们说一下Sanders-Croot-Sisask theorem。这个定理是说，small doubling可以看作一种凸性，所以可以对X收缩出一个很小的核S，使S的高次幂essentially 包含在X中。

​ 在证明此定理之前，先给出一个可以用数学分析和反证法证明的引理，在这里省略掉具体证明：

​ 在Sanders-Croot-Sisask theorem 的证明中，涉及到一个很重要的集合S，S在很多定理的证明中都有用，所以我们把S的构造和性质单拿出来说：

利用S即可证明Sanders-Croot-Sisask theorem：

​ 接下来的证明是老师留的homework，我参考了[2]中证明定理5.3时用到的方法。

​ 关于approximate group的更多内容，可以查阅参考文献[2]。

[1] 荆一凡：”Additive Combinatorics” in SDU https://www.bilibili.com/video/BV1154y1s7Mm

[2]Emmanuel Breuillard, Beb Green, and Terence Tao :THE Structure Of Approximate Groups