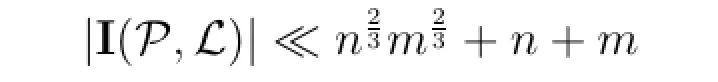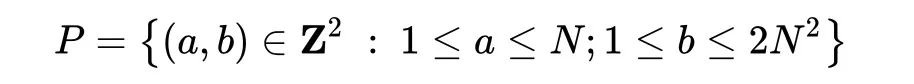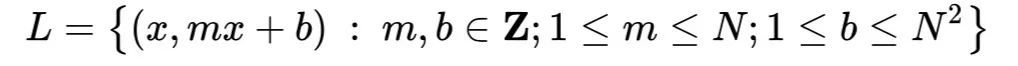​ 选取一个划分，将一个区域或集合划分为若干块，以此来对每一个块进行分析，从而得到一些结果。这种方法被称作划分法。荆老师在加性组合课上[1]，讲述的Szemeredi-Trotter 定理的证明以及此定理的两个引理，都用到了划分法。

​ 本文将通过这两个引理与Szemeredi-Trotter 定理的证明，来展示划分法的魅力。

​ 先介绍一下相交数与Szemeredi-Trotter 定理：

​ 如果在二维实数空间中有一个n个点构成的集合P，与一个m条直线构成的集合L。点与直线的所有交（一个点落在一条直线上称这个点与这条线形成一个交）组成的集合记为l(P,L)，总数记为相交数|I(P,L)|。关于相交数有一个著名的结果，Szemeredi-Trotter 定理给出了它的一个紧的[2]上界：

设N是一个正整数，对以下的点集和直线集，可以得到|I(P,L)|=N^4，说明界是紧的。

​ 接下来我们先用划分法证明有关相交数|I(P,L)|的两个引理，再介绍多项式划分法的理论依据cell decomposition，最后用多项式划分法和第一个引理给出Szemeredi-Trotter 定理的证明。

一、相交数上界相关的两个引理

​ 引理1按某种给定的规则，把直线集*L*划分为两个部分*L1*与*L2*，分别计算|I(P,L1)|与|I(P,L2)|的上界来得到相交数|I(P,L)|的一个上界：

​ 我们用f(n)~g(n)表示f(n)<<g(n)与g(n)**<<f(n)同时成立。

引理2将点集*P*划分为*k*个尽可能相同大小(*|Pi|~ n/k*)**的份*P1,…,Pk**，从而将I(P,L)分为k份I(Pi,L)，i=1,…,k。在每一份中使用上一引理，即可得到相交数|I(P,L)|*的另一个相对更好的上界：

引理2给了我们启发：如果使用更精巧的划分，可能会得到更好的估计。所以，我们引用多项式划分，使用多项式划分就可以证明出更好的界—-Szemeredi-Trotter 定理。

二、多项式划分的理论基础—Cell decomposition

​ 用Z(Q)表示一个多项式Q的零点集。

​ Cell decomposition 定理给出了一个多项式Q的存在性，这个多项式把*R^d\Z(Q)*划分为了一些开集（称作cells）的并，每个cell里所含的点都差不太多：

​ 用Cell decomposition 定理即可得到一个多项式划分。这里列举两个特殊情况来加深理解：取d=1，R上的N个点。把R画为x轴。

​ 如果取D=1，那么就有一条直线把x轴分为两部分，每部分中包含的点数不超过N；如果D=N，由拉格朗日插值可知有一个N次多项式以这N个点为零点，这个多项式把x轴分为N+1个cells，每个cell包含0个点。

​ Cell decomposition 定理的证明需要几个与点集划分相关的定理，由于本文的主题是展示划分法的魅力，故不详细证明此定理。详细的证明可以看荆老师的课（第二节课的第92分钟–第三节课的第13分钟）。

​ 我们在这里只简述一下下：

​ 先利用超球面S^m到R^m上连续映射F的一个定理，通过构造一个映射来证明Polynomial Ham Sandwich 定理：给定一些开集，存在一个多项式均匀穿过每一个开集，把每个开集分成一边正一边负（Q的取值）。

​ 接下来再用Polynomial Ham Sandwich 定理，通过取邻域，再利用球面的紧性（无限列有收敛子列），来得到一个推论：任给N个点集S1,…,SN，存在一个多项式将每一个点集Si中的点的数量大致地对半分。

​ 最后，用数学归纳法，将数学归纳法得到的多项式与推论得到的多项式相乘，就可以得到Cell decomposition 定理：任给N个点，存在一个多项式把这些点大致地平均分。

三、Szemeredi-Trotter 定理的证明

为了用多项式划分法证明Szemeredi-Trotter 定理，我们需要对R^2中的点集P用Cell decomposition 定理，得到一个多项式划分。

​ 根据Z(Q)，把|I(P,L)|像前两个引理那样分为三部分。对其中的两个部分，通过计算每一个cell中这个部分的样子、引理1、多项式的零点的性质，就可以得到这两部分各有的上界；由于划分可以使直线集L变小，通过数学归纳法可以得到另一部分的上界。把这三个部分的上界相加就可得出Szemeredi-Trotter 定理中的界：

​ 可以看出，相比于引理2的划分，我们所采用的多项式划分法可以充分利用多项式的性质，从而得到了更好的界。

​ 多项式划分法利用了多项式的性质，对多项式划分法的深入了解可以看参考文献[3]。除了多项式划分法，或许会有更精巧的划分，感兴趣的同学可以自己翻阅资料。

参考文献：

[1] 荆一凡：”Additive Combinatorics” in SDU https://www.bilibili.com/video/BV1154y1s7Mm

[2] Wikipedia: Szemerédi–Trotter theorem https://en.m.wikipedia.org/wiki/Szemer%C3%A9di%E2%80%93Trotter_theorem

[3]Eric Naslund: Yufei Zhao’s Polynomial Methods in Combinatorics