3.异形骰子

题目：

• 同时掷10枚骰子，计算所有骰子点数之和被7整除的概率。

• 考虑一种有F个面的骰子，假设投掷一次可以等概率的得到点数1,…,F。同时投掷m枚这样的骰子，

​ 计算所有骰子点数之和被N除余k的概率。

答案：

1. `python
   import numpy as np
   dp = np.zeros((11, 61))
   for i in range(1, 7):

   dp[1, i] = 1 / 6
   

   for i in range(2, 11):

   for j in range(i, 6 * i + 1):
       dp[i, j] = dp[i - 1, max(j - 6, 0) : j].sum() / 6
   

   print(dp[10, ::7].sum() * 7)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

   ​ 利用动态规划可以得到结果为14.2857%，其中dp[i, j]代表的是i个骰子掷出j点的概率。 2. 同样采用动态规划，只需要将上述代码中固定的参数改成变化传入即可，这里采用第一问作为默认参数输入 ```python def solve(F, m, N, k): dp = np.zeros((m + 1, F * m + 1)) for i in range(1, F + 1): dp[1, i] = 1 / F for i in range(2, m + 1): for j in range(i, F * i + 1): dp[i, j] = dp[i - 1, max(j - F, 0) : j].sum() / F return dp[m, k::N].sum() print(solve(6, 10, 7, 0))

4.刺杀骑士团长

题目：

枪手和骑士团长共处在一个正方形的房间，两人的位置固定不动。枪手的目标是射杀骑士团长，假设子弹可以在四个墙面上完全弹性反射，没有能量耗散。骑士团长可以在房间布置有限个护卫以格挡特定方向的子弹，请问：

• 有没有一种办法选择这些护卫的位置，使得无论枪手沿任何方向射击，都无法击杀骑士团长？

• 当房间是三维的正方体，六个墙面都可以完全反射子弹。有没有一种办法选择这些护卫的位置，使得无论枪手沿任何方向射击，都无法击杀骑士团长？

答案：

由于在平面/空间展开后，会出现多次对称的情况，也就是在(K1+x, K2+y)对应到(0,0)和(1,1)围成的正方形可能是(x,y)或者(x,1-y)或(1-x,y)或(1-x,1-y)，三维空间同理。

第一小问：可以

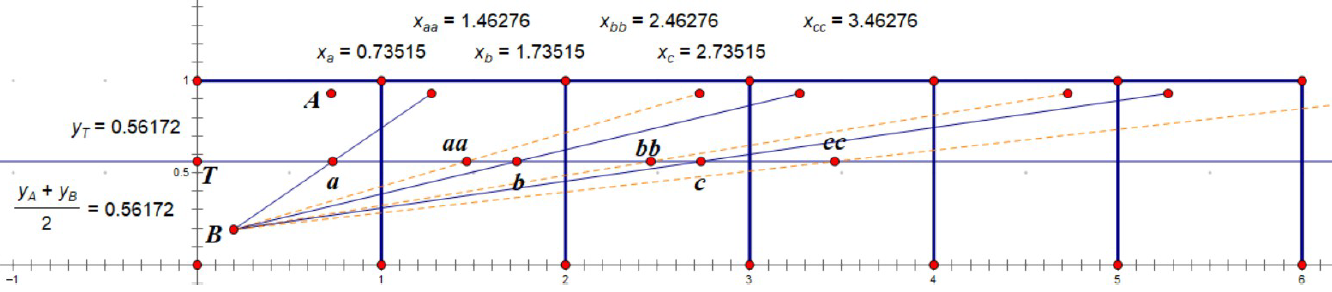
如图，在(0,0)和(1,1)围成的正方形，考虑到对称性，向四面发射子弹是等价的，这里只考虑一面，A在B的右上方。AB随机放置分别为枪手和团长，右边的红点是A的一种镜像对称。

1)不反射，则连线上随意阻挡一个位置即可

2)若只在两面上反弹

奇数即上图蓝色细线，可以看到在各种射击路线上在以AB纵向中线的位置上总会经过有规律的横坐标，即对1余数相同，这点可以通过很简单的代数计算证明，不再赘述。考虑到对称，在这里只需在(0.73515,0.56172)和(0.26485,0.56172)即可阻挡，即(1/2±(Ax-Bx-1)/2, (Ay+By)/2)；若反射偶数次为橙

色虚线同理，在(0.46276,056172)和(0.53724,056172)即可在(1/2±(Ax+Bx-1)/2, (Ay+By)/2)处阻挡。向其他方向射击同理。

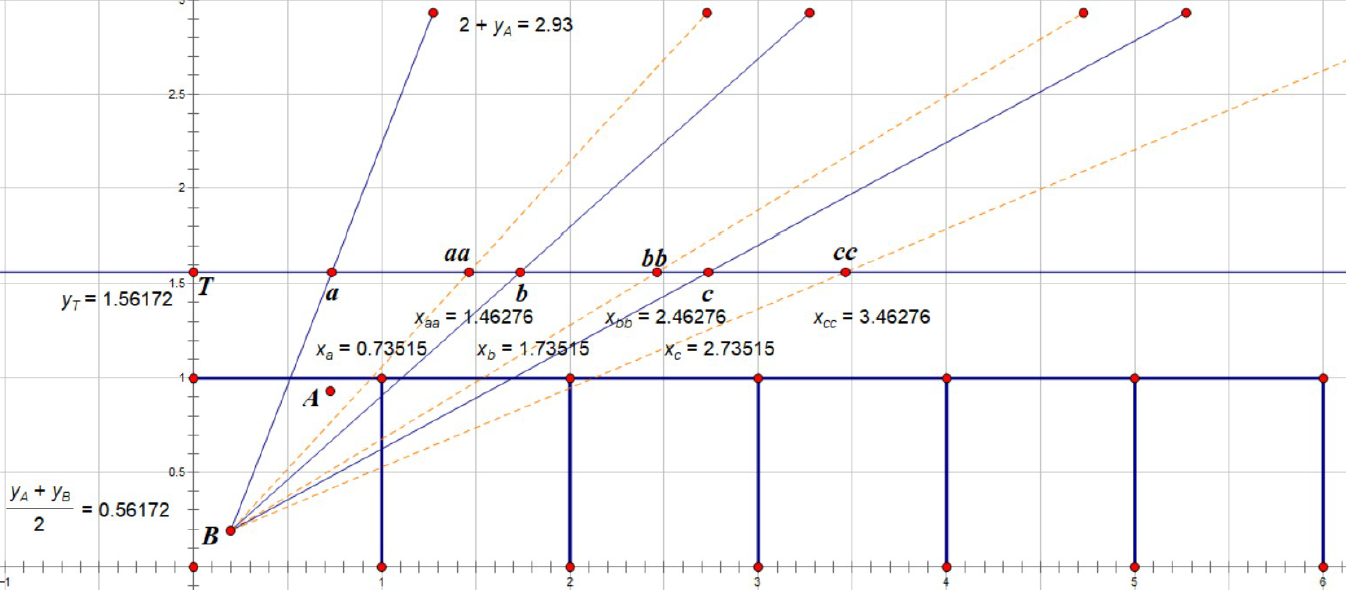
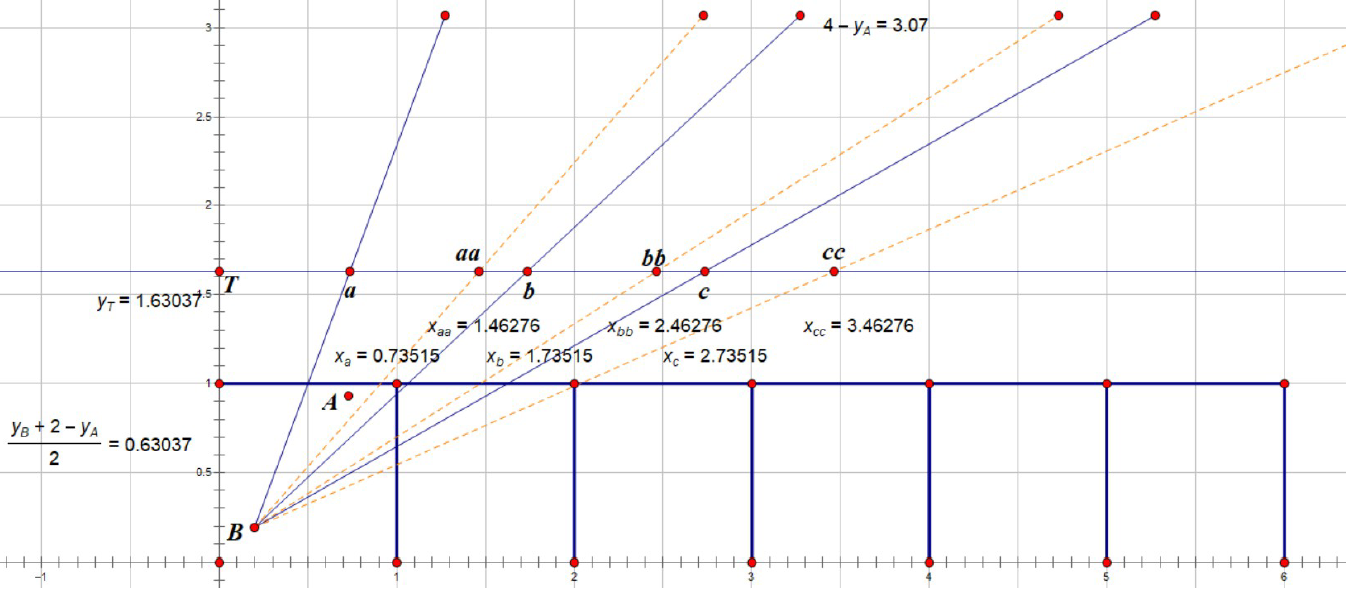
3)在更多的面上反弹

类似于2)，这里需要对在上下面反射次数的奇偶性分别讨论。在上下面反射偶数次时中心点的纵轴坐标尾数均为0.56172，即(Ay’+By)/2%1=(2k+Ay+By)/2%1=(Ay+By)/2，但这里也有对称情况，需在两个纵坐标上阻挡，横坐标和2)计算方式相同，为(1/2±(Ax-Bx-1)/2, 1/2±(Ay+By-1)/2)，(1/2±(Ax+Bx-1)/2,

1/2±(Ay+By-1)/2)

反射奇数次如上图纵轴坐标尾数为(Ay’+By)/2%1=(2k-Ay+By)/2%1=(2-Ay+By)/2，考虑到对称情况，需在两个纵坐标上阻挡，故挡的位置为(1/2±(Ax-Bx-1)/2, 1/2±(Ay-By-1)/2)，(1/2±(Ax+Bx-1)/2, 1/2±(Ay-By-1)/2)

综上所述，可以用有限的士兵阻挡住所有子弹

第二小问：可以

设立方体边长为1，在第一象限，枪手团长位置分别(Ax,Ay,Az)和(Bx,By,Bz)，则B经过若干次反射可以表示为(2Kx±Bx,2Ky±By,2Kz±Bz)，Kx,Ky,Kz均为整数。A,B连线的中点为(2Kx+Ax±Bx,2Ky+Ay±By,2Kz+Az±Bz)/2，不考虑反射时导致相对坐标发生对称变换，则对应在该立方体内坐标为(Ax±Bx,Ay±By,Az±Bz)/2，即必将经过这几个点；考虑到反射导致的对称，对该坐标分别对x=1/2,y=1/2,z=1/2平面多次对称变换，即可覆盖所有的中心点。也可将子弹在立方体内运动分解为前后、左右、上下三个方向分量，枪手团长的位置也是同理。每个分量上均可用有限个士兵阻挡，则对于每个阻挡的坐标分别在三个方向上做变换，可阻挡所有子弹。

故用有限的士兵可以阻挡住所有子弹

5.必胜策略

题目：

Bob和Alice被邀请参加一个卡牌游戏。庄家从一组扑克牌(四种花色，A-K)给Bob随机发放5张。Bob可以选择其中四张依次展示给Alice看，然后Alice被要求猜测Bob手中剩下的一张牌的花色和点数。

问：Bob和Alice能否仅仅根据牌的花色和点数设计出一个策略，使得无论Bob拿到的是哪五张牌，Alice都能成功猜测出最后一张牌的花色和点数。

答案：

​ 确定一张牌需要花色加上点数

​ 首先是花色，花色由于抽屉原理，一定会有两张相同花色的牌。那么可以将一张牌当作被猜的牌，另一张被第一个翻出，当作花色指示牌。

​ 目前，花色已经被确定了。

​ 对于点数而言，剩下的三张牌可以考虑预先对于花色和点数的组合大小进行一个定义，那么三张不同的牌一共涉及种排列方式，而13张牌A-K排成一个圆周，每一张牌到剩下十二张牌的距离都在6以内（顺时针或逆时针），而13张牌A-K排成一个圆周，每一张牌到剩下十二张牌的距离都在6以内（顺时针或你是这）。于是可以预先定义顺/逆时针，然后以第一张标示牌沿顺/逆时针走k格。k为之后三张牌组合出来对应的数字，由于bob拥有一定的自主选择权，可以通过对调第一张牌和最后一张牌的方式来确定一定可达。

​ 这里对题目给出的例子进行分析：

​ 首先预先约定定义方向为顺时针，花色大小约定为♠️>♥️>♣️>♦️

​ 那么我三张牌中假设最小的一张牌为牌A，次小为牌B，最大为牌C。一共有六种组合对应六个数字：

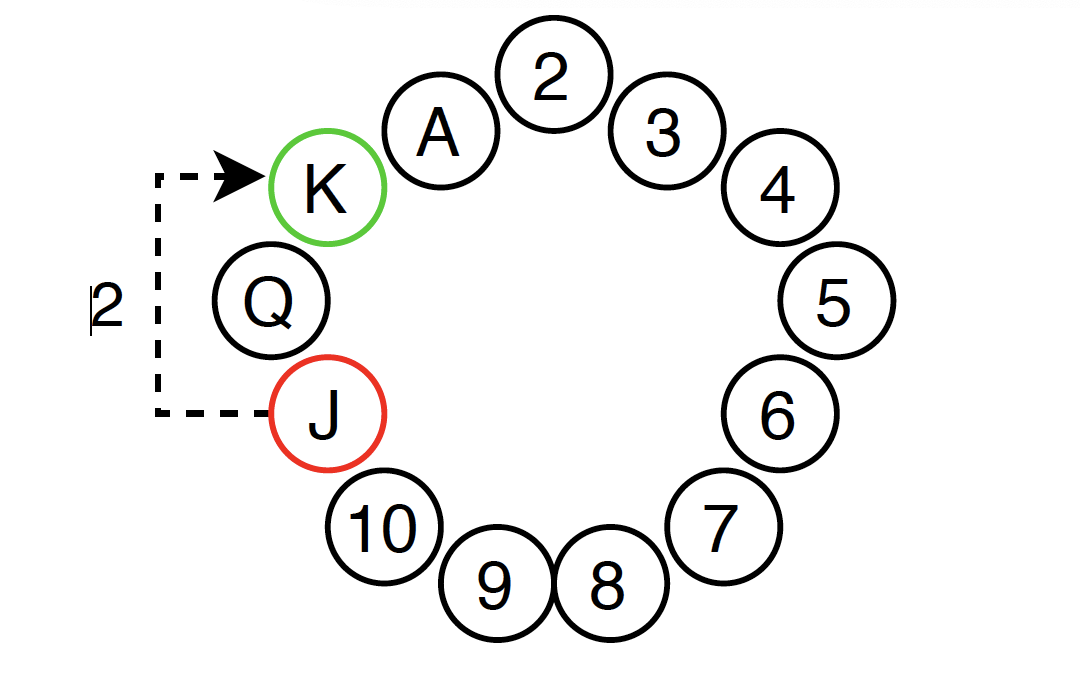
​ 现在Bob亮出♦️J，并且打算让Alice猜♦️K，已经确定了花色为♦️。

​ 之后顺时针需要走两格，所以需要组合出数字2。

​ 按大小区分剩下三张牌可以认为♥️2为牌A，♠️3为牌B，♠️9为牌C，那么对应于数字2的顺序为ACB。

​ 所以最终得到的亮牌顺序为♦️J，♥️2，♠️9，♠️3，Alice可以猜出最后一张牌为♦️K。

智力测试题

问题1：

​ 白鹭的小伙伴们酷爱乒乓球双打。男生们的水平尤为出色。当两男生对战一男一女时，有女生的一边每得一分的概率只有,现在两方约定，有女生的一方只要得五分就算赢下这一局，两男生的一边则要得11分才算赢下这一局

​ a.请问有女生的一边赢得一局的概率是多少？

​ b.若保留赛点制，即当双方比分打到10:4时，需要领先对方2分才算赢得比赛。请问有女生的一边赢得一局的概率是多少？

回答1：

​ a.使用动态规划，用矩阵表示第几局，女生组赢几局，最后一局女生赢。即考虑女生赢四局，男生赢十局内的可能性之和/3，则最多打14局

1
2
3
4
5
6
7
8
9
10
11

import numpy as np

def func(p, g, b): # 女生赢概率，女生赢的局数，男生赢的局数
		cnt = np.zeros(shape=(g+b-1, g))
		cnt[0,0] = 1
		for i in range(1, g+b-1): # 第i局
				cnt[i, 0] = cnt[i-1, 0]*2/3 # 一直输
				for j in range(1, g): # 女生赢j局
						cnt[i,j] = cnt[i-1, j]*2/3 + cnt[i-1, j-1]*1/3
				return cnt[:, g-1]
print(sum(func(1/3, 5, 11))/3)

输出结果为59.59%

​ b. 首先对于平局情况，即对于任意 的比分情况下，女生队赢得比赛可能性进行 分析, 可以列出如下方程。其中:

• 表明女生领先情况下, 即 比分下, 女生赢的概率
• 表明男生领先情况下, 即 比分下, 女生赢的概率
• 表明赛点情况下, 即 比分下, 女生赢的概率

可以解得赛点情况下女生赢的概率为1/5

故女生赢的概率为0.5244995315671082+0.21430705488578325/5=0.5673609425442648

问题2：

AB两地相距20公里, 有1000升煤油需要用一台煤油车从A地运到B地。煤油车运载量是 200升。车子本身耗煤油为每公里1升。
a. 请问怎么操作可以让到达B地的煤油最多, 最多多少升?
b. 若AB两地相距 100 公里呢?
c. 若AB两地相距200公里呢?

回答2：

由bc两问可知，煤油车可在中途停车装/卸货
为了提升效率装满车，则中途装/卸货后应剩余200L的整数倍
即第一个装/卸货点为 , 剩余油为
同理
第二个装/卸货点:
第三个装/卸货点:
第四个装/卸货点:

a. 每次运满，最后一次不返回，即
b.即先后于 装/卸货，剩余 ，到100公里时还剩 )=372.3809523809524升
c.即先后于 装/卸货，剩余200L，到200公里时还剩升

问题4：

有一个只有12条棱围成的正方体铁架，有一只蜗牛在沿铁架爬行。铁架上还有乌龟在沿铁架爬行，并虎视眈眈地想捉到蜗牛成为美餐。蜗牛的速度是乌龟的三倍。
问：在初始位置任意的情况下，至少几只乌龟共同参与铁架上的围追堵截，才能捉到蜗牛? 并请详述捕捉方案。

回答4:

需要3只, 方案如下图所示, 两只乌龟负责掌控两条红色的对角棱边。在这个控制下蜗牛 只能在绿色部分爬行, 如图所示，两只乌龟仅在对称边上运动，由于速度3:1，则蜗牛无论怎么跑，在对称两边上的乌龟总可以在的离蜗牛近的边的1/3处，另一只追赶蜗牛。考虑对称对应背面的黑色部分, 两种情况实际上是等价的。

算法题

问题1

现有一个整数数组。

问：求所有符合要求的子序列的和的最大值，要求该子序列至少有两个值，且第一个值和最后一个值相同。

解答

遍历数组，得到与每个值相等的最大索引，并计算各位置正值总和，以获得子序列最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import numpy as np

def func(lis): # 若没有符合的子序列返回None
		index = {} # 每个值的最大索引
		lis_sum = [0] # 列表前i个数值之和(不含i，只计算正值，其他记0)
		sub_max = [] # 符合要求的子序列和
		for i,x in enumerate(lis):
				index[x] = i
				lis_sum.append(lis_sum[-1]+x if x>0 else lis_sum[-1])
		for i,x in enumerate(lis):
				if index[x] != i: # 该数字出现超过一次，可以成为子序列首尾
						sub_max.append(lis_sum[index[x]] - lis_sum[i+1] + x*2)
		return max(sub_max) if sub_max else None
		
lis = np.random.randint(-5,5,20)
print(lis)
print(func(lis))