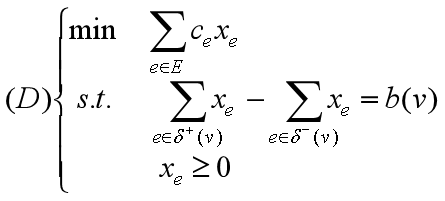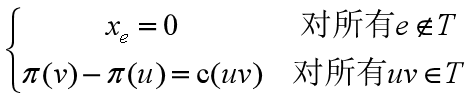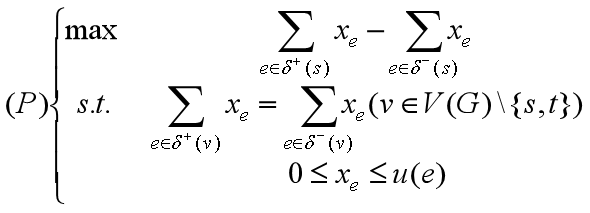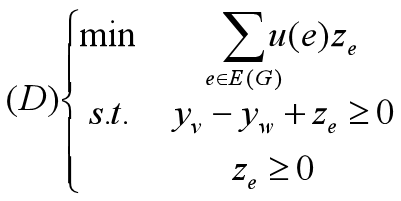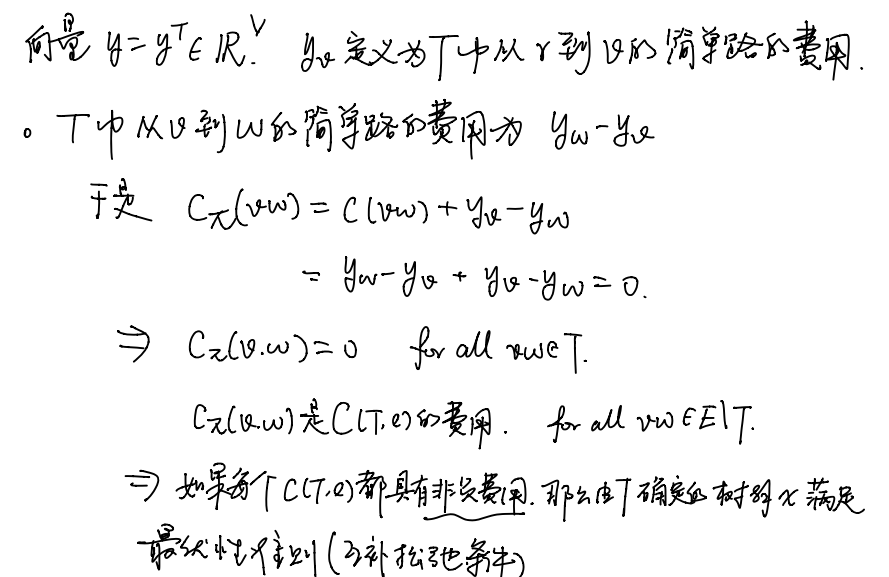在实际应用中。迄今为止求解线性规划问题著名的仍是单纯形法。通过专业的实现,它具有卓越的性能:≈1000变量和≈1000约束的问题可以在0.1到0.5秒内得到解决。那么,是否可以尝试将该算法应用于图论中的问题呢?
事实上,最重要的网络优化问题都可以用线性规划来表示,比如确定最短路、最大流、最小费用流等。然而,直接应用通常的单纯形算法是没有意义的,因为所产生的程序将是笨拙(unwiedy)和高度退化的(highly degenerate)。这两个问题通过使用单纯形法的适当图论特殊化来避免:网络单纯形法。
在此之前,我们先从最短路的故事说起。
我们知道所有解决最短路问题的方法的基础是下面这样一个简单的想法:假设已知对每个v存在一条费用为π(v)的从r到v的有向路,并且我们找到一条满足π(v) + C(vw) < π(w)的弧vw。由于把vw附加到从r到v的有向路可以得到一条到w的有向路,因此存在一条到w的费用为π(v) + C(vw)的更便宜的有向路。基于此,定义可行势(feasible potential)的概念是自然的:
Def1.如果π(v)是到v的有向路的最小费用,那么π满足π(v) + C(vw) ≥ π(w),称π是一个可行势。
可行势对最短路的费用给出了下界,我们有如下命题:
Prop1.令π是可行势且P是从s到v的有向路,那么c(P)≥π(v).
事实上,我们通过Ford算法在终止时得到了一个可行势和若干有向路,对它们来说上述命题中的等号成立。即有下面的定理陈述这个事实:
Thm1. min{c(P):P是从s到t的有向路} = max{π(t):π可行势}
我们可以通过这个陈述看到它与线性规划对偶性之间的联系。定理陈述中的最大化显然是一个线性规划问题:
对偶最优值定理告诉我们(P)(D)中有一个最优值存在,则两个最优值都存在且相等。注意到任何r到s的有向路P为(D)提供了一个可行解,则(D)的目标函数值恰好是P的费用,因此,定理1意味着,当最短路存在时,(D)有一个最优解,它是一条简单有向路的特征向量。这个结果将等价于结论:
- Prop2. (D)的可行解多面体的顶点是简单有向路的特征向量.
因为我们已经可以用Ford算法解决线性规划问题(D),那么这个算法和单纯形法之间的联系是什么呢?单纯形法保存了一个“基”弧(对应于(D)中的基变量)的集合T,(D)的一个可行解x及向量y∈R^{V},它们满足
在每次迭代中,通过用集合外的一条弧替代集合中的一条,得到一个新的这样的集合。基弧的集合T必须对应于(D)的等式约束矩阵A的列极大线性无关组(列基)。事实上,这个矩阵就是图G的关联矩阵(incidence matrix),它的列基可以用很好的方法来刻画。
Prop3.G:有向、连通,$A=\left{a_{e}: e \in E\right}$.集合$\left{a_{e}: e \in E\right}$是$A$的列基,当且仅当T是G的一颗生成树的弧集(ex.如果T不包含任何圈的弧集,那么它对应的列是线性无关的)
所以在这样的观察下,我们可以知道单纯形法是从生成树到生成树,每一步都可以看作是一序列的Ford算法步骤,她是一个被若干个不改变树的步骤所跟随着的通常步骤,直到y“追赶”为树。
最大流问题同样是一个线性规划问题,所以通过线性规划对偶可以给出最大流的一个好的刻画。那么,我们的一个自然的问题就是这种刻画与我们通过割所给出的刻画有什么联系。
同样由对偶最优定理,我们可以给出经典的最大流-最小割定理的如下刻画: 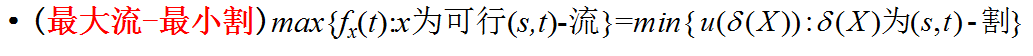
现在故事来到了最小费用流问题(MCFP),它的一个标准陈述如下: 
我们·可以自然的写出其对应的线性规划形式:
作为一个重要的特例,我们想让其中每个u(e)都是无穷的,这样的问题称为转运问题(transshipment problem)
设x是任意的b-流,即(P)的任意可行解,则由对偶最优定理,我们有如下结论:(互补松紧性条件给出了我们想要的最优性刻画)
另外,下面两个观察是重要的:
- 给定G中的一条路P。 定义P(关于c)的费用为∑(c(e) :e是P的正向弧)-∑ (c(e) :e是P的反向弧)。这样定义的原因是:假设我们在G中沿一条x-可扩路P发送ε单位的流,即xe在P的正向弧上提高了ε,在P的反向弧上降低了ε。那么cTx增加了∑(εce :e是P的正向弧)-∑ (εce :e是P的反向弧) ,即增加了ε倍的P的费用。特别的,如果x是(P)的可行解,那么某个负费用的x-可扩圈将给出一个费用更低的解。
- 对满足0≤x≤u的向量x,如同处理最大流时一样定义一个辅助有向图Gx,则G中每条x-可扩路对应于Gx中具有相同费用的一条有向路,特别的,G中一个负费用的x-可扩圈对应于Gx中一个负费用有向圈。
于是我们就可以用最短路方法来确定Gx是否包含负费用有向圈。这便引出了下面对(P)的最优性的刻画:
- Thm3.(P)的可行解x是最优的当且仅当不存在具有负费用c的x-可扩圈。
- (Klein 1967)(G,u,b,c). A b-flow f is of minimum cost iff there is no f-augmenting cycle with negative total weight iff there exists a feasible potential for (Gf , c).
这是一条最重要的最优性准则。以上基本讲清了线性规划与最小费用流问题的联系。下面在我们正式将单纯形法应用于此之前,我们首先陈述这部分内容所需要的一些基本想法:
- 假设问题定义在连通有向图G上(否则,限制在G的每个连通分支上处理即可)
- 可先对转运问题这一特殊情况进行分析(即假设对每条弧e有u(e)=∞)
- 定义转运问题的树解(支撑树解)
- 网络单纯形法保持可行的树解并且寻找一种特殊的负费用圈。(如果每个C(T,e)都具有非负费用,那么由T确定的树解x满足最优值定理的条件)
- 增加辅助边来找初始的树和流
- 避免循环:从一颗强可行树开始并使用离开弧规则(选择h是C(T,e)中第一条满足 x(h)=θ的反向弧)
- 网络单纯形法在有限步后会终止。
- 一般的,网络单纯形法将从树解移动到树解,只使用通过增加一条弧到T上形成的圈。
我们首选对转运问题来定义树解,转运问题的支撑树解(spanning tree solution)是一个向量x∈R^{E}满足条件:对某棵树T, 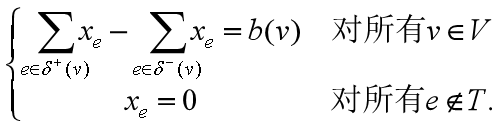
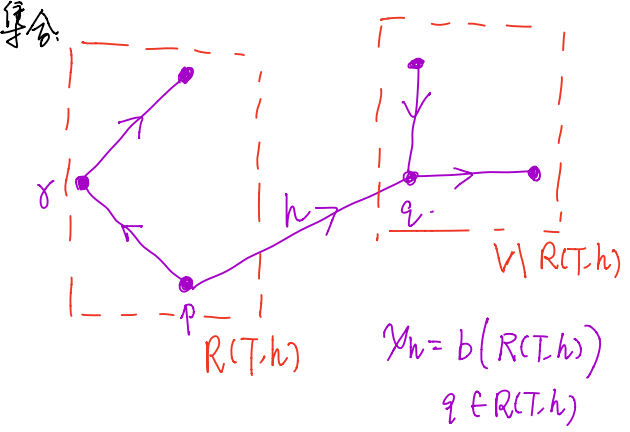
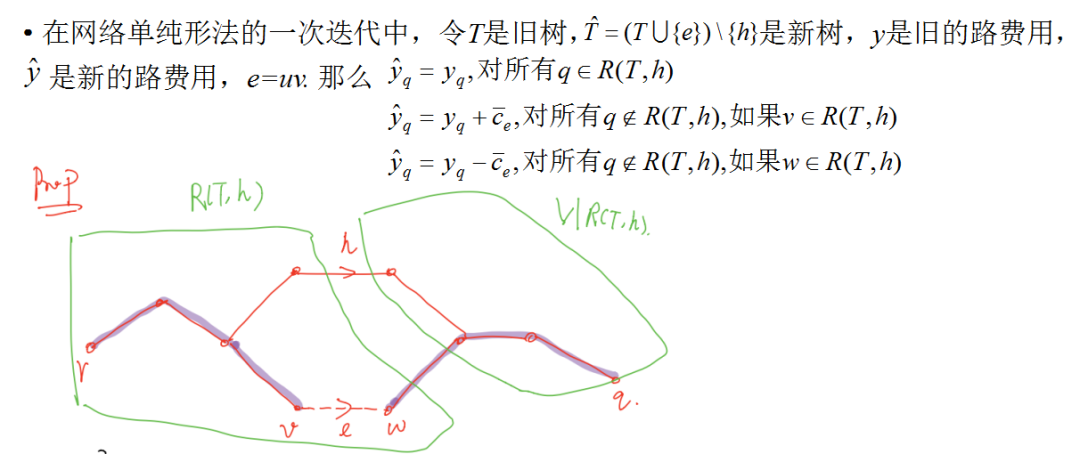
树T和T的一条弧h=pq确定了将顶点氛围两部分R(T,h)和V\R(T,h)的一个划分如下:R(T,h)是在T中从r到v的简单路没有用到h的那些顶点v的集合。显然如图,r∈R(T,h),h是T中唯一的一个端点在R(T,h)中,另一个端点不在R(T,h)中的弧。所以在与T相关的任何树解x中,流入R(T,h)的净流量一定是完全由h携带的。
这个观察将给我们下面的结果:
Prop4.一棵树T唯一地确定了它的树解.
Prop5.(G:连通) 一个可行解是树解,当且仅当不存在每条弧都具有正流的圈。
我们已经指出网络单纯形法是保持可行的树解并且寻找一种特殊的负费用圈,现在就给出这样的圈: 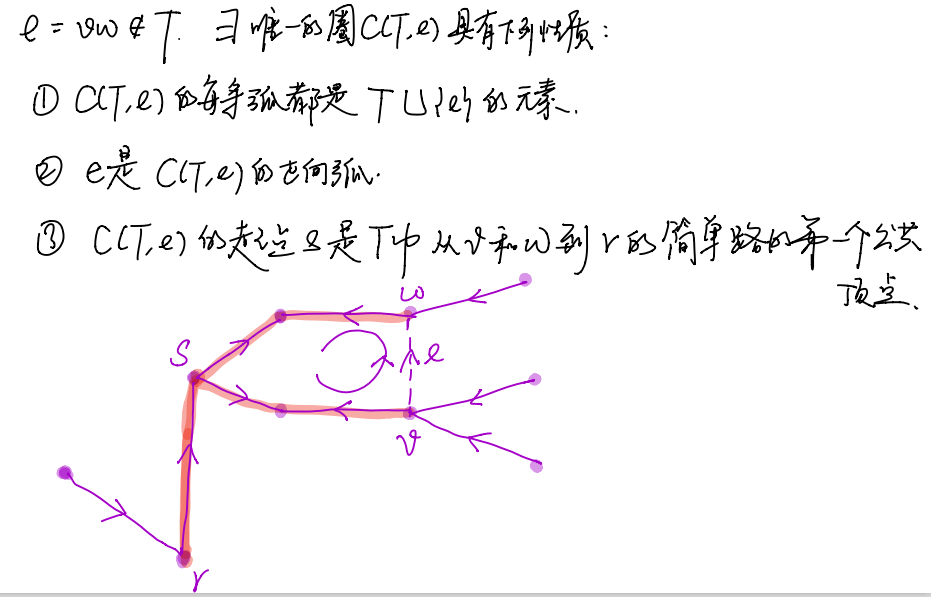
那么这种特殊类型的圈有什么优点呢?
Prop6.如果树T确定了可行树解x且对每个e不属于T,C(T,e)都具有非负费用。那么x是最优的。
有了上面的陈述,我们已经可以叙述我们心目中算法的初步形式:
这里立刻出现的一个问题是:如何找到初始的树和流。我们直接针对一般的最小费用流问题给出答案。
下面的命题演示了我们是如何从找到的圈中替换原来树上的一条弧从而实现“换基”操作的。
- Def2.如果一棵树T确定了一个满足T中至少有一条弧携带0流的流x,那么我们说x是退化的。
这直接引发了一个重要的理论问题:
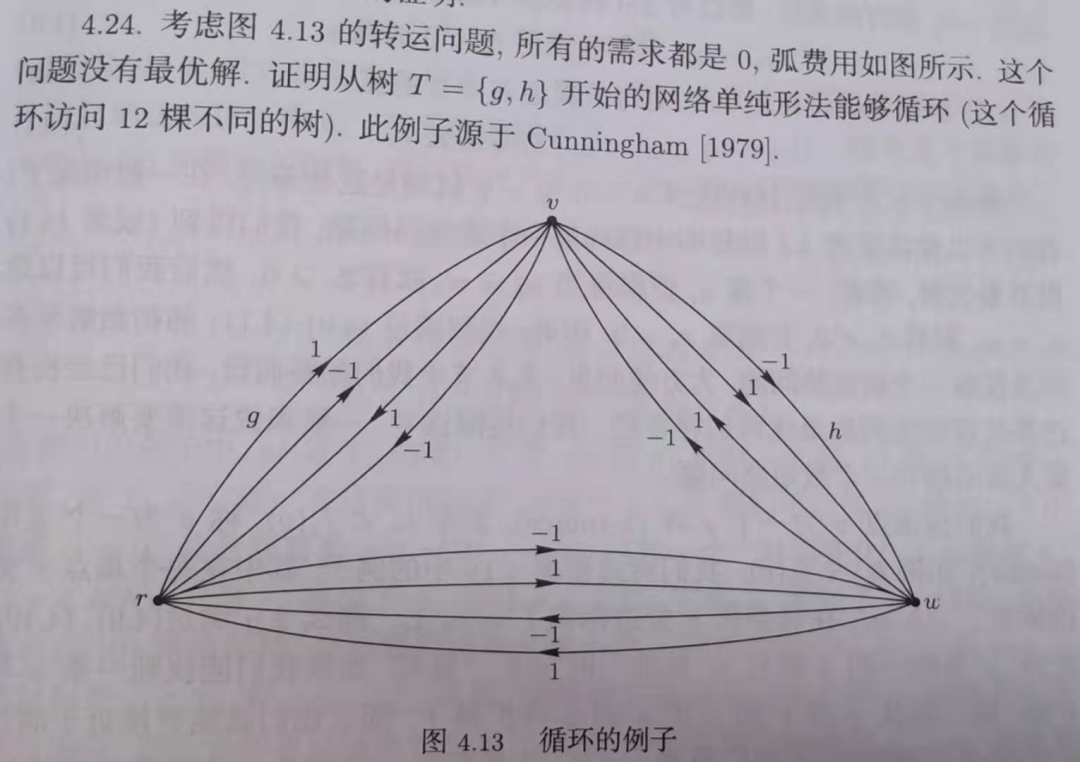
Q. 在一系列退化的迭代(改变树而不改变流的迭代只可能出现在流是退化的情况下)后,该算法会不会返回同一棵树?(循环,导致算法不能终止/另一方面,如果循环不发生,由于不同的树的数目是有限的,那么算法一定在有限步内终止。)
(注:循环是可能发生的[Cunningham],但Cook提到“尽管据我们所知,迄今为止它从未在实际问题的解决中发生)
令h=pq是T中的一条弧,我们说h在T中是远离(away from)r的,如果p∈R(T,h);否则h在T中是朝向(toward)r的。上面由一棵树和一条弧导出的划分的图中弧h是远离r的。
- Def3.一棵树T称为强可行的(strongly feasible),如果它确定了一个可行流x,使得对T的每条满足xh=0的弧h,h在T中是远离r的。
注意到如果流不是退化的,那么树平凡的满足这个条件,还注意到我们用来初始化算法的树是强可行的。现在假设我们从一棵强可行的树开始算法,并在算法的每一步,我们按如下规则选择弧h:
- 离开弧规则:选择h是C(T,e)中第一条满足x(h)=θ的反向弧。
- Thm4. 如从一棵强可行树开始并使用离开弧规则的网络单纯形法在有限步后会终止。
下面我们将转运问题的上述讨论直接扩展到解决一般的最小费用流问题的网络单纯形法,它也可以看作是对线性规划的有界变量单纯形法的一个解释。
定义树解是一个向量x∈R^{E},s.t.对某棵树T以及E\T的划分(L,U)我们有
fx(v)=b(v),对所有v∈V;
x(e)=0,对所有e∈L;
x(e)=u(e),对所有e∈U.
添加一条弧形成的圈C(T,L,U,e)满足以下性质:
C(T,L,U,e)的每条弧都是T∪{e}的元素;
如果e∈L,那么e是C(T,L,U,e)的正向弧,否则是反向弧;
C(T,L,U,e)的起点s是T中从v和w到r的简单路上的第一个公共顶点。
我们可以将之前得到的最优性定理拓展如下:
- Prop8.如果树(T,L,U)确定了可行树解x并且对每个e∉T,C(T,L,U,e)都有非负的费用,那么x是最优的。
参考文献: Bernhard Korte and Jens Vygen《Combinatorial Optimization Theory and Algorithms(6th,2018)》
Cook等《Combinatorial Optimization》