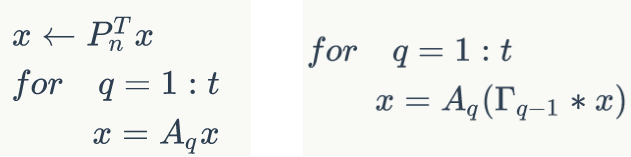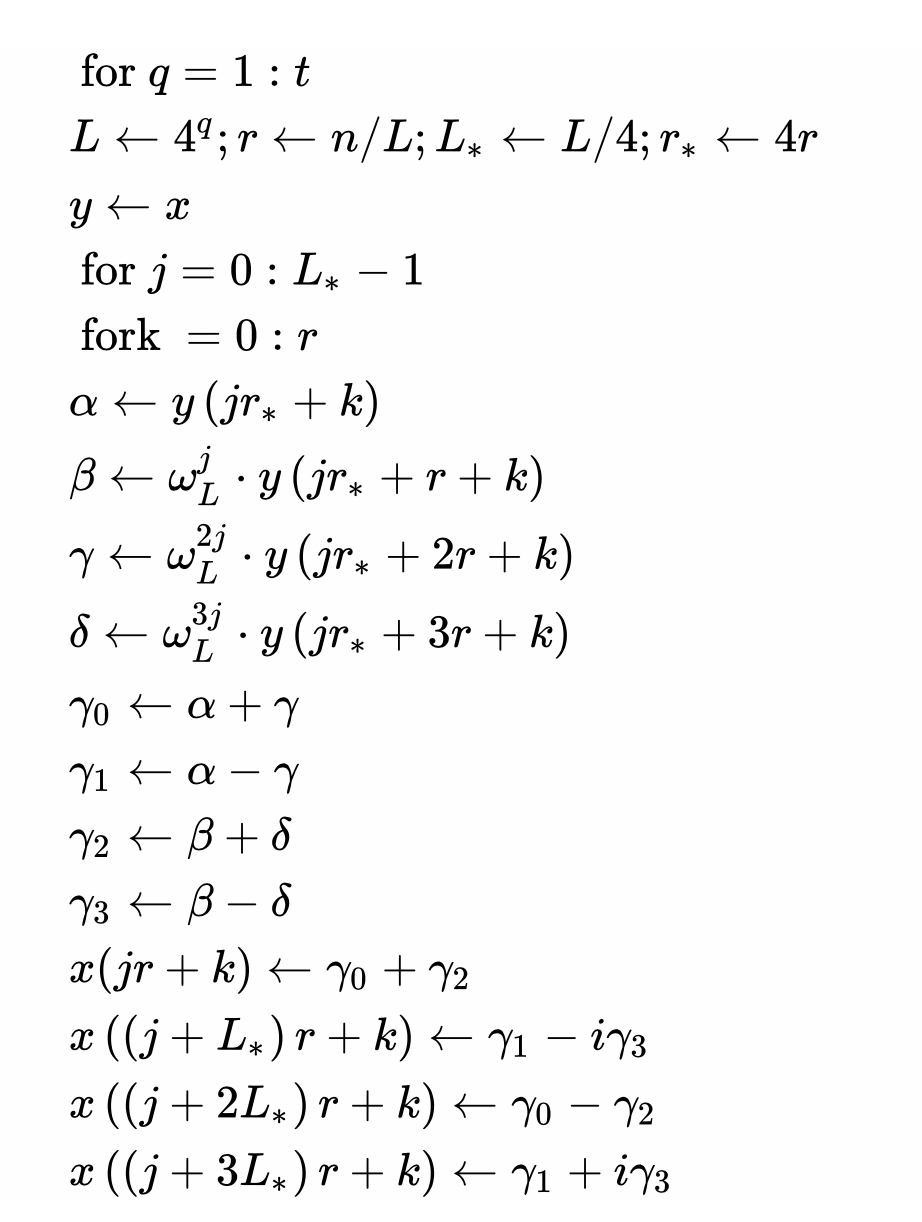一维FFT算法在Maxwell架构上,归为访存密集算法。
即,在足够优化的情况下,可在一次memory copy的耗时内完成计算。本文实现的FFT算法达到与官方库cuFFT一致的速度,通过整合kernel,可实现比调用CUFFT更快的算法整体执行速度。在处理65536*4以上大点数一维FFT+IFFT计算时(一个大核心共享内存放不下完整的一维FFT数据),组合算法可以实现比CUFFT少2个kernel调用的时间(减少两次显存数据交换),主要说明4096点FFT算法设计的思路及实现。大点数仅说明方法和测试结果。
算法原理及设计思路
本节说明快速傅里叶变换(Fast Fourier Transform)的原理和数值计算过程,重介绍能发挥GPU架构优势的算法类型。
常规FFT实现(Cooley-Tukey)
公式推导与计算结构
旋转因子W具有对称、周期、可约的特点:
$$
\begin{array}{c}
W_{N}^{k+\frac{N}{2}}=-W_{N}^{k} \
W_{N}^{2 k r}=e^{-j \frac{2 \pi}{N} 2 k r}=e^{-j \frac{2 \pi}{N / 2} k r}=W_{N / 2}^{k r} \
W_{N}^{2}=e^{-j \frac{2 \pi}{N} 2}=e^{-j \frac{2 \pi}{N / 2}}=W_{N / 2}^{1}
\end{array}
$$
Cooley和Tukey利用旋转因子的特性,将DFT进行奇偶分解:
$$
\begin{aligned}
X(k) &=D F T[x(n)]=\sum_{n=0}^{N-1} x(n) W_{N}^{n k}=\sum_{r=0}^{N / 2-1} x(2 r) W_{N}^{2 r k}+\sum_{r=0}^{N / 2-1} x(2 r+1) W_{N}^{(2 r+1) k} \
&=\sum_{r=0}^{N / 2-1} x_{1}(r) W_{N}^{2 r k}+W_{N}^{k} \sum_{r=0}^{N / 2-1} x_{2}(r) W_{N}^{2 r k}=\sum_{r=0}^{N / 2-1} x_{1}(r) W_{N / 2}^{r k}+W_{N}^{k} \sum_{r=0}^{N / 2-1} x_{2}(r) W_{N / 2}^{r k} \
&=X_{1}(k)+W_{N}^{k} X_{2}(k)
\end{aligned}
$$
式中,$X_1(k)$ 和$X_2(k)$ 分别是$X_1(r)$和$X_2(r)$的N/2点DFT。
分解之后只得到N/2点的序列,而$X(k)$有N点,还要计算另一半项数的结果,利用旋转因子的周期性:
$$
X_{1}\left(\frac{N}{2}+k\right)=\sum_{r=0}^{N / 2-1} x_{1}(r) W_{N / 2}^{r(N / 2+k)}=\sum_{r=0}^{N / 2-1} x_{1}(r) W_{N / 2}^{r k}=X_{1}(k)
$$
前半部分:
$$
X(k)=X_{1}(k)+W_{N}^{k} X_{2}(k) \quad, \quad k=0,1, \ldots, \frac{N}{2}-1
$$
后半部分:
$$
X\left(\frac{N}{2}+k\right)=X_{1}\left(\frac{N}{2}+k\right)+W_{N}^{(k+N / 2)} X_{2}\left(\frac{N}{2}+k\right)=X_{1}(k)-W_{N}^{k} X_{2}(k) \quad, \quad k=0,1, \ldots, \frac{N}{2}-1
$$
因此,只要求出(0,N/2)区间内所有$X_1(k)$ 和$X_2(k)$ 值,即可求出(0,N-1)区间内所有$X(k)$值,计算量“减半”。
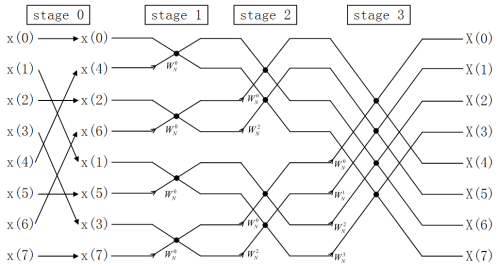
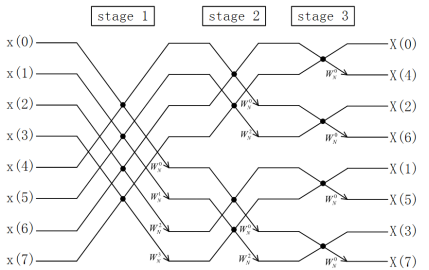
FFT算法有很多结构,但通常可归为两类,时域抽取法FFT(Decimation-In-Time FFT,简称DIT-FFT)和频域抽取法FFT(Decimation-In-Frequency FFT,简称DIF-FFT)。Cooley-Tukey方法的8点基2 FFT计算流程图如下:
从图1和图2可以清晰地看出Cooley-Tukey方法的特点:
- 从输入输出来看,DIT-FFT需要先把顺序数据倒序(Bit-reverse),再进行计算,可以得到顺序的计算结果。DIF-FFT直接用顺序数据计算,但是得到的结果是倒序的,如果需要顺序结果,还要进行处理。
- 从计算结构来看,DIT-FFT和DIF-FFT具有相反的计算结构,DIT-FFT的计算跨度(stride)是2L ,即1,2,4…2L-1 ,DIF-FFT的计算跨度相反。
- 从计算过程来看,Cooley-Tukey方法具有原址(In-place)计算的特点,一个蝶形单元的计算结果还是放到原来的位置,不需要分配暂存空间。
DFT与基-2 Cooley-Tukey DIT-FFT的程序如下:
1 | void DFTImag(Complex *Input, Complex *Output, int Amount) |
1 | void CTFFT_R2(Complex *array, Complex *array_out, unsigned int Power) |
本机CPU端计算4096点结果:
DFT的时间在2000ms左右,而FFT是4ms (Debug模式)。
DFT的时间在800ms左右,而FFT在1ms以内 (Release模式)。
考虑到GPU的硬件架构,并行化Cooley-Tukey FFT算法存在以下问题:
倒序计算
数据倒序是对序列进行奇偶抽取的结果,倒序(bit reverse)是按位进行的,把数据的MSB和LSB反向,一个简单例子是0010 0000 => 0000 0100。下面分别是8bit倒序的较快算法,本文实现的根据数据位宽倒序的算法和CUDA MATH API中的32bit数据倒序程序调用。
1 | unsigned char reverse_8bit(unsigned char x) |
1 | unsigned int |
可以看出,通常情况下要对数据进行几十次操作才能得出倒序结果。测试中使用了CUDA的库函数进行倒序,并没有比reverse_8bit快。另一个问题是,FFT kernel占用较多硬件资源,一个大核心只能保证2到3个block占用。
大量倒序计算在一些情况下会使访存密度降低(这里的意思是,在做到足够优化的情况下,算法是访存密集的,如果计算量再增加,就是计算密集的了,相同数据量的算法执行时间会增加),测试结果如下,左边表格是全带宽占用结果,红色箭头处带宽占用不满:

图3. 倒序与否kernel带宽占用测试对比
本文想到的解决办法是,使用查找表,通过纹理缓冲从显存中读取倒序索引(不占用共享内存),24KB的L1 cache基本满足小点数查找表需求,大点数会由于片上存不下,需要多次访问显存。
但倒序的计算还不是影响算法速度的关键因素。
倒序存储
《Maxwell硬件架构与编程方法》中详细说明了GPU存储结构和使用注意事项,从算法局部性考虑,FFT算法的输入数据需要从显存顺序读到片上,在共享内存中进行倒序。而共享内存分为32个32bit的存储体(bank),在这一级倒序读取或存储都会导致存储体冲突(bank conflict)。根据倒序特点和单精度浮点的复数数据结构(两个float),实际地共享内存带宽占用仅有1/16。实测结果与理论分析一致:
注意,图4和图5中的数据量不同,表格第二列是传输数据量,在无冲突访存时,加载数据量=存储数据量=实际数据量。在有冲突时,数据需要排队,而每次传输数据都是3232bit,所以浪费了很多带宽。图9中,加载数据量=实际数据量,倒序存储量=16实际数据量,即有效带宽占用仅为全带宽的1/16。
本文还做了一个无冲突共享内存访问基准测试。Maxwell架构下,数据从显存读入片上,在保证完整占用显存带宽的情况下,可以在片上进行12次无冲突的数据交换,即24次存储或读取。而一次数据倒序存储就使用了16/24的时间,那么留给计算的时间就远远不够了。
所以,要高效地利用GPU计算和存储资源,就应尽量避免倒序。
非向量化的数据抽取方式
使用CUDA并行编程,数据是按1个warp,32个线程为基本单位读取的,再加上GPU存储器特点,并行化的算法数据存取结构尽可能实现连续无间隔地访存。先不考虑倒序,以32点DIT-FFT为例:
因为是浮点复数,占用64bit,相当于有16个64bit的bank。假设用16个线程来计算,那么第一级数据的第一次读取是0-15号线程读取数据0 , 2 , … , 30。其中0,2,4,6,8,10,12,14与16,18,20,22,24,26,28,30存在bank conflict,第二次读取同理。即第一次读取有一半的bank存在冲突,共享内存带宽利用率只有一半,第一次存储同理。第二级数据可以也类似,访问索引0,4,8,12,1,5,9,13的数据被合并到一起访问,与16,20,24,28,17,21,25,29冲突……直到最后一级(32点基-2运算共5级,图中值标了前4级,最后一级类似图4的stage3)才能分别连续访问0-15与16-31,利用完整带宽。前4级的数据交换共8次,实际消耗了16次无冲突数据交换的时间,浪费了1/2的带宽。
采用基-4结构的话,只有前两级有存储冲突,但每级带宽利用率是1/4,与基-2是等效的。基-8,基-16的计算结构同理,好处是后续计算级数更少。
理论和基准测试结果表明,采用传统的FFT计算结构不利于在GPU架构上高效地进行计算。
向量化的DFT分解方法(Stockham Autosort Framework)
计算分解与结构
离散傅里叶变换可以非常多形式的分解,Cooley-Tukey FFT很好的减少了算法的空间占用(原址计算),但也存在数据倒序的问题。本小节说明Stockham结构的FFT实现,Stockham 方法以空间占用为代价避免了Cooley-Tukey过程的倒序计算。它的自动倒序结构背后的思想是把数据倒序和蝶形计算结合起来。
上一小节提到过DFT的矩阵形式, 可以简记为 $F(N)=W^{k n} f(k)$ 和 $f(k)=\frac{1}{N} W^{-k n} F(N)$ 。从矩阵分解的角度看, Cooley-Tukey FFT做了以下处理:倒序步骤用矩阵表示是一个置换矩阵 $P_{n}^{T} ;$ 包含旋转因子大矩阵 $W^{k n}$ 被分解为许多级
Tukey FFT可用矩阵表示为 $X(N)=F_{n} x(k)=A_{t} \cdots A_{1} P_{n}^{T} x(k)$ 。即数据经倒序和t级基-2运算,最终得到与原始 DFT计算方法相同的傅里叶变换结果。
用同样的方式说明Stockham的方法。与Cooley-Tukey显式的置换 $F_{n}=A_{t} \cdots A_{1} P_{n}^{T}$ 不同,Stockham通过置换矩陈 $\Gamma_{0} \cdots \Gamma_{t-1}$ 使得 $F_{n}=A_{t} \Gamma_{t-1} \cdots A_{2} \Gamma_{1} A_{1} \Gamma_{0}$, 即 $X(N)=F_{n} x(k)=A_{t} \Gamma_{t-1} \cdots A_{2} \Gamma_{1} A_{1} \Gamma_{0} x(k)$
对比两者的计算过程:
Cooley-Tukey 方法首先把输入序列x完整地倒序,再进行各级蝶形计算。Stockham 方法把倒序结构和蝶形计算结合起来,在进行蝶形计算之前将序列x进行部分倒序,经过多级倒序和计算之后,得到与和Cooley-Tukey 方法相同的计算结果。
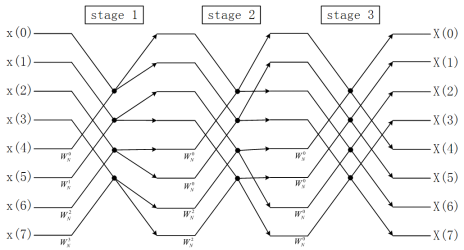
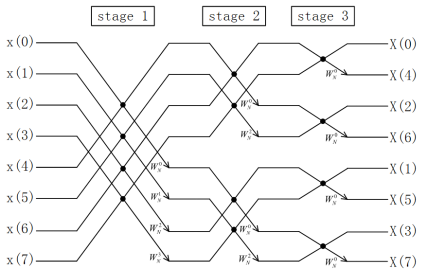
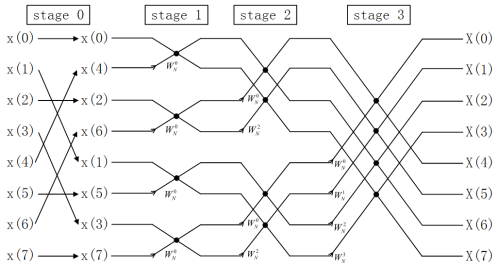
图7. 8点基-2 Stockham FFT计算流程图(DIT)
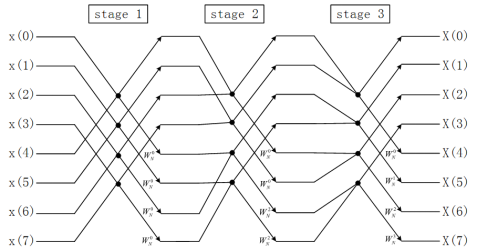
图8. 8点基-2 Stockham FFT计算流程图(DIF)
图7和图8画出了DIT 和DIF两种Stockham FFT的计算流程,可以总结出以下特点:
- 输入输出都是顺序的,没有显式的倒序步骤。
- (级间有倒序处理)计算是非原址的(Out-place),蝶形单元的计算结果可能会覆盖还没计算的数据,这就要求分配和序列长度相等的空间用来存储。
- Stockham DIT-FFT的数据读取索引是不变的,蝶形单元的数据存储跨度(stride)根据所在级数(stage)由1,2,一直到2L-1;DIF-FFT的数据存储索引是不变的,蝶形单元的数据读取跨度(stride)根据所在级数(stage)由1,2,一直到2L-1。这里,DIF的计算结构基本上与DIT相反,但计算结果一致。
算法实现与数据抽取
把《Computational Frameworks for the Fast Fourier Transform》书中1.7节的Stockham 基-2算法(书P57,PDF的第75页)用C语言实现如下:
1 | void stockham_fft_R2(Complex* x, Complex* y, int len, int power) |
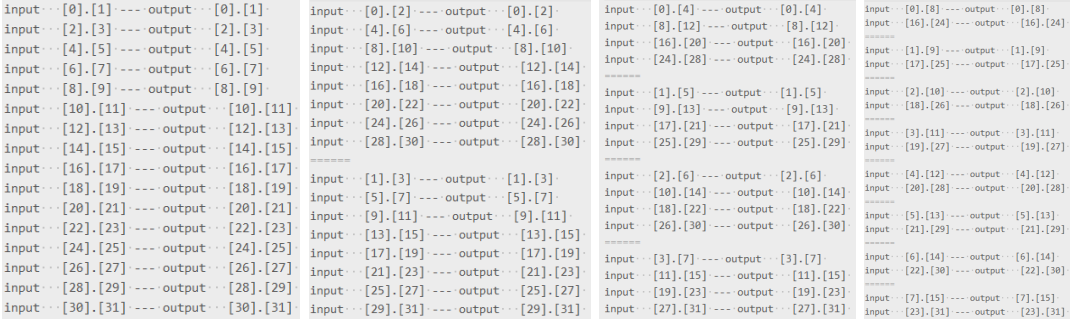
以32点Stockham 基-2 DIT-FFT计算过程的数据抽取为例。由图9可知:前4级都可实现向量化数据读取,向量化长度分别为16、8、4、2,最后一级跨度为2,不是连续的访问;所有级的数据存储都是长度为16的向量化访问。数据读取的向量化长度是和计算点数有关的,比如256点的计算,向量化长度就会是128、64、32、16、8、4、2,以此类推。


图9. 32点Stockham 基-2 DIT-FFT算法的数据抽取示意(共5级)
结合GPU硬件,共享内存有16个64bit的bank,基-2计算在向量化访问长度为8、4、2、1(为表述方便,把最后一级也加进来,后同)的计算级,带宽利用率都是1/2。如果用基-4作为基本蝶形单元的话,256点计算级数为4级,访存的向量化长度是64、16、4、1,最后两级的带宽利用率为1/4,与基-2计算的4级1/2带宽利用率等效,但计算级数与基-2相比减少一半。
相比Cooley-Tukey方法Stockham FFT在GPU上实现,可以避免倒序计算和倒序存储两个重要问题。而且CUDA的线程以32个为最小单位同时执行,是向量化的处理机制,Stockham FFT中各级数据的向量化访问,非常适合用GPU来实现。虽然也有存储冲突问题,但在当前架构下基-4计算的(8-2)/24的冲突是可以接受的,剩下的时间可以完成FFT计算。GPU拥有寄存器、共享内存、片外显存的存储层次,Stockham计算的非原址问题并没有影响。在两级计算过程中,线程有足够的寄存器资源把共享内存中的数据全部读出,并行计算,再放回共享内存。
所以本文在GPU上的FFT算法实现,采用Stockham方法。下一节将会叙述Stockham FFT的CUDA实现。
4096点STFFT基本实现
计算框架与工程方法
《Maxwell硬件架构与编程方法》中介绍过Maxwell架构下,每个大核心(SMM)内部有128个小核心(Core)、65536个32bit的寄存器文件(Register File)和96KB的共享内存空间(Shared Memory)。在软件层面,每个线程(thread)最多使用256个寄存器,每个线程块(blcok)最多分配1024个线程,最多占用65536个寄存器和49152bytes的共享内存。
49152bytes共享内存可存储12288个单精度浮点数据(FP32,4bytes),6144个复数(两个FP32)。由于FFT有多级数据交换,为了保证算法的运行时间,数据要放到片上计算,所以考虑到存储能力,理论上一次可以计算4096点。故从共享内存看,每个block需要32768bytes空间,一个大核心可以保证3个block的占用。
寄存器方面,为了4096点计算同时进行,需要8192个32bit寄存器用于数据存储,数值计算过程也会占用寄存器资源,后续还会说到寄存器占用情况和优化方法。实际上寄存器还有盈余,所以8192点的计算也可以勉强在片上一次性完成计算。
由上述架构特点和前一节的理论分析,采用如下计算框架:
- 基-4作为基本蝶形计算单元,6级基-4完成4096点的Stockham FFT计算。
- 每个block分配4096*8bytes = 32768bytes的共享内存空间用于级间数据交换。
- 每个block分配256个线程,为同时计算4096点数据,每个线程一次读取16点数据进行处理。
《Computational Frameworks for the Fast Fourier Transform》书中2.4.4节有Stockham 的基-4算法(书P105,PDF的第123页):
//201710回忆
//L*=L/4,应该是一个R4在L的组内抽取跨度
//r=n/L,是大组数
//W是按组内算的,所以中循环j
用C语言实现的代码较长,本文简介方法。
在C语言验证工程中,首先用递增数给序列赋值,再新建一个txt文件,调用stockham_fft_R4子程序完成计算后,
把结果放到txt文件中。
1 | for (int i = 0; i < len; i++) |
在MATLAB中用同样的方法调用库函数fft()得到结果,把C语言工程的结果导入MATLAB,对比两个序列的相关系数、标准差和序列的插值,进行计算结果验证。
1 | clear all; |
本文在子程序stockham_fft_R4()的基础上设计了一个把各级FFT计算中的数据抽取索引,旋转因子计算索引打印到txt文档中的子程序stockham_fft_R4_index()。这样可以直观快速地查看数值计算过程,本文的后续实现也大量使用这种方法。
CUDA实现
C语言验证
GPU端分配一个256线程的block进行计算,每个线程每次负责16个数据的计算,占用32768bytes的共享内存空间。每一级计算的数据抽取方式都不同。为尽快尝试和验证算法,本文首先在CPU端用的C语言模拟GPU的多线程并行情况,得到正确结果后再移植到CUDA C工程中。
输入序列首地址data_in,相同大小的暂存空间首地址data_out和计算方向direction(正向FFT计算,-1)。首先声明自动变量,index用于保存访存下标索引,wi_c和wi保存旋转因子的浮点和复数数据,16个Complex变量用于保存每个线程读取的16个数据。
1 | void StockhamR4_FFT_4096(Complex *data_in, Complex *data_tmp, int direction) |
下面是4096点FFT的第1层计算代码,一共6级计算,基本保持这样的形式。
通过256次for循环模拟256个线程的并行计算,变量tid代表线程号。
从序列data_in中抽取数据,由于非原址的结构,计算完成后为避免覆盖其他位置的数据,将结果存到data_tmp中,下一次再从data_tmp取数,计算后存到data_in……以此往复,直到计算完成。
寄存器r1,r2,r3,r4中保存的是一个基-4蝶形单元的数据,在第一级,4096点按基-4抽取,跨度4096/4=1024。所以同一个tid的r1,r2,r3,r4地址偏移按1024递增。第一组的4个数据抽取,在并行情况下256线程实际抽取了4096点数据的4个1024数据段中的前256个数据。所以之后的r5,r6,r7,r8在读取数据时,索引要加上256,以此类推。
读取数据后,每个线程计算4组基-4单元。这里调用了基础模块StockhamR4_block(),传入4个数据和1个旋转因子的地址,传入计算旋转因子需要的两个常数wi_c和index(根据线程不同,index不同;根据计算层级不同,wi_c同),图19中第一层旋转因子的基本常数wi_c是 -2π/4 ,而索引index都为0。
计算层级基本保持这一形式,由于数据存储方式不变,之后的示例仅截取for循环的前半部分进行说明。
1 | ////Level in 4//////////////////////////////////////////////////////////////// |
按理论分析,第二层级以1024点为计算单元,还是基-4抽取,1024除以4,跨度是256。同理,第三层级计算单元为256点,内部跨度64;第四层级计算单元为64点,内部跨度16;第五层级计算单元为16点,内部跨度4;第六层级计算单元为4点,内部跨度1。
本文的设计是256线程并行,所以下面第二层级的数据抽取恰好是256*4个变量存一个1024计算单元,变量1-4、5-8、9-12、13-16分别是第1、2、3、4个1024计算单元内的基-4一组蝶形运算,对应旋转因子计算索引0、1、2、3。层级的旋转因子常数是-2π/16。
1 | r1 = data_tmp[tid + 1024 * 0 + 256 * 0]; |
第三层计算单元为256点,内部跨度为64点。并行的线程数是256,如果还是一次读取连续的256点,每个线程只能得到单元内的一个数据,不能计算,所以需要根据线程号来划分各自的计算区域。256点(计算单元长度)除以4(基-4计算变量个数)得到64,所以连续的64个线程负责一个256单元的计算。由于一共有16个变量,所以64个线程计算了4组256单元。整体情况是256个线程前4次读取了1024点数据,4组连续的64线程分别负责4块256单元的计算,后面3组4变量读取按照这种形式分别进行了1024点的计算。
如下面程序所示,与上两层计算不同,第三层首先计算了数据抽取索引index。线程号tid的范围0-255,tid&(256 - 64)可以得到0、64、128、192四个数,即以64为单位将线程分为4组。每组线程负责256点的计算,所以 (tid&(256 - 64)) 4得到0、256、512、768。然后加上tid%64得到线程的组内序号。在读取数据时,以索引index为基地址,进行偏移即可,第三层级计算跨度为64,可以从图21看到读取方式符合这一形式。
第三层有16个256计算单元,所以基-4计算索引根据64线程组和4变量组得到:index = tid/64 + 4(0 or 1 or 2 or 3)。
1 | //64threads 一组 |
根据之前的分析和第三层级的规律,容易得到之后层级的计算结构。要注意的是,共享内存有32个32bit的bank,到第四层级计算单元长度是64,基-4的计算跨度是16(16个64bit数据),恰好还能满足全带宽访问。
1 | index = (tid&(256 - 16)) * 4 + tid % 16; |
第五、六层的16点计算单元、内部跨度4和4点计算单元、内部跨度1都只能占用1/4的带宽(3/4 bank conflict)。
1 | ////Level 1024//////////////////////////////////////////////////////////////// |
还要注意,第六层的计算结构与前面几层不同,一个线程负责连续4点数据的计算,所以读取索引是tid4+1024(0 or 1 or 2 or 3)+(0 or 1 or 2 or 3)。其他部分还是延续规律。
1 | r1 = data_tmp[tid * 4 + 1024 * 0 + 0]; |
CUDA C实现
根据C语言验证结果,把程序移植到GPU端,用CUDA实现。考虑到复用,将4096点的计算封装为一个inline模块,在编译时,模块会“嵌入” 到被调用的地方,而不是跳转调用。函数及参数声明如下,传递的是寄存器地址和共享内存首地址data_shared:
1 | static __device__ inline void Stockham_4096_block |
总结第2、3、4、5层的数据抽取和计算规律,可以把这几层用一个for循环实现,如图26所示。要注意的是,数据的读取和存储都在共享内存上操作,所以在计算完成后需要调用线程同步API __syncthreads();(第30行),等所有线程都计算完成后,才一起把数据放回共享内存,以免覆盖了其他线程的计算数据。为保证for循环下次读取数据的正确性,在数据放回后后也需要进行线程同步。
1 | ////Level 16 64 256 1024/////////////////////////////////////////////////// |
此外,将计算模块进行for循环优化,可以减少寄存器资源占用。从目前的实际情况来看,即使不存在依赖,代码编译后寄存器的占用和代码长度成正相关。所以应尽可能把层级计算整合到for循环里,以减少占用。 只要单个线程的寄存器占用在80左右,在本文的情况下,就可达到每个大核心3个block的最大占用。
优化前寄存器占用在100个左右,只能达到2个block的占用,优化后寄存器占用降到46个,提升明显。
最后,本文把大量使用的Stockham基-4蝶形计算单元封装为inline模块,也就是将stockham_fft_R4()中的核心循环:
1 | for (int j = 0; j < L_d4; j++) |
模块化为:
1 | static __device__ inline int StockhamR4_block |
基-4蝶形单元具有很好的计算特性,涉及的旋转因子复数乘法比基-8和基-16单元少很多,每个线程负责16个数据,也就是4个基-4单元的计算,实际测试结果表明,计算很好地掩盖了访问共享内存的延迟,本文实现的4096点FFT计算时间与cuFFT一致(这里是8192组4096点1维FFT计算时间测试)。
cuFFT结果 : 3.614ms
本文实现结果 : 3.600ms
本文运行环境是WIN7 x64 + CUDA 7.5。
大点数FFT的计算方法
根据GPU硬件和FFT多级数据交换的特点,为了保证算法的运行时间,不能把FFT的数据交换放到显存里,尽量通过片上的共享内存进行。由于存储资源限制,理论上一次可以计算4096点(详见前述)。所以在实现大点数FFT时,首先想到的是把序列分解为多个4096点DFT,再用Stockham方法实现DFT的快速计算。
当序列长度n为复合数时,可以分解为一些因子的乘积,即混合基算法的基本原理。比如,128点的序列,用基-2算法需要7级计算,用基-2/4混合基的话需要3级基-4和1级基-2计算,减少了数据交换次数。在此,本文已经高效地实现了4096点FFT计算,所以可以将大点数序列分解成n=n0*4096的形式计算。
下面先说明混合基算法原理:
一维离散傅里叶变换被描述为: $\quad X_{k}=\sum_{j=0}^{n-1} x_{j} \omega_{n}^{j k}, 0 \leq k \leq n-1$
其中 $\omega_{n}=e^{-2 \pi i / n}, i=\sqrt{-1}, \mathrm{n}$ 是 $\mathrm{FFT}$ 的序列长度,且 $\mathrm{n}$ 具有因子 $n_{0}$ 和 $n_{1}\left(n=n_{0} \times n_{1}\right)$.
$\mathrm{j}$ 和 $\mathrm{k}$ 可以表示为:$j=j_{0} \times n_{1}+j_{1}, k=k_{1} \times n_{0}+k_{0}$
$x$ 和 $X$ 可用二维数组来描述:
$x_{j}=x\left(j_{0}, j_{1}\right), 0 \leq j_{0} \leq n_{0}-1,0 \leq j_{1} \leq n_{1}-1$
$X_{k}=X\left(k_{1}, k_{0}\right), 0 \leq k_{1} \leq n_{1}-1,0 \leq k_{0} \leq n_{0}-$
将上述式子带入离散傅里叶变换公式: $\quad x\left(k_{1}, k_{0}\right)=\sum_{j=0}^{n-1} \sum_{j_{0}=0}^{n_{0}-1} x\left(j_{0}, j_{1}\right) \omega_{n_{0}}^{j k_{0}} \omega_{n}^{j k_{0}} \omega_{n_{1}}^{j k_{1}}$
式(4-1)包含两步多重 FFT 计算。
第一步先计算 $n_{1}$ 次 $n_{0}$ 点 $\mathrm{FFT}$, 并将结果乘以一组旋转因子 $\omega_{n}^{j k_{0}}: \quad X_{1}\left(k_{0}, j_{1}\right)=\omega_{n}^{j / 1 / 0} \sum_{j_{0}=0}^{n_{0}-1} x\left(j_{0}, j_{1}\right) \omega_{n_{0}}^{j / 6_{0}}$
第二步计算 $n_{0}$ 次 $n_{1}$ 点 FFT: $\quad X_{2}\left(k_{0}, k_{1}\right)=\sum_{j=0}^{n-1} X_{1}\left(k_{0}, j_{1}\right) \omega_{n_{1}}^{j / 1 / 1}$
最终得到:
$$
X_{k}=X\left(k_{1}, k_{0}\right)=X_{2}\left(k_{0}, k_{1}\right)
$$
以16384点DIF-FFT为例分析计算结构
16384=4*4096,n=16384,n0=4,n1=4096;j0=(0,3),j1=(0,4095);k0=(0,3),k1=(0,4095)。
先按基-4抽取(每隔4096点抽一个数据)做4096组4点DIF-FFT,按所在序列乘以对应的,即的。
再计算4组4096点FFT得到结果。
从数值计算的角度分析运算过程:
4096组4点FFT计算时,要注意,数据抽取是在16384点数据中以4096为跨度进行的(基-4抽取)。
由于是DIF-FFT计算结构,这里的基-4计算要按DIF的方式进行。
DIF-FFT的数据是顺序进,倒序出,所以在12行乘以旋转因子的时候是乘以倒序的旋转因子。
为了得到顺序的4块4096序列,计算结果的需要按照倒序放回(17行)。
由于在基-4计算中序列按MOD4抽取,所以在进行4组4096点FFT计算后,
要把4块数据进行合并才能得到数据的16384点FFT计算结果(25-29行)。
计算可以分为3个部分:4096组4点FFT计算,4组4096FFT计算和数据的抽取合并。用CUDA C实现的话,考虑到片上存储能力,每部分计算都要做成一个核函数(kernel),耗时是小点数的3倍,和官方库cuFFT两倍左右的耗时有较大的差距。
3个部分中包含大量计算的是中间的4组4096点FFT处理,最后一部分仅改变了数据位置。问题的关键在于,用DIF分解方式可以2步得到FFT计算结果,但这个结果的是分散在n0个数据块中的。如果要降低算法时间,一个可行的办法是结合第2和第3步,将第2步的数据跨越式地存存储。但用GPU实现时,跨越式地把数据存到显存中,会大大降低带宽利用率。要解决这个问题,就要构造出可以在与显存进行数据交换时可以连续访存的算法结构。经测试,使用单精度复数作为数据类型时,还需要保证数据的首地址对齐(128bytes的倍数)。
128bytes/8bytes = 16,即一个warp线程与显存数据交换的最小数量时16个单精度复数,那么底线就是32个线程(一个warp)中前16个线程和后16个线程访问的显存位置可以不一样,但在16个线程中,它们访问的数据必须是连续的,且首地址对齐128bytes。为达到这一要求,在FFT框架下即每次至少要计算16个数据块(因为,在DIF计算完成后,16个线程的数据是从不同数据块的对应位置抽取的),而当前GPU架构每次可以计算4096点数据,所以需要把大点数序列划分为以256为计算单元的多个数据块。比如16384点,就要划分为64组256点FFT,每次抽取16组到片上计算。
受到这些约束,16384点FFT计算的实际分解方式是:
16384=64*256,n=16384,n0=64,n1=256;j0=(0,63),j1=(0,255);k0=(0,63),k1=(0,255)。
先按基-64抽取(每隔256点抽一个数据)做256组64点DIF-FFT,按所在序列乘以对应的,即的。
再计算64组256点FFT得到结果(在GPU上实现,有更细的划分)。
以上是理论说明。
65536*4以上大点数的处理方法
1 | 本节作为附加介绍 |
为了实现更快速度,在FFT+点乘+IFFT。这样的频域算法计算中。
结合Cooley-Tukey和Stockham结构,中间结果不要求完全“顺序”:
顺序输入 >> Cooley-Tukey >> 倒序输出
65536*4/4096=64,即256K点数据可以分为64组4096点FFT计算。
先用DIF Cooley-Tukey 拆分4096点数据(见上一节理论和CTFFT计算结构示意图)
可以看出DIF第一级计算以后,8点分治为两个4点计算(即后续的计算两个4点之间没有依赖)
按照4096点Stockham结构,计算64组数据,即可得到FFT计算结果。
注意,此时的数据是按64块倒序存放的(注意描述,按分块倒序,块内数据是“顺序”的)
因为,已经得到结果,为了节省时间,不再用一个kernel得到顺序结果。
点乘。完成频域计算。
进行64组4096点IFFT
利用DIT Cooley-Tukey结构处理64块4096点数据
(在stage0不用倒序,因为数据已经按块倒序了)
所以计算步奏如下:
1 | 1、DIF Cooley-Tukey 拆分数据(顺序输入,按块倒序输出) |
利用Cooley-Tukey FFT的计算结构,拆分大点数计算。
利用Stockham FFT 向量化的计算结构,进行大部分计算。
计算步骤2、3、4可以合并为一个kernel。
整体时间为4个访存密集kernel时间。
1 | 而调用cuFFT的话,从这个数据长度开始 FFT,IFFT都需要3个访存密集kernel时间 |
所以实际工程中,可以加速2倍左右。
1 | 这一方法在本文框架中,可以处理65536*4到65536*256的计算规模: |
时间测试
cuFFT结果 : 3.642 + 3.665 = 7.307ms
本文实现结果 : 4.215 + 3.740 = 7.955ms (稍慢,实际整合频域算法的话,快1/3的时间)
…
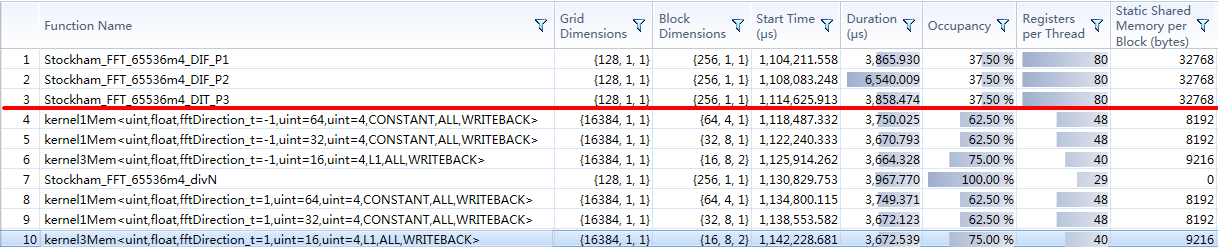
cuFFT结果 : 3.65*6 + 3.65 = 25.55ms (3FFT 3IFFT 1频域计算)
本文实现结果 : 3.85 + 6.54 + 3.85 = 14.24ms (注意,234步骤已整合到第二个kernel)
1 | 补充一点,在这一维数据长度,调用cuFFT,库自己拆分为三个kernel进行计算,非用户操纵。 |
补充公式