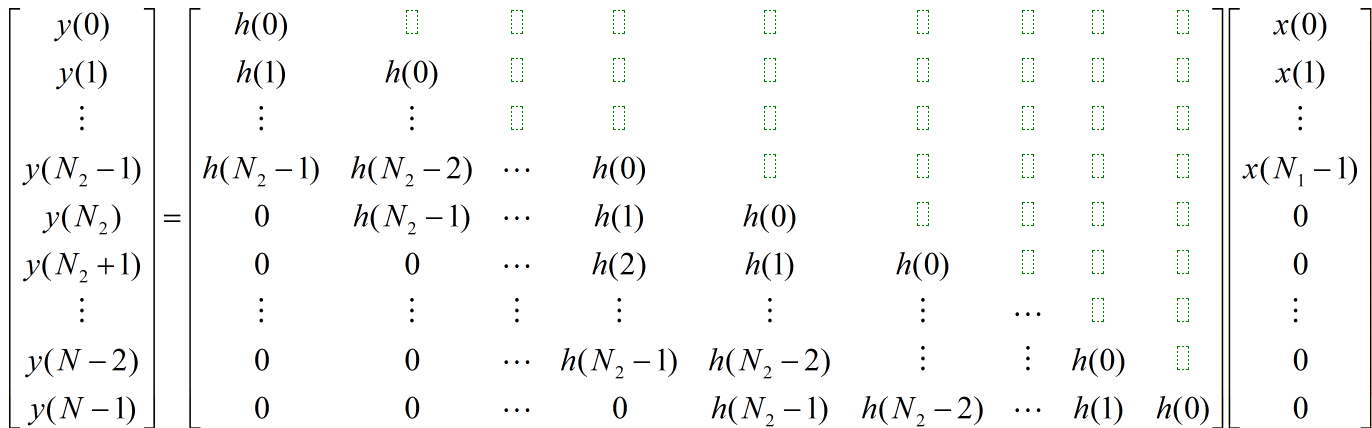本项目使用MaxAs提供的汇编器编写GPU一维卷积算法
有16点和1024点卷积核两种实现，SASS代码在目录下，两个VS2013工程在文件夹中
实验环境：WIN7 + VS2013 + CUDA 6.5 + MaxAs (SASS代码已注入cubin，运行不需要MaxAs)
16点卷积和1024点卷积恰好可划分在访存密集和计算密集这两个类型中，是比较好的练手项目。
1024点卷积在Maxwell架构下达到硬件75%的峰值算力，还在找未达到90%以上的原因。
1、一维卷积计算过程
线性卷积: $y(n)=x(n) * h(n)$
设x(n)长度为N1，h(n)长度为N2 ， 则y(n)长为 N=N1+N2-1
为方便表示，在序列x(n)后添N2-1个0 ，使x(n)的长度变为 N
卷积公式 ： $y(n)=\sum_{i=0}^{N-1} x(i) \times h(n-i), \quad 0 \leq n \leq N-1$
可用矩阵表示为：
一个简单的计算过程示意：
x(n)=[4,3,2,1]
h(x)=[3,2,1]
y(n)=x(n)*h(n)
1 | x | 4 3 2 1 | |
为保证局部性：
在实现时，卷积核H的数据先放到片上
（H点数较小时直接放到寄存器，点数稍大可放在共享内存，过大时分批从片外内存读取）
实际的原始数据X，点数较大，分块（blocking）处理。
Y的计算不按照上例中的一次性计算$y^2=4 1+32+2*3=16$ 。
而是 多次乘加 得到结果 ：
1 | //Y初始化为0 |
上例每次读一个X。实现时，X批量读入，计算掩盖访存延迟。
2、两个实现：16点卷积与1024点卷积
算法分析
| 算法 | 卷积 |
|---|---|
| 数据量 | N*2 (输入X / 输出Y / H较小不计入) |
| 计算量 | N*N2*2 (乘加按两个指令计算) |
| 硬件 | GTX970 |
| 峰值计算能力 | 1.25GHz 1664cores 2 = 4160 GFLOPS（实测达到） |
| 访存带宽： | 224GB/S （实测连续访存140GB/s ，即35G/s的FP32数据） |
算法计算强度 $=\frac{\text { 计算量 }}{\text { 数据量 }}=\frac{2 N N 2}{2 N}=N 2$
(即一维卷积计算算法强度与卷积核长度直接相关： 16点卷积计算强度为16， 1024点卷积计算强度为1024)
硬件计算强度 $=\frac{\text { 浮点计算能力 }}{\text { 浮点带宽 }}=\frac{4160 \mathrm{GFLOPS}}{35 \mathrm{GFloatData}}=118.8$
所以16点卷积计算 ：受限于带宽 （16 < 116.8 访存密集）
1024点卷积计算 ： 受限于核心计算能力（1024 > 116.8 计算密集）
所有算法都可以从这一角度，划分为上述两个类型之一。
计算密集的算法，可以针对硬件架构进行优化。
16点卷积
一维卷积核H：16 float （直接拷贝到寄存器）
输入数据量X：1024000 float
输出数据量Y：1024000 + 16 float （最后16个Y为了方便，没有进行计算）
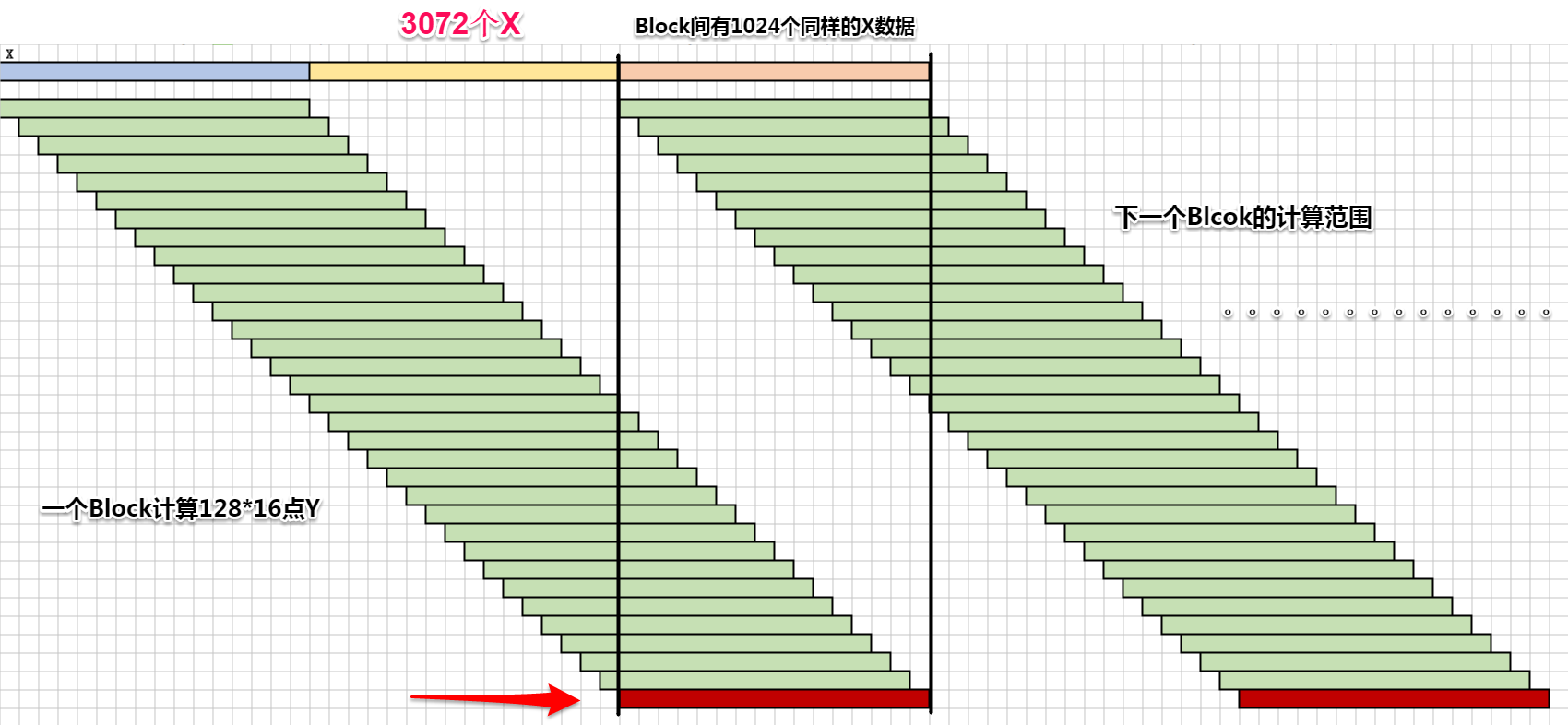
线程结构 : 32个thread一个blcok，每个thread计算16点Y，一共需要2000个block。
片上存储 ： 分配544 float * 4 bytes = 2176 bytes 大小的共享内存空间用于存储。
存储结构
Shared存储
每个block负责32*16=512点Y计算
32个threads 对显存合并访问 读取X
每个thread进行4次LDG.128访问 + 一次LDG访问（32bit，末尾的32个X，只用到1/2的数据）
Shared访存
整体来看，一个线程需要访问8次共享内存（128bit形式）
eg：
第一次，所有线程访问第一行，第二次第二行，第三次第三行，第四次第四行
第五次时，需要向左移一列访问，接下来再访问三行
（注：图看不清的话，可以点击放大）
以thread 0为例 ，蓝色框是其访存范围，红色线条是访存顺序。
黑框是 thread 1 的访存范围，前后两个线程共享16个 float 数据
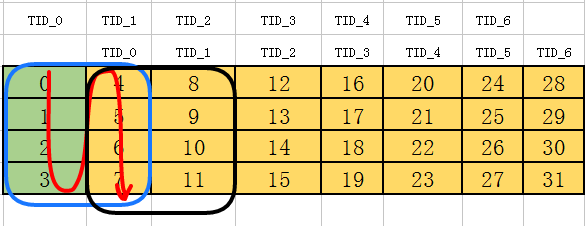
这样的LD/ST方法，利用了完整的共享内存带宽。
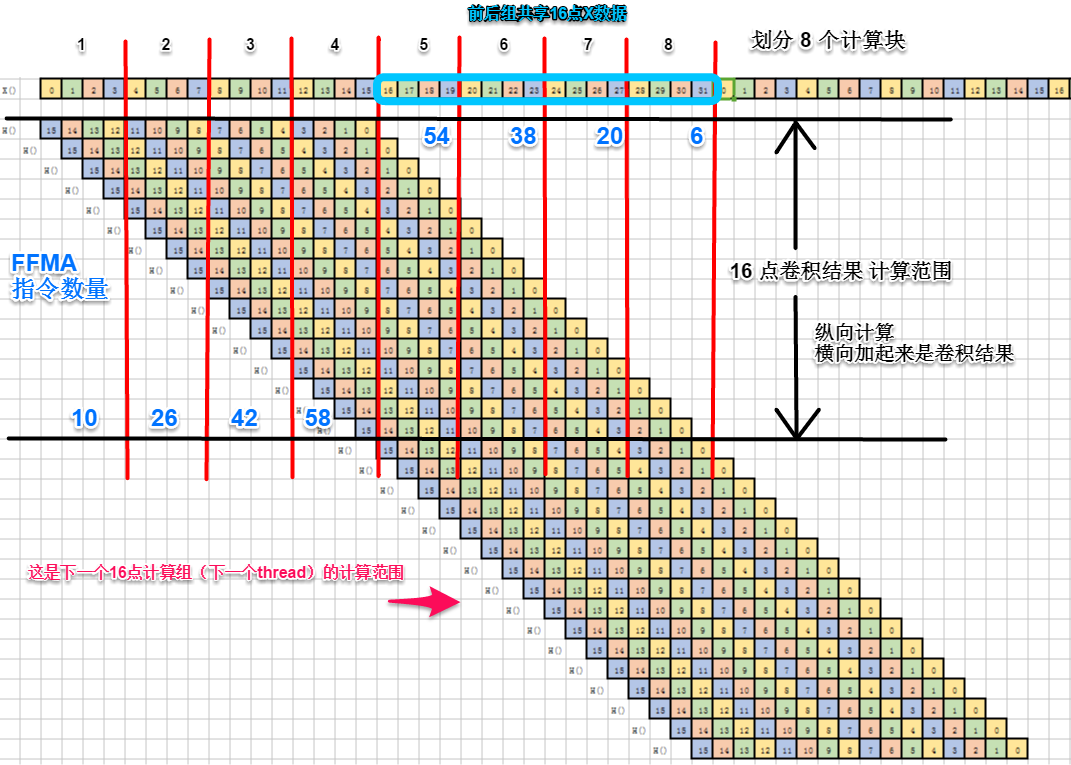
算法结构
计算示意（结合 1、一维卷积计算过程 理解）
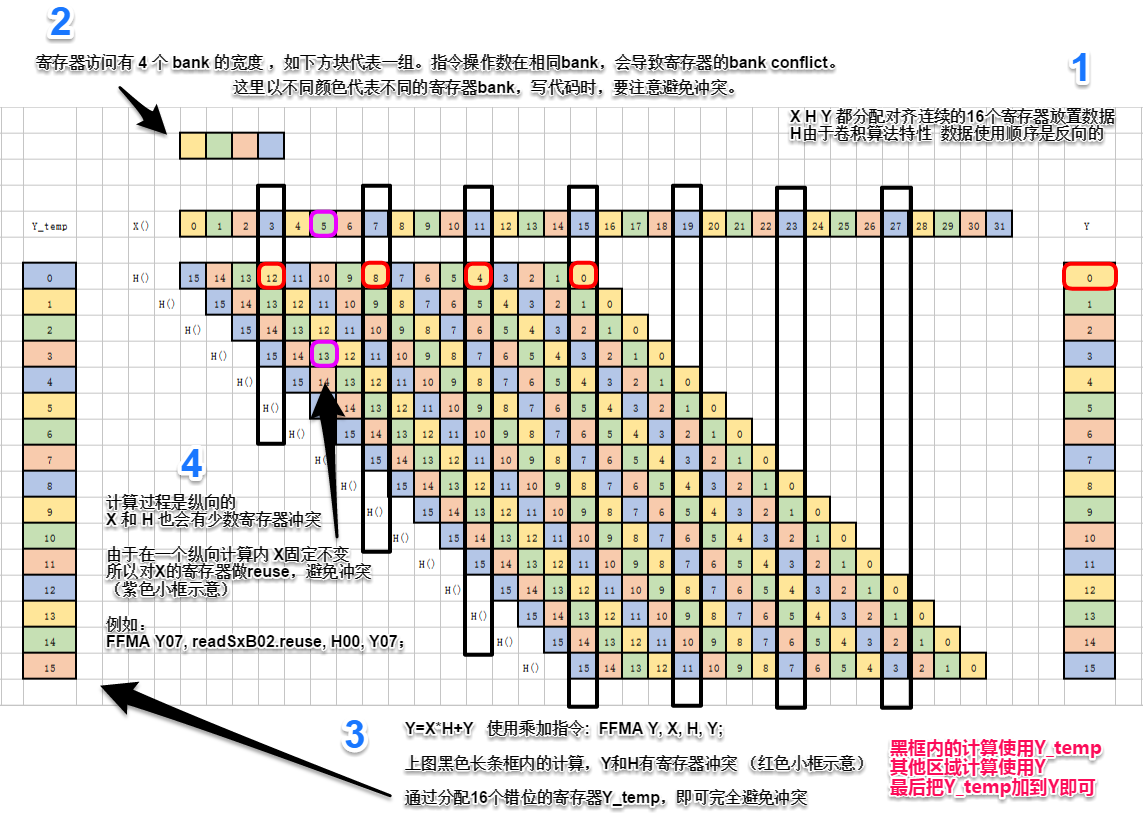
完全避免寄存器冲突的办法
1024点卷积
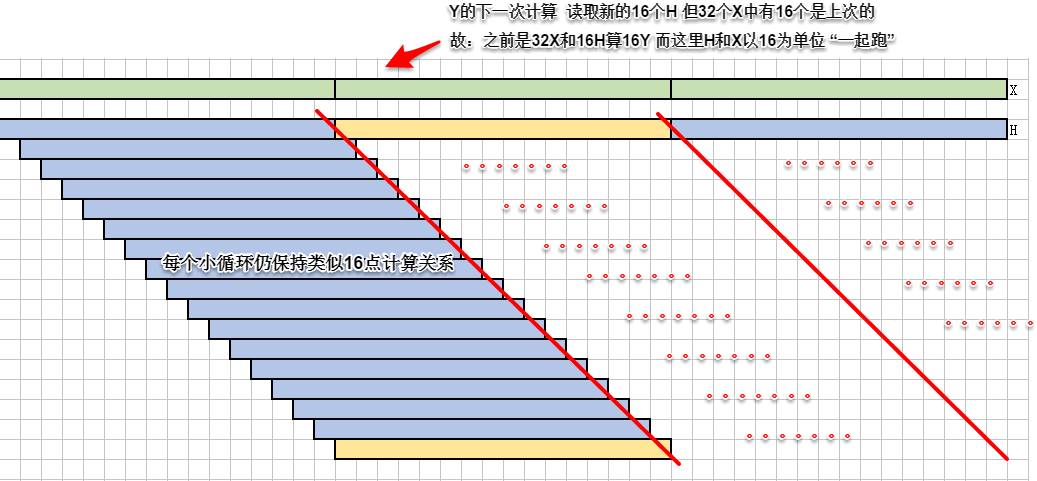
计算的核心循环与16点卷积一致，32点X与16点H参与计算。
区别在于下一次循环还要使用32个当前计算X中的的后16个；下一次计算使用的H是新的16个。
理论分析：由于一个小循环算完16点Y，数据都在片上，所以再套上大循环，对X、Y做双缓冲不会有速度提升
实际处理：H加双缓冲无效，寄存器双缓冲预取共享内存中的X，计算掩盖延迟。
一维卷积核H：1024 float
输入数据量X：2097152 float
输出数据量Y：2097152+1024 float （最后1024个Y为了方便，没有进行计算）
线程结构：128个thread一个blcok，每个thread计算16点Y，一共需要1024个block。
存储结构
X数据存储与16点类似，一个block存128线程(4float6次加载)=3072个单精度浮点。
还需要10244byes存放H。
共分配40964bytes的共享内存空间
计算结构
block内计算示意
block间计算示意
注:Y存回片外时通过共享内存reshape，有bank conflict，只用到了共享内存1/4的完整带宽。
但实测对kernel执行时间基本没有影响（占比太小）。
SASS代码：
conv1024_nobuffer.sass
3、实验结果
16点卷积
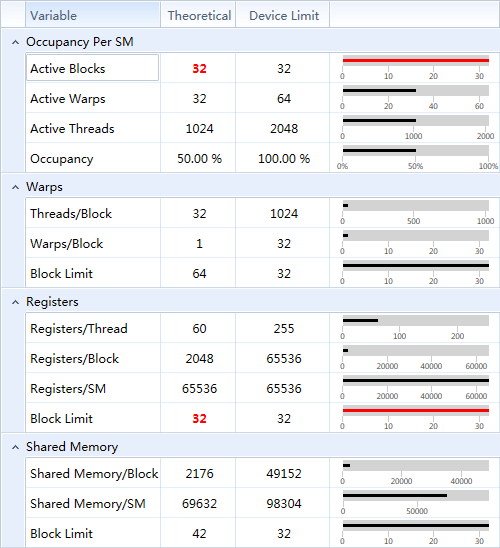
每个线程使用60个寄存器（优化后），恰好达到1个SM上32个Block的占用上限。
实测，只要一个SM上达到6个Block的占用，就可占满带宽。
6占用kernel执行时间和32个占用的时间一致。
占用多了，带宽跟不上，还是需要等待。
数据量(32*16*2000)*2 = 2*1024000FP32 = 2*1024000*4bytes/1024/1024 = 7.8125MB
下图可知，kernel平均计算时间为56us
带宽占用： 7.8125MB / 0.056ms = 139.51GB/s
与理论分析一致
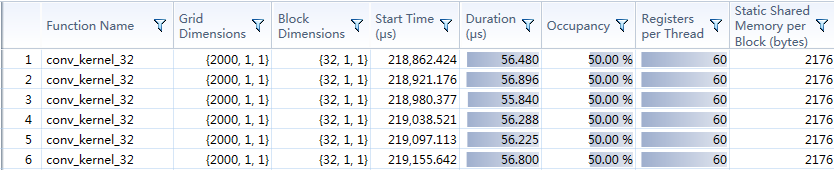
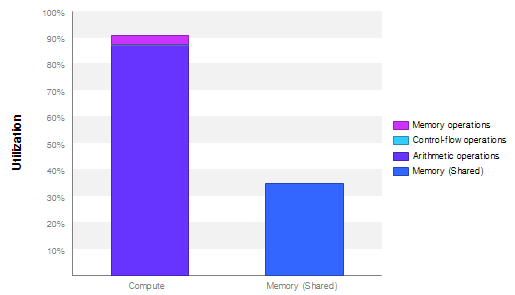
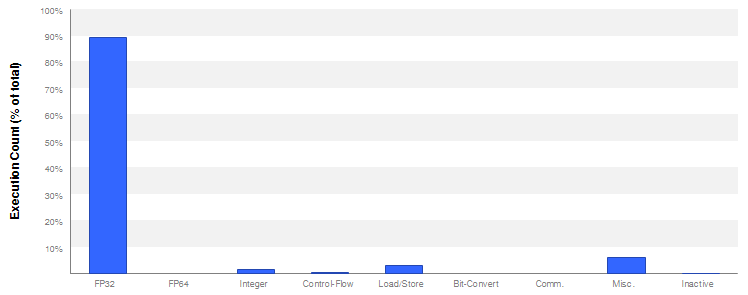
1024点卷积
Visual Profiler （nvvp）分析：
带宽未占满
计算指令占比接近90%
SM占用6
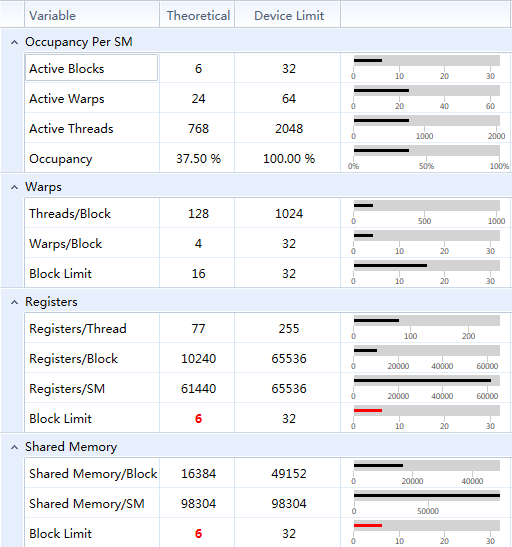
实测占用 6、4、2个block的情况，kernel执行时间一致。
由于计算能力限制，占用多了也算不过来。
kernel执行时间1.4ms
| 结果 | 达到硬件峰值计算能力的74% （未达到90%） |
|---|---|
| 数据量 | 输入X+输出Y = 22097152 float = 22097152*4bytes/1024/1024 = 16MB |
| kernel时间 | 1.4ms |
| 带宽占用 | 16MB / 1.4ms = 11.42GB/s |
| kernel算力 | 2097152_X输入1024_H卷核2_乘加 / 1.4ms = 4.295 GigaFloatOp / 0.0014s = 3067.86 GFLOPS |
| 硬件算力 | 1.25GHz 1664cores 2 = 4160 GFLOPS |
数据生成及结果验证
原始数据X、卷积核H和结果Y的长度分别为N、M、P。
卷积核与原始数据用伪随机数填充。
CPU计算的卷积结果放在数据块T中。
GPU计算的卷积结果拷贝到数据块Y中。
打印前1024个T与Y的误差
Y与T差的绝对值大于1则打印出来（计算精度所在位置随数据大小变化）
4、小结
常用的优化方法：
调整算法结构（匹配硬件特性），kernel间整合（减少访存），kernel优化（数值计算过程与汇编）
16点卷积和1024点卷积恰好可划分在访存密集和计算密集这两个类型中。
是比较好的练手项目。
访存密集型的算法不需要用汇编优化，保证基本的合并访存即可。
但一些算法结构复杂，需要仔细分析，利用好片上和片外内存的带宽。
1024点卷积kernel应该达到90%+的峰值算力，未找到受限原因。
理论上1024点卷积不需要嵌套循环，不用对X做双缓冲预取，因为当前计算的Y与下一大组X没有数据依赖关系。
按现在的理解，在SM上block占用低于一个阈值的情况下，双缓冲可以带来一定的计算能力提升。
在占用足够的情况下，线程级并行、线程间的切换，其实和双缓冲是等效的。
（2017补充）
实际工程中常用FFT在频域进行快速卷积。
5、后续
二维卷积
FFT