SEGMM的CUDA Core实现


阅读数: 次   
字数统计: 6.7k字   |   阅读时长: 25分

SGEMM：Single precision floatiing General Matrix Multiply

本文的SGEMM实现思路整理于MaxAs wiki和对MaxAs项目SGEMM汇编代码的理解。
MaxAs是一个开源的Maxwell架构GPU汇编器： Github链接
作者Scott Gray提到两篇相关论文MAGMA paper和Kepler sgemm paper

定义

​ $A=\left(a_{i j}\right) $ 是一个$ m \times s$ 矩阵, $B=\left(b_{i j}\right) $是一个 $s \times n $矩阵,规定矩阵A与矩阵B的乘积是一个$m \times n$矩阵$,C=\left(c_{i j}\right)$其中$c_{i j}=a_{i 1} b_{1 j}+a_{i 1} b_{1 j}+\cdots+a_{i s} b_{s j}=\sum_{k=1}^{s} a_{i k} b_{k j} \quad(i=1,2, \ldots, m ; \quad j=1,2, \ldots, n)$,把这个乘积记做$C=A B$。

​ 由定义可知，计算一个元素$c_{i j}$的时间复杂度是$O(N)$，矩阵$C$中有$N^2$个数据，矩阵乘法的时间复杂度为$O(N^3)$。

计算示例

$A=\left(\begin{array}{cc}-2 & 4 \ 1 & -2\end{array}\right) \quad B=\left(\begin{array}{cc}2 & 4 \ -3 & -6\end{array}\right)$

$c_{11}=A$ 的第一行 $\cdot B$ 的第一列 $=a_{11} b_{11}+a_{12} b_{21}=-2 \times 2-3 \times 4=-16$

$c_{12}=A$ 的第一行 $\cdot B$ 的第二列 $=a_{11} b_{21}+a_{12} b_{22}=-2 \times 4-4 \times 6=-32$

$c_{21}=A$ 的第二行 $\cdot B$ 的第一列 $=a_{21} b_{11}+a_{22} b_{21}=1 \times 2+2 \times 3=8$

$c_{22}=A$ 的第二行・ $B$ 的第二列 $=a_{21} b_{21}+a_{22} b_{22}=1 \times 4+2 \times 6=16$

即 $C=\left(\begin{array}{cc}-2 & 4 \ 1 & -2\end{array}\right)\left(\begin{array}{cc}2 & 4 \ -3 & -6\end{array}\right)=\left(\begin{array}{cc}-16 & -32 \ 8 & 16\end{array}\right)$

计算结构

朴素算法

解题时的书面计算习惯，通常是在A、B两矩阵中各取第i行、第j列，按照定义点乘累加，计算矩阵C中的一个元素$c_{i j}$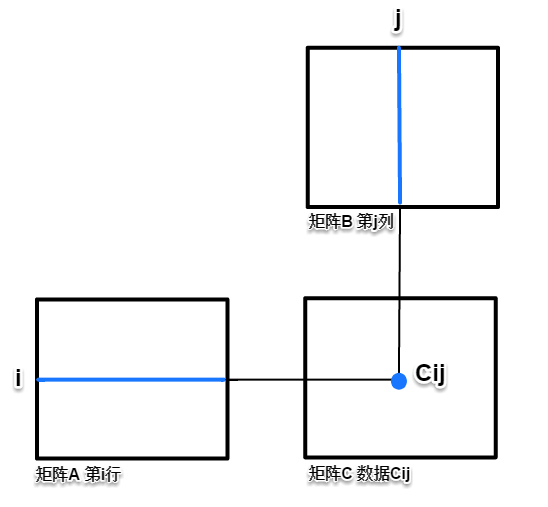

设矩阵A、B和C都是NxN的矩阵，则有朴素算法：

1
2
3
4
5
6
7
for(i=0;i<n;i++)
    for(j=0;j<n;j++){
        sum = 0;
        for(k=0;k<n;k++)
            sum += A[i][k]*B[k][j];
        C[i][j] += sum;
    }

​ 由图示可知，使用朴素算法实现时，不连续地读取矩阵B的一列数据（内存空间数据跨度为N），空间局部性很差。
​ 另外，与$c_{i j}$同行或同列的C元素，都由相同行或列的A、B数据计算得到，但朴素算法每个核心循环只计算一个元素$c_{i j}$，不能重复利用缓存中的矩阵数据（N较大的情况下，还没轮到下一个循环，cache空间已经被新数据占用了，不能命中，A的首次不命中概率为：1/cache字长，B的不命中概率为1），同行、列的数据利用率只有1/N，所以时间局部性也很差。

计算量分析：

​ 设A、B和C都为N阶方阵，则计算一个元素$c_{i j}$的访存量为$2N+1$，计算量是$2N$（乘加按两次操作算）单位访存的计算量为：1

​ 各类硬件的单位片外访存时间 远高于 单位片内计算操作的时间消耗，所以这个计算结构是访存密集的。算法的执行时间受访存带宽限制，大多数时间里，计算单元在等待数据加载。

分块算法

​ 分块（blocking）技术可以提高内循环的局部性（locality）。分块的大致思想是将数据结构组织成的片（chunks）称为块（block）。（在这个上下文中，“块”指的是一个应用级的数据块，而不是高速缓存块。）这样构造程序，使得能够将一个片加载到高速缓存中，并在这个片中进行所需的所有读写，然后丢掉这个片，加载下一个片，依此类推。

​ 不同于为提高空间局部性做简单的循环变换（朴素算法有ijk、jki、kij几类循环方式，内层循环数据加载对应AB、AC和BC，BC加载类型每次迭代的总不命中次数最少），分块虽然在一些系统上能获得很大的性能收益，但也使得代码更难阅读和理解，更适合优化编译器或者频繁执行的库函数。

​ 根据硬件资源，划分A、B、C子块的大小，使它们都能放到片上存储。每取一列A数据和一行B数据，都能计算n*n次C数据，多次取数据点乘累加得到完整的$c_{i j}$数值。对于矩阵C（或矩阵C子块）中的一点，每次读取AB的2组n点数据后，核心计算为：$c_{i j}=a_{i k} b_{k j}+c_{i j}$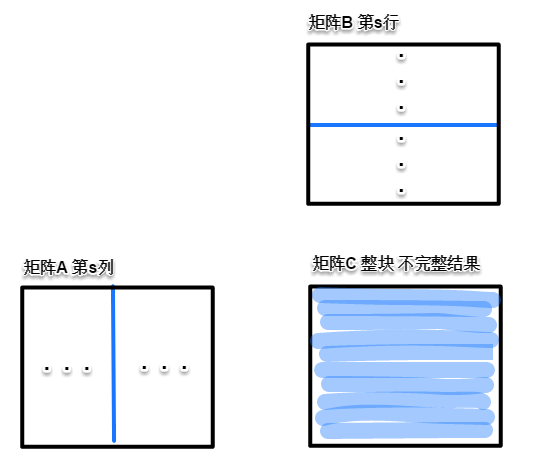

计算量分析：

注：分析针对每个block的核心循环，故按分块，分析小矩阵。

​ 假设A子矩阵大小为$n \times K$，B子矩阵大小为$K \times n$，C子矩阵大小为$n \times n$，则分块矩阵乘法的访存量为$2Kn$（注：在核心循环里不访问C，计算完成后才放回，故不计入$n^2$)，计算量是$n \times n \times K \times 2=2 K n^{2}$，即K组对应的行列都有$2n^2$次计算，乘加计算视为两次操作。

​ 单位访存的计算量为（即kernel的计算强度）：$\frac{2 K n^{2}}{2 K n}=n$,即n取值越大（子块越大），单位访存的计算量越大。n=128时，单位访存的计算量为128.

算法与硬件性能

显卡 GTX970
峰值计算能力 4TFLOPS （乘加实测达到）
访存带宽 224GB/S （实测连续访存140GB/s ，即35G/s的FP32数据）

硬件的单位访存计算能力 = 浮点计算能力/浮点带宽 = 4000GFLOPS/(35G FP32 DATA) = 114.3

1<<114.3<128

所以，就GTX970来说，128分块矩阵的计算需求比硬件能力稍大，可以完整占用计算资源，是很好的实现方式。
属于计算密集算法，需要在算法结构和汇编细节上做优化，才能利用好硬件算力。

MaxAs中的SGEMM实现

按照上一小节的分块算法，构造计算结构，尽可能重复利用从各个存储层次获取的数据。在GPU上，也就是：

显存>>L2缓存>>纹理缓存>>寄存器>>共享内存>>寄存器>>指令操作数缓存>>寄存器>>显存

(其中，指令操作数缓存是Maxwell架构的新特性)
上述的每个数据路径都有延迟，要通过指令级并行和线程级并行（instruction and thread level parallelism ，ILP & TLP）来掩盖。此外，还存在存储单元和合并访存的限制（banking and coalescing constraints）。作者的SGEMM代码可以在这些限制下，使算法的计算效率达到98%的GPU峰值计算性能。

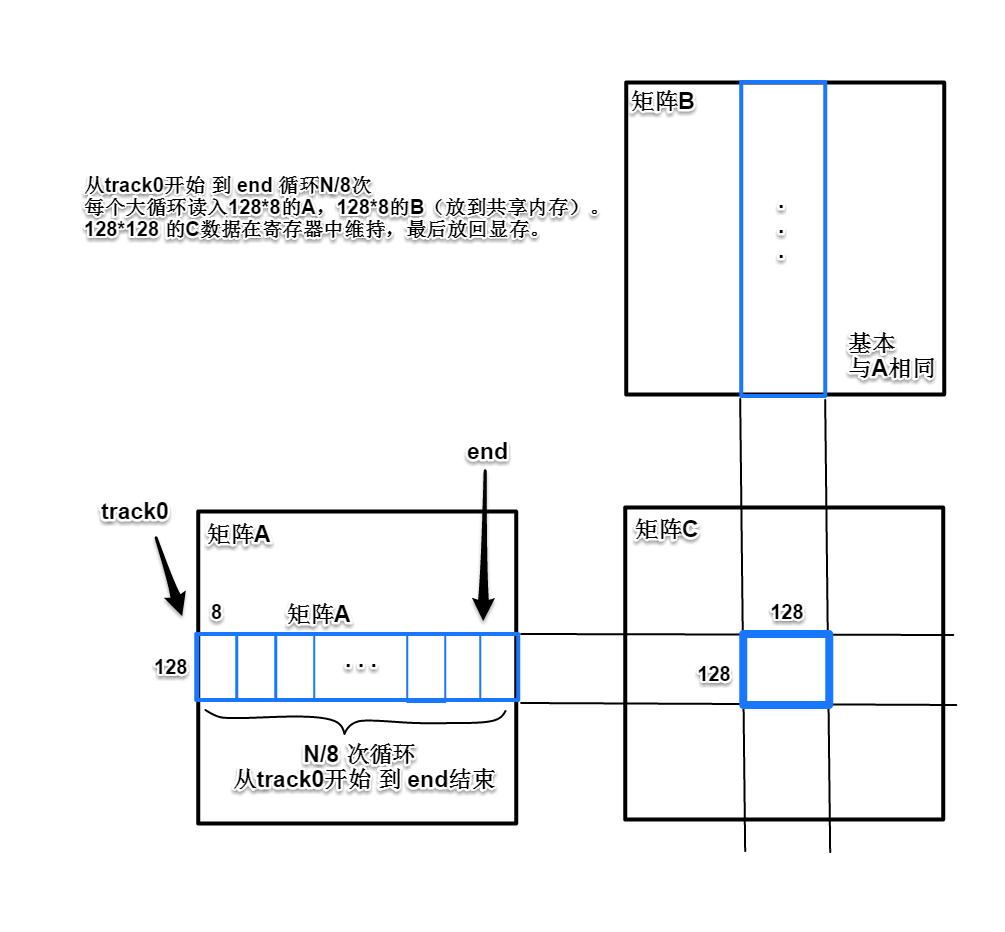
这里，先说一下最终采用的基本计算模型，稍后会解释参数选择的原因。
把A、B矩阵划分为多个128x8的小块，如图所示，将矩阵A中所有横向数据块和矩阵B中所有纵向数据块带入计算，乘加，最后得到128x128的C矩阵子块的结果。一个时间段内，只需要拷贝A、B各一片对应数据块到片上共享内存，计算过程里，128x128点数据的中间结果保存在各线程的片上寄存器里，图中两组蓝色长条数据块都计算完成后，再把矩阵C的128x128子块计算结果放回显存。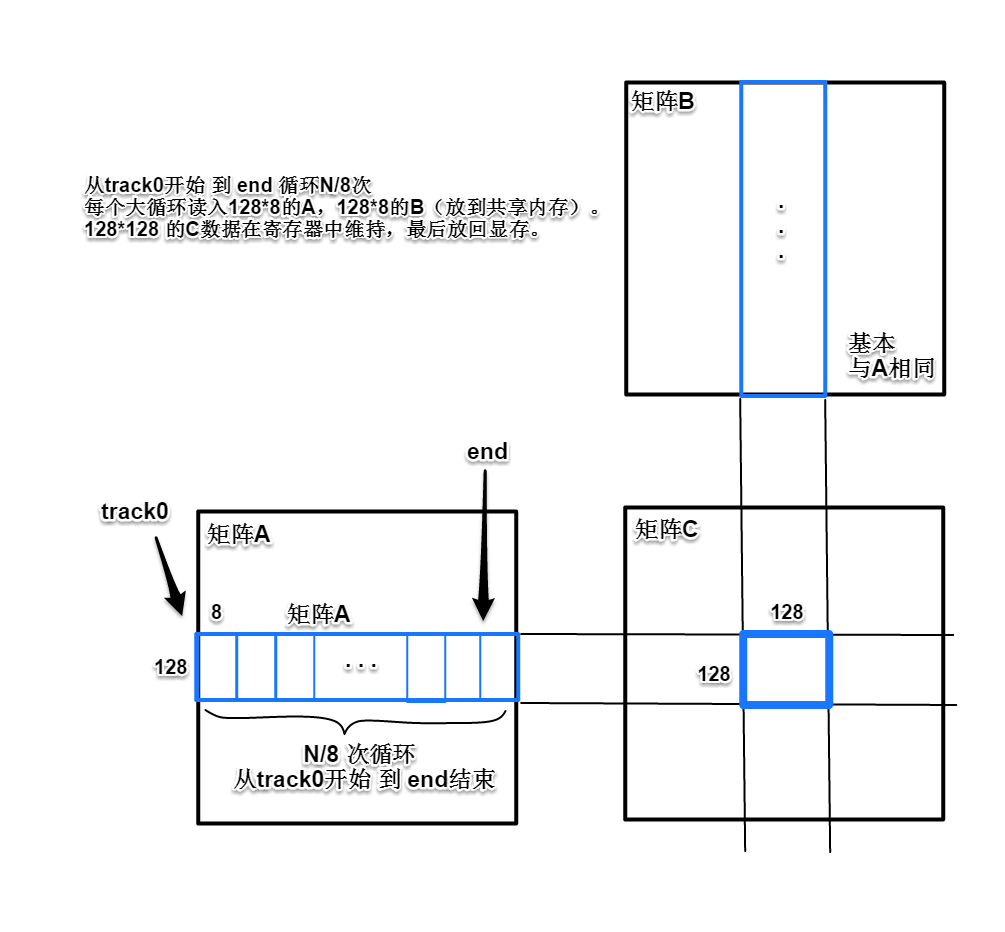

关键结构与参数

双缓冲

使用大小为8的双缓冲寄存器块（double buffered）存放从显存加载的矩阵数据。
双缓冲能基本掩盖数据传输延迟：在计算一组数据的同时加载下一组数据。
寄存器块的寄存器数量设为8，可以配合长度为4的向量化内存加载指令（quad vector memory instructions），同时保证每个线程的寄存器使用数量在128个以下。超过128个寄存器的界限的话，SM的block占用会下降。

对共享内存也做双缓冲处理，这样可以移除一个本来需要的在主循环中使用的BAR.SYNCS：在存
储下一组数据时等待所有共享内存加载完成（按上下文应该是shared加载到reg）。
有了双缓冲以后，数据可以直接写入另一块的共享内存区域，各线程仍可以从之前的共享内存区域读取数据。这样做需要在主循环中增加三条XOR指令，但（时间）代价比BAR.SYNCS小。

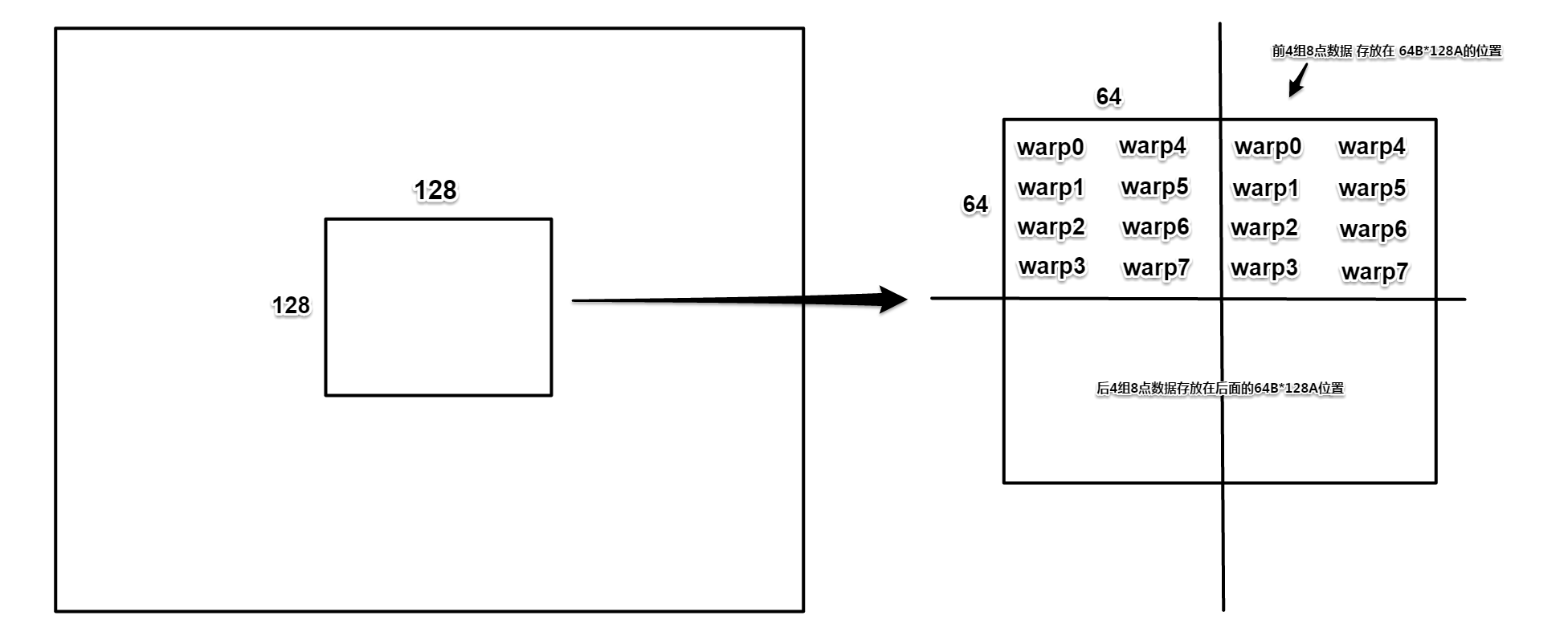
每个block有256个线程，每个线程计算88=64点子矩阵C的数据，
每个block处理一块正方形的子矩阵C，方形的边长就是所有点数的平方根。
可以计算得到：$\sqrt(256*88)$ = $128 units wide$

展开因子

​ 展开因子(unroll factor)对应每次从A和B中读入的行数（global>>shared），也是从共享内存中存储、加载以及计算数据的量。展开因子的选择有两个考虑：一方面希望用尽可能多的计算来掩盖纹理内存加载延迟，另一方面不希望循环大小超过指令缓冲区大小。否则，额外增加的取指延迟，又要想办法掩盖。作者测得Maxwell的指令缓冲区大小为8KB，所以不能让主循环大小超过1024个8byte指令，而且4个指令一组，其中的第4个指令是控制代码（control code），所以实际可用指令数限制为768个。另外还有指令对齐方面的考虑,所以指令数最好低于768。

​ 综上考虑，把展开因子设为8，8*64=512个FFMA指令（浮点乘加）加上循环所需的访存指令和整数计算指令（大约40个），低于768。每个循环8行展开也能较好地配合纹理内存加载，512个FFMA计算足够掩盖200+时钟的纹理内存加载延迟。

共享内存大小

​ 共享内存大小，由每个block的加载宽度乘以展开因子得到。需要256线程：每个循环处理8行，每个block加载宽度128，单精度浮点数据字长4bytes，矩阵A数据双缓冲，矩阵B数据双缓冲 >> 需要$8128422 = 16384$ bytes 的共享内存空间，Maxwell架构下：一个SM有65536个32bit的寄存器，98304 bytes的共享内存空间。
​ 98304/16384 = 6
​ 65536/(256线程*128寄存器) = 65536 / 32768 = 2,也就是说，共享内存大小可供6个block占用，但由于寄存器资源不够，只能得到2个blcok的占用。这里，共享内存的大小不是SM上block占用的主要因素，SGEMM的占用主要受寄存器资源的影响。（占用多不代表算得快，快慢主要受计算和访存能力影响。这里2个block的占用已经足够了）

256线程算法实现

加载A、B到共享内存

​ 作者把线程分为两部分，一半线程加载一个矩阵。256线程的话，就是4个warp（128线程）加载一个矩阵。条件加载在cuda中优化得不好，因为编译器不会判断加载是否以warp为单位而做优化。对于纹理内存加载来说（MaxAs中的SGEMM用了纹理，但相关的开源项目，后来不使用纹理，直接加载global），分开处理是必要的，因为每个warp的指令在一个时间只能处理一个纹理内存（分开加载更高效）。编译器会给纹理加载加入warp切换和分支（warp shuffles and branch），还有同步指令来强制执行。如果Nvidia给出以warp为单位的条件判断结构会很好（而不是仅仅有分支，ie：bra.uni）。

​ 一个线程来只负责加载某一个矩阵，所以只需要一组索引寄存器（track registers）来存放纹理加载的索引。主循环里的整数加法指令因此减少一半，this is a big win 。在核心循环中，要抓住任何提升FFMA指令/非FFMA指令比例的机会。

​ 另外，维持4个单独的索引变量以避免使用依赖栅栏（dependency barriers），每次纹理加载后给索引寄存器加上加一次的地址偏移。在架构上，访存指令发出后，并不会保存它调用的寄存器值，这样做可能是为了节省硬件资源。指令发出后，访存工作仍在执行(in flight)，而地址索引仍保存在一个寄存器中，这就需要用一个栅栏来保证不对相关寄存器进行写入。栅栏等待不一定就是坏事，线程级并行（TLP）可以掩盖延迟，但减少整体的延迟有助于提高性能，提高有可用warp来掩盖延迟的几率。

​ 接下来就是从纹理单元加载。使用显式的纹理加载，而不用全局加载或不连续缓存（?），有两个好处。一是代码更简单，不需要担心加载超出边界。二是，同样的kernel代码可以加载8 bit或16 bit浮点数据，大大减少带宽和存储的需求，对于一些不需要32 bit精度应用很有优势。

​ 此外，对访存做4单位的向量化加载。cublas没有使用向量加载，因为输入数据有4字长对齐的限制，不能适用于普遍情况，cublas有自己固定的形式。使用4点向量化数据加载后索引偏置常数lda和ldb相应减小4倍，附带的好处是加载矩阵的索引可以增加到31bits，而普通纹理加载受限于27bits。另一个vec4加载的效果是，这一访存模式每次读取都占用整个缓冲区，缓存性能主要受L2限制（这点不太明白）。

从共享内存加载数据到寄存器

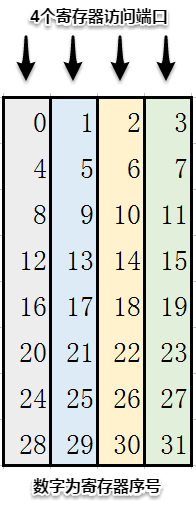
​ 每个线程从共享内存的A、B区域读取数据，原则是避免bank conflict。根据文档，只要访存在32字长（128bytes）以内即可。warp内各线程进行vec4加载，某几个线程从相同地址加载，通过广播机制，可以在128 btyes的限制下读取数据。Maxwell的文档说明并不完整，在一些情况下，即使一个warp中的线程访问的数据在128 bytes以内也有触发存储冲突的情况（理论上，Maxwell架构的共享内存有32个32bit端口，同时读取的数据超过128 bytes带宽，就要排队等待，同时读取的数据占用相同端口，也要排队等待，即访存冲突。另外，实测warp内不连续或不同深度的访问，时间也会增加）。

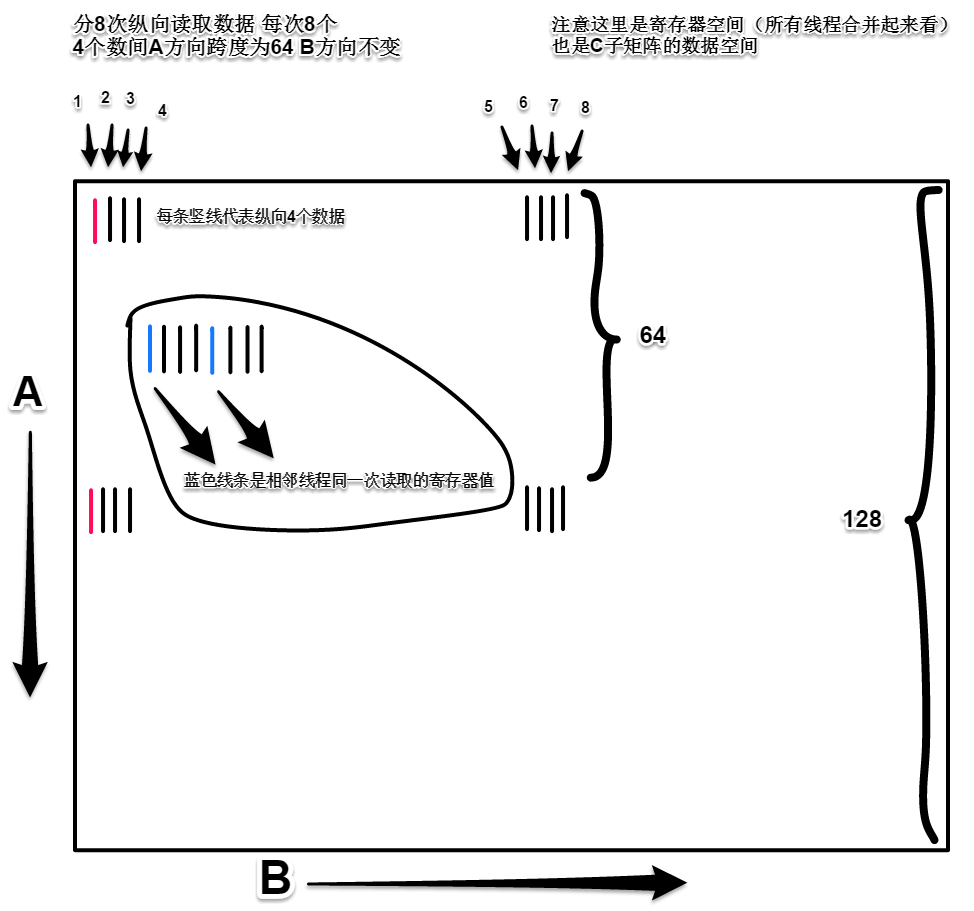
​ 128 bytes带宽可供加载8组16 bytes的4点向量化数据(vec4)。在这一限制下从A、B共享内存中加载。每次从共享内存块加载的宽度为4*64=256 bytes，所以把加载分为为两次，第二个加载指令跨度为64个数据。把这两个一维加载构造为二维，得到加载后线程寄存器空间与C子矩阵数据空间的对应关系，即C子矩阵数据在每个线程的64个寄存器中的存放位置：

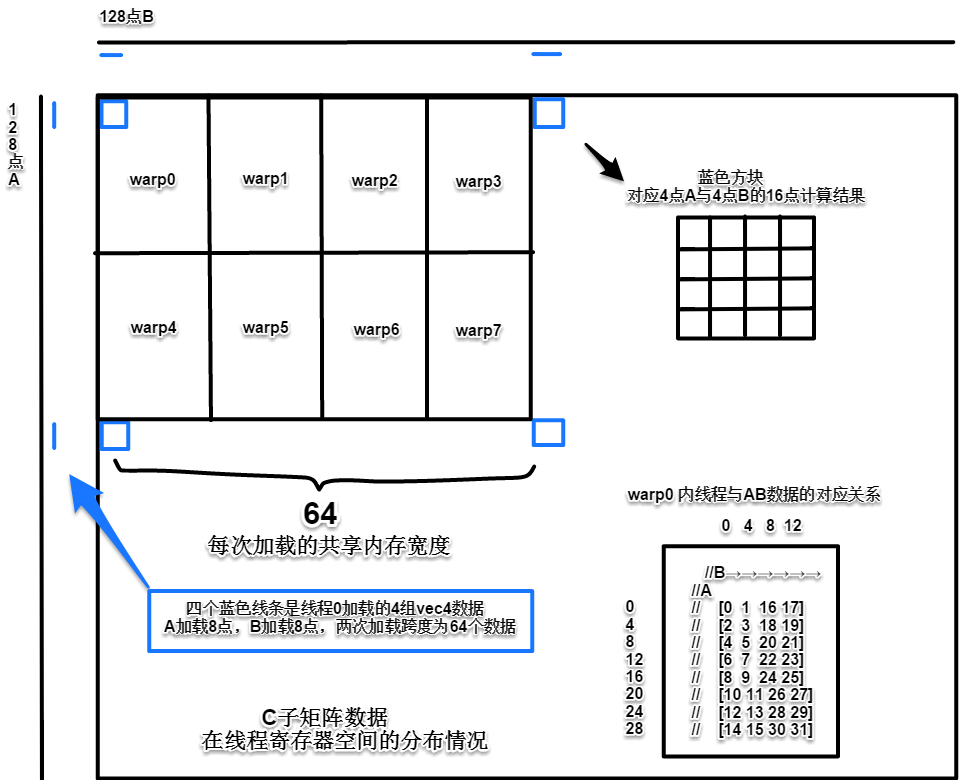
​ 矩阵A中一行（这里作者按已经转置的A矩阵描述）的每个点与矩阵B中一行的每个点一一对应。

​ 在warp内部，比较直接的方式是连续或有跨度地加载，但这样会发生不明原因的存储冲突。如果按照线程号用Z形加载就不会产生冲突（见上图warp0线程与数据关系，0、1、2、3……线程是Z字形映射）（自己没有验证过，平时只是合并访存，不知道是特定CUDA版本或架构有这个问题，还是都这样，作者没有对加载规格和模式做详尽地测试来检查哪个有效，哪个不行）。

计算C子矩阵: 寄存器组与重用

​ 现在，每个线程里都有两个寄存器组，每组8个寄存器，保存矩阵A和B的数据，通过64次FFMA乘加计算得到C子矩阵的中间结果。为了实现全速低功耗地计算，需要考虑几个问题。最基本的就是寄存器组和操作数重用。

在Maxwell架构下，寄存器组（register banks）宽度为4（即4个32bit寄存器 ）。Kepler架构（宽度也是4）直接把序号和组关联起来。而在Maxwell架构下，关联由寄存器序号对4取余得到（即每 序号%4 相同的寄存器一组，占用同一个寄存器访问端口，类似共享内存）。在Kepler架构下，可以通过调整64个FFMA指令来消除所有存储冲突。在Maxwell架构下通过操作数重用缓存（operand reuse cache）解决这一问题，同时能减少寄存器传输次数。指令的每个源操作数槽位(source operand slot)有8 bytes的数据重用缓存。每次发射指令的时候，有一个标志位用来指定对应的操作数是否将被再次引用。设置标志位后，下一条指令在同一个操作数槽位引用同一个寄存器时，不需要再到寄存器组去取这个数据。可以利用这个特性，来避免寄存器冲突。

寄存器组概念参考下图：

第一步是通过操作数重用来减少寄存器存储冲突。为实现目的，需要显式地选择要占用的寄存器。这是用MaxAs做汇编器的一个重要优点，ptxas在避免寄存器冲突方面做得还行，但不够完美，向量化存储操作做得不够好（在SGEMM实现中这点很重要）。实现如下：

  • 0-63作为矩阵C的寄存器
  • 64-71和80-87作为矩阵A的双缓冲寄存器块
  • 72-79和88-95作为矩阵B的双缓冲寄存器块

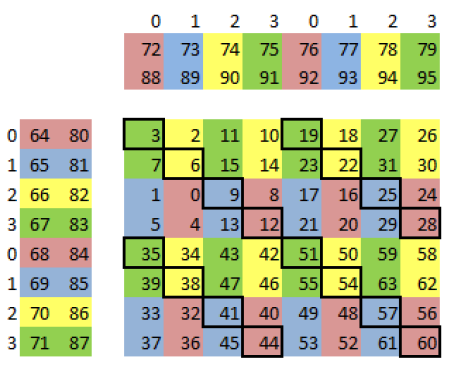
按照下图来安排8*8矩阵的寄存器，用不同的颜色表示每个寄存器所在的组位。矩阵C中，选择颜色与对应的A、B不同的寄存器（不在同一端口）。通过这种方式可以消除C中所有的寄存器冲突。但还剩下A、B的16个寄存器冲突，这些冲突位置用黑框示意（作者图）：

如果不重用缓存，16个冲突每个都有1个时钟的延迟，理论上使得计算效率下降20%左右(在518时钟的循环上再加128个时钟)。实测时，执行没有重用标记的SGEMM汇编代码，发现性能只下降了200 Gflops左右。Nvidia的operand collectors相关专利里的存储冲突（bank conflict）章节中描述了缓和存储冲突的一系列办法。不好说Maxwell架构是怎么处理的，可能利用了线程级并行（TLP）来掩盖存储冲突延迟。operand collectors能在一定程度上掩盖了存储冲突，但在大量冲突下可能不堪重负。持续地缓存能让硬件更好地避免存储冲突导致的延迟。MaxAs项目通过汇编器控制重用标记，预先判断哪些寄存器值得缓存，哪些寄存器在使用后就可以丢弃。

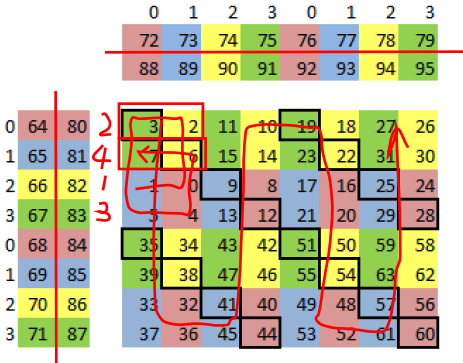
优化重用标记的工作已经由MaxAs实现了。我们要做的就是规划指令顺序，尽可能多地重用。最简单的排序是两个嵌套for循环一行一行地遍历矩阵，但这样只能用到8 bytes操作数缓存中的4 bytes，不能完全避免存储冲突。 通过往复遍历数据，可以避免所有的冲突并提高寄存器的重用率（39%）。不过作者最高效的实现方法是旋转遍历（重用率47%）。下面是FFMA指令按照矩阵C寄存器序号的执行顺序：

1, 0, 2, 3, 5, 4, 6, 7, 33, 32, 34, 35, 37, 36, 38, 39,
45, 44, 46, 47, 41, 40, 42, 43, 13, 12, 14, 15, 9, 8, 10, 11,
17, 16, 18, 19, 21, 20, 22, 23, 49, 48, 50, 51, 53, 52, 54, 55,
61, 60, 62, 63, 57, 56, 58, 59, 29, 28, 30, 31, 25, 24, 26, 27

自己做的标记如下：

通过旋转，使得C寄存器组交错加载，避免冲突。此外，向量化数据加载除了高效，还可以减少访存指令数量，从而减少存储冲突的概率。

指令访问寄存器时可能发生存储冲突，导致延迟，所以应该为操作数选则不同组的寄存器。MaxAs可以控制寄存器的映射，SGEMM代码中为track0-3, tex, readAs, readBs和writeS选择了合适的寄存器组。作者提到在cublas中（当时的版本是CUDA 6.5），第一个FFMA指令选择的寄存器有存储冲突，这里冲突不能通过重用缓存避免，因为之前没有指令加载，也就没有寄存器值能放到操作数缓存。在GM204上，这个”bug”降低了cublas 28 Gflops的性能。

最后一个有关FFMA指令的的问题是，如何交错地执行FFMA和上述提到的存储操作。具体可以对照源码sgemm_pre_64.sass来看。为了掩盖延迟，共享内存的双缓冲加载越早越好，所以和第一个FFMA指令一起双发射执行。用两条FFMA指令隔开两条加载指令，因为存储单元好像在一半吞吐率的时候工作得最优（※不要连续发射存储指令※）

1
01:-:-:-:0      FFMA cx02y00, j0Ax02, j0By00, cx02y00; // Wait Dep 1--:-:-:-:1      LDS.U.128 j1Ax00, [readAs + 4x<1*64 + 00>];--:-:-:-:1      FFMA cx02y01, j0Ax02, j0By01, cx02y01;--:-:-:-:0      FFMA cx00y01, j0Ax00, j0By01, cx00y01;--:-:-:-:1      LDS.U.128 j1By00, [readBs + 4x<1*64 + 00>];

为了不让存储单元被指令淹没（overwhelm，没译准），纹理加载在两组共享内存加载中间执行，给纹理加载指令读取操作数的机会（in flight概念）。为下一个大循环加载的数据共享内存加载指令放在最后一个FFMA指令块中。之前还有一个加在第7和第8个FFMA指令块之间的BAR.SYNC指令（同步，作用是保证整个block tex加载的数据都通过STS保存到另一共享内存buffer后，再继续下一次加载计算）。

以上所有指令执行位置是经过大量测试取最优的，这样细粒度的指令位置控制在ptxas是中无法实现的。而且ptxas有优化掉共享内存双缓冲加载方法的倾向。在选择寄存器组、优化指令执行顺序以实现操作数重用和选择存储指令位置以后，之前只能跑到硬件计算能力70%的kernel现在可以跑到98%。

理论性能的计算，用主循环中的FFMA指令总数（518）除以所有指令需要的发射时间（双发射不算）即可得到。以下是256线程版本的具体分析：

Op Count
FFMA 512
LDS 32 dual issued
STS 2 dual issued
TLD 2 dual issued
IADD 2
XOR 3
STEP 1
BAR 1 dual issued
BAR 1 dual issued

一共用了518个时钟来发送指令（双发射不计入时钟消耗），所以这个kernel的性能上限是512/518，即98.8%。大型矩阵计算的实际性能接近理论值。

根据主循环代码和指令的时钟消耗，可以粗略估计这个kernel的访存带宽上限。对于GM204架构，有：

  • 每个线程加载2组vec4的4byte数据（即32bytes）
  • 每个loop需要518个clock（之后的计算部分有具体细节）
  • 每个SM同一时刻时有128个线程执行
  • 有13个时钟频率1.2GHz的SM
  • 每GB相当于0.931GiB

所以，对于GTX 970 有：
（这里可以和上一大节的分析对比，两种分析基本能对应上，充分利用了硬件算力）

线程数据交换与写回

再次用图：

在循环的末尾（end=N-8，标记判断），线程块中的C子矩阵数据已经计算完成，要把结果存回显存。由于从共享内存进行4点向量化加载，在写回全局内存的时候，对应的矩阵C的地址并没有作合并访存优化。虽然可以直接写回，但还有优化的余地。线程间通过共享内存交换矩阵C寄存器的数据，重新组织数据，构造合并访存的写入操作。注意，这里warp shuffle指令并不适用，因为需要在不同的线程之间交换不同寄存器的数据。

如下图示意，把要交换的数据分为8块，在存放C子矩阵的寄存器中按顺序沿纵向划分。这里还是以0号线程数据为例，红色线条是第1次处理的8个数据，注意相邻线程同一次加载的B方向数据，跨度为4（两蓝色线条示意）。

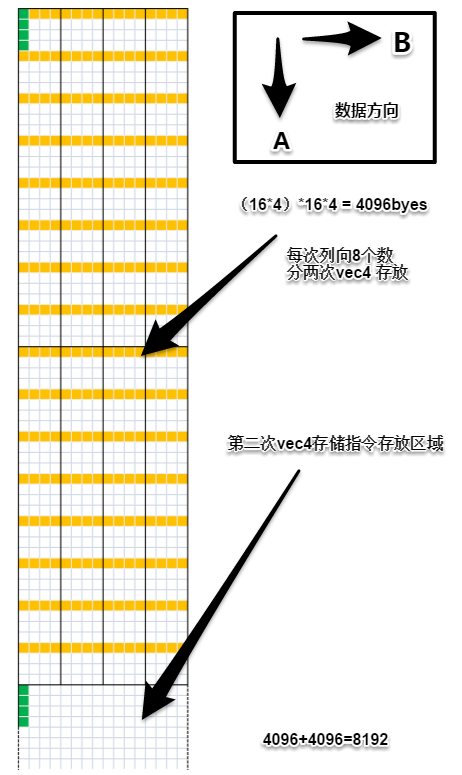
每个线程每次从8个寄存器读取数据到共享内存，借用作者配图表示：
此时的数据是按A方向存储的。绿色格子是0号线程的两组vec4数据。

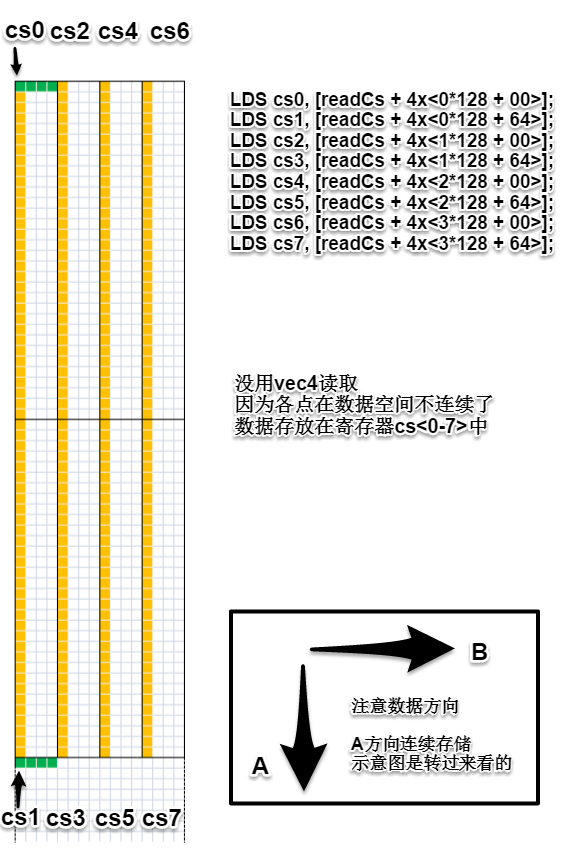
然后马上读回数据，此时按B方向读取，由于数据不连续了，分成8次单独访问。
黄色格子是线程，绿色格子是0号线程读取的数据。

​ 这里有一个细节是，上述共享内存读写不作同步，因为数据交换是在同一warp内进行的。（猜测，存储单元按指令先后处理，前面的存储工作完成后才进行后面的读取工作）最后C子矩阵计算结果从寄存器放回显存。
​ 整体来看，256个线程分为8个warp，线程与数据空间映射关系如下：

下图是64*64数据块的传输细节。
从并行的角度，各线程在A方向连续读取，因为B方向相邻4点存在同一个线程中，而且在数据空间有一行的跨度所以（为了合并访存）不能在一次传输中连续处理。因此，每次存放到共享内存空间的一行数据在B方向上有四行跨度（图中带颜色的数据方块就是1/8次传输的前一组vec4数据）。

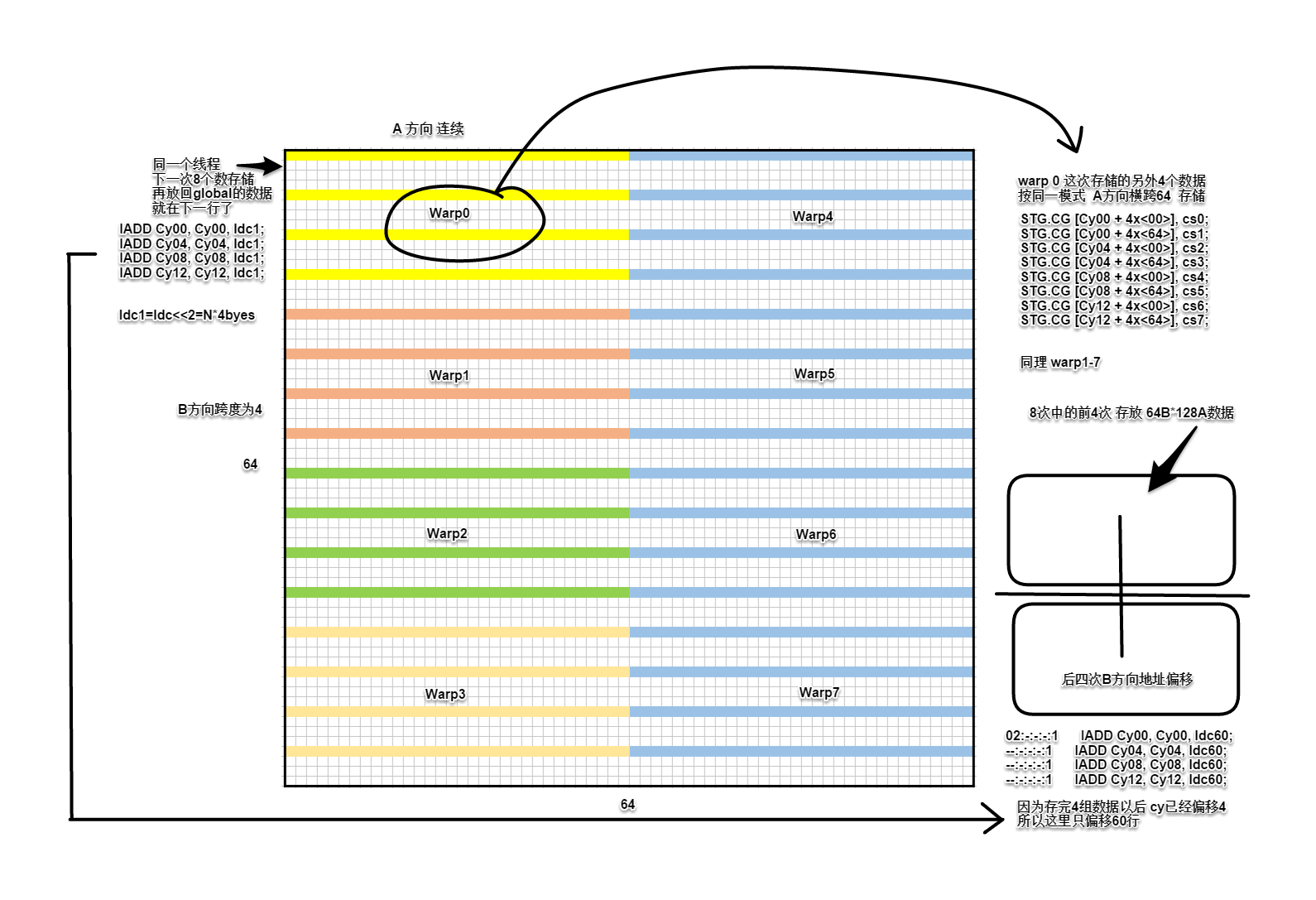
至此，就完成了一个block的计算。

赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码
载入天数...载入时分秒...

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

计算机科学先驱阿兰·图灵说，“We can only see a short distance ahead, but we can see plenty there that needs to be done.”<br> 我们只能向前看到一小段未来，但我们可以在那里看到足够多可以做的事。很难说当代一个受过良好教育的人，一个理解银河系、理解宇宙演化史、理解现代社会法则的人和16世纪一个仍然相信地球是平的的人有什么本质的区别。看起来16世纪的你一定会比21世纪的你更愚蠢，但从未知的方面看，两者其实同等幼稚。今天宏大的宇宙观可能就是另一个版本的平坦地球，如果被25世纪的人观察的话。正因为如此，图灵的话才会有意义。正是因为所有人都没有大自然聪明，才会有文明的发展，才会有人秉持真理去挑战所谓的人类权威；正是因为问题永远都无法完善，才会有生机与希望，才会有足够多的工作可以做。 所以我想实际上图灵是在说，既然都离不开这艘飞船，那就让我们在这里做一些可以做的事吧，或许会有些惊喜也说不定呢。