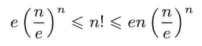《Combinatorial Optimization Theory and Algorithms(6th,2018)》是一本内容相当广泛而全面的教材,但因其证明的晦涩使人望而却步,本文的目的是整理本学期所学内容涉及的相关结果,仅给出概括性描述,如对相关结果感兴趣,可从此书中找到相关内容及引文。
多项式时间算法:算法运行时间为
$$
O(n^k)
$$强多项式时间算法:此问题的运行时间不因输入的数字大小而变动,而是依照输入数据的结构复杂度
给定图的极小连通支撑子图是支撑树,我们的目标是找一个最小(权)的树
钻孔问题:在完全图中寻找一条含有所有顶点的最短路(最短的Hamiltonian path)。
最小树形图(带有方向的树)问题:在有向图中找一个带有方向的最小支撑树。
求解最小支撑树问题的“贪婪算法”:
Kruskal算法(多项式时间算法):O(mn) → O(mlogn) → O(mα(m,n))(几乎是线性的)
Idea:从一个空图开始,每次增加原图中权最小的边,同时要避开长出圈。
- Prim算法(多项式时间算法):O(n2)→O(m+nlogn)(结合Fibonacci堆)→O(mlogβ(n,m))
Idea: 任选一个顶点作为初始集,每次不断选取初始集同剩余集间的最小权边,最终将一个点的初始集长成V(G)。
(Cheriton, Tarjan 1976) 平面图的最小支撑树问题能线性时间被求解。
平面上n个点的最小支撑树问题能在O(nlogn)时间内被求解。
(Karger,Klein,Tarjan 1976)寻找最小支撑树的一个随机算法有线性期望的运行时间。
最小树形图(带有方向的树)问题等价于最大权分支问题:
Edmonds分支算法 O(mn) →O(m+nlogn)(Gabow等1986 用Fibonacci得到)
寻求有向图G中边不交支撑树形图(根节点r)的最大集的多项式时间算法:目前最有效算法由Gabow(1995)给出。
处理更困难的组合最优化问题最常见的子问题:最小支撑树+最短路。
非负边权的最短路问题:
如果所有权值为1,则最短路问题可直接由BFS求解;
对权值都为正整数,可将边e替换成长度为c(e)的路,然后再运用BFS(可能增加指数多条边,很笨!);
更为高明的构思是Dijkstra(1959)算法(已知最好的强多项式时间算法): O(n2)→ O(m+nlogn)(Fredman,Tarjan, 1987 使用Fibonacci堆);
假设权是固定范围内的整数(0到C之间的整数),Dial(1969)用一个编号为0,…,|V(G)|·C的数组,按照当前的l值去储存顶点,从而得到简单的线性时间算法;
对平面有向图,Henzinger等(1997)给出了线性时间算法;
对非负整数权的无向图,Thorup(1999)找到了线性时间算法。(在无向图中寻找最短路极其困难)
一般守恒权(每条边权不需要非负,只要求不存在总权为负的圈(负圈)就好了)
Moore-Bellman-Ford算法(迄今最快的强多项式时间算法):O(nm)
边权为整数且有下界cmin时,Goldberg(1995)的缩放尺度法具有运行时间O(√nmlog|cmin|+2)
平面图,Fakcharoenphol和Rao(2006)阐述了一个O(nlog3n)算法。
若G含有负圈,则至今未有多项式时间算法(问题变为NP-hard)
对给定一个有向图G,权c:E(G)→R,可在O(nm)时间找到一个可行势,或找到负圈。
全点对最短路问题(找一个有向图的所有顶点有序对(s,t)求出最短的s-t路):
调用n次Moore-Bellman-Ford算法,每次选定一个s:O(n2m)→O(mn+n2logn)(P**ettie 2004**,目前已知最好的时间界);
对于非负权的稠密图,Chan(2007)得到界O(n3log3logn/log2n);
对于所有边权都是较小的正整数,Zwick(2002)运用快速矩阵乘积可以改进Pettie的时间界。
Floyd-Warshall**算法**:O(n3)
在具有守恒权的无向图G中,求全部点对之间的最短路问题可以在O(n4)时间内解决。Gabow(1983)将运行时间改进到O(min{n3,nmlogn})
在一个具有守恒权的有向图中,我们用上述最短路算法容易求出最小总权的圈。
如何求平均权为最小的圈?最小平均圈问题。
Karp(1978)**最小平均圈算法**:O(nm) 注:对任意边权的无向图,此算法不能用来求最小平均权的圈。
最大流问题
Ford-Fulkerson(1957**)最大流算法**:整值容量,指数次增流,存在整值的最大流,所以算法一定在有限步结束。
Idea:找可扩路,再沿可扩路增流
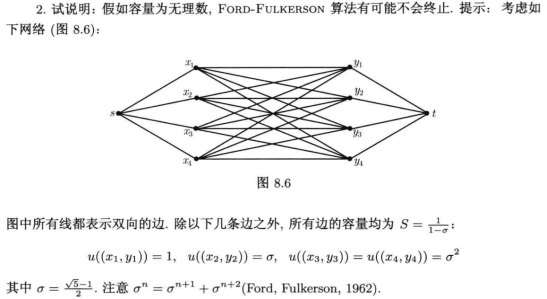
注:如果允许容量取无理数,在选择可扩路时运气不好,算法可能不会终止。
- Edmonds-Karp(1972)算法(最大流问题的第一个多项式时间算法)O(m2n)(至多有mn/2次增流,每次增流运用BFS的时间是O(m))
Idea. 把任选一条可扩路修改为找一条最短的可扩路。
- 分层图容易由BFS在O(m)时间构造出来。
- Dinic算法(多项式时间算法):至多进行n-1个阶段,每个阶段O(nm)→O(n2)
Sleator, Tarjan(1983)用一种称为动态树的数据结构使得Dinic算法成为最大流问题的O(mnlogn)算法
Fujishige(2003)算法(弱多项式时间算法,简单,缩放尺度技术):对简单有向图G及整容量可在O(mnlogumax)时间内正确求解最大流问题。
Goldberg,Tarjan(1988)**推流-重标算法:O(n2√m)→O(nmlog(n2/m))(Goldberg,Tarjan 1988)→O(nmlog2+m/(nlogn)n)(King, Rao, Tarjan 1994**)
一个具有n个顶点及m条边的最小费用流问题的实例可以变换为等价的Hitchcock运输问题的实例,其中有n+m个顶点及2m条边。
求解最小费用流的最小平均圈消去算法(强多项式时间算法):O(m3n2logn)
Idea. 首先用最大流算法求出一个b-流,然后逐次沿负权的可扩圈增流,直到没有这样的圈为止,为得到多项式的运行时间,每次选择一个平均权最小的圈是有必要的。
- 容量缩放算法(最小费用流问题的第一个多项式时间算法):O(n(m+nlogn)logbmax)
- Orlin算法(已知最快捷的强多项式时间算法):只能处理无容量限制问题 O(nlogm(m+nlogn))
原始的网络单纯形法不是多项式时间算法,但它在实用上是十分有效的。Orlin(1997)提出一种变形,可在多项式时间运行。多项式时间的对偶网路单纯形法由Orlin, Plotkin与Tardos(1993)以及Armstrong与Jim(1997)得到。
Ford与Fulkerson(1958):动态最大流(每条边上的流量可以随时间变化,而进入一条边的流要在规定的延迟时间之后才能到达另一端)问题可以用同最小费用流问题一样的运行时间求解。
- Hoppe与Tardos(2000)运用子模函数最小化解决了最速转运问题,其中有多源多汇且有整数传输时间。
- Klinz, Woeginger(2004)证明了求最小费用动态流是NP-hard的。
附录:一些有价值的结论
关于阶乘的一个不等式
按照边的权重排边可以使用合并整序算法,时间复杂度O(mlogm)。
判定一个至多有n条边的图中的圈能在O(n)内完成(用DFS\BFS来完成。
满足
$$
|E(G)|>\binom{|V(G)|-1}{2}
$$
的任一无向图G是连通的。
就像格罗滕迪克所说:“构成一个研究者创造力和想象力的本质,是他们聆听事情内部声音的能力。”这里没有等级高下,没有阶层之分,在对未知的探索前人人平等,每个人都拥有绝对的自由。