目标:
图像特征点
意义
- 单幅图像提取特征点
- 多幅图像匹配特征点
对极几何
原理
- 对极几何约束→恢复图像间摄像机三维运动
PNP
问题描述
- 三维结构,图像摄像机三维运动
ICP
问题描述
- 点云匹配关系→摄像机三维运动
三角化→二维图像上对应点的三维结构
特征点法
1 | 视觉SLAM划分 |
视觉前端(视觉里程计VO)
特征点法的前端(主流)
- 不提特征的直接法前端
- 目的:相邻图像信息→粗略相机运动
- 实现方法(按照是否需要提取特征)
优化后端
1 | 特征点法特点 |
- 运行稳定,对光照、动态物体不敏感
- 主流方法
特征点
1 | 特征点提出 |
VO根据图像估计相机运动,图像为矩阵(估计变得困难),故从图像中选取比较有代表性的点,相机视角发生少量变化后保持不变;在这些点基础上,讨论相机位姿估计问题,以及这些点的定位问题
- 经典SLAM→路标
- 视觉SLAM→图像特征(Features)
1 | 特征及特征点要求 |
特征:图像信息的另一种数字表达形式
特征点要求
- 相机运动之后保持稳定→灰度值变化范围大,故不选择
- 特别的地方→角点、边缘、区块
特征点组成
关键点(Key-Point)
该特征点在图像里的位置
描述子(Descriptor)
通常为向量,描述关键点周围像素信息
- 设计原则:外观相似的特征应有相似描述子
1 | 更稳定的局部图像特征 |
举例
SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)
充分考虑光照、尺度、旋转→计算量大
SURF
ORB(Oriented FAST and Rotated BRIEF)
改进FAST检测子不具有方向性的问题
- 采用速度极快的二进制描述子BRIEF→特征提取加速
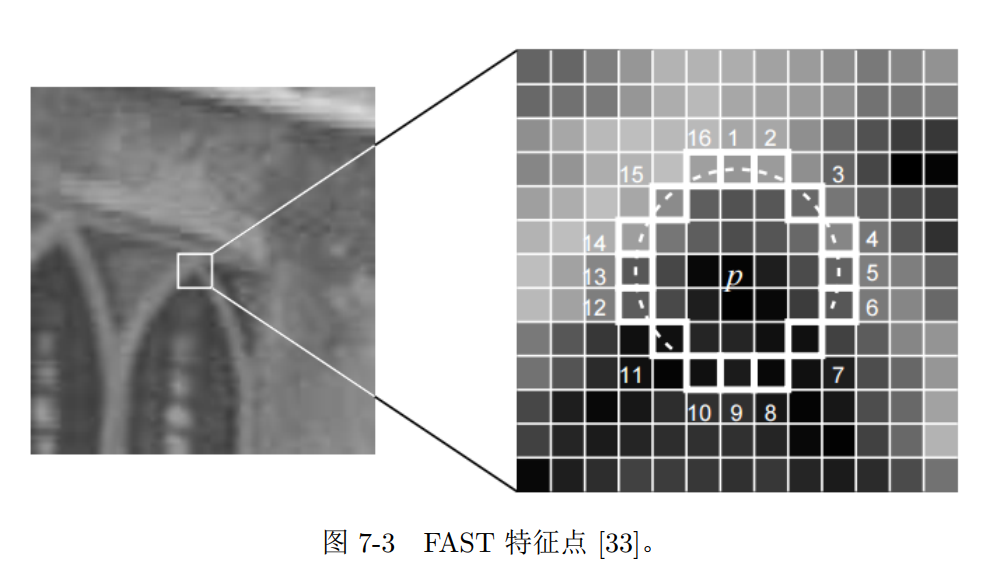
FAST关键点
计算特别快的一种特征点
- 没有描述子
性质
ORB特征
1 | 组成 |
关键点+描述子(Oriented FAST+BRIEF)
1 | 提取步骤 |
FAST角点提取
- 找出图像中的角点
- 相较原版FAST,计算特征点主方向→为BRIEF描述子增加旋转不变特性
BRIEF描述子
- 对前一步提出特征点的周围图像区域描述
1 | FAST关键点 |
思想:如果一个像素与它邻域像素差别较大,则更可能是角点(只比较像素亮度大小)特征点法
1 | 视觉SLAM划分 |
视觉前端(视觉里程计VO)
特征点法的前端(主流)
- 不提特征的直接法前端
- 目的:相邻图像信息→粗略相机运动
- 实现方法(按照是否需要提取特征)
优化后端
1 | 特征点法特点 |
- 运行稳定,对光照、动态物体不敏感
- 主流方法
特征点
1 | 特征点提出 |
VO根据图像估计相机运动,图像为矩阵(估计变得困难),故从图像中选取比较有代表性的点,相机视角发生少量变化后保持不变;在这些点基础上,讨论相机位姿估计问题,以及这些点的定位问题
- 经典SLAM→路标
- 视觉SLAM→图像特征(Features)
1 | 特征及特征点要求 |
特征:图像信息的另一种数字表达形式
特征点要求
- 相机运动之后保持稳定→灰度值变化范围大,故不选择
- 特别的地方→角点、边缘、区块
特征点组成
关键点(Key-Point)
该特征点在图像里的位置
描述子(Descriptor)
通常为向量,描述关键点周围像素信息
- 设计原则:外观相似的特征应有相似描述子
1 | 更稳定的局部图像特征 |
举例
SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)
充分考虑光照、尺度、旋转→计算量大
SURF
ORB(Oriented FAST and Rotated BRIEF)
改进FAST检测子不具有方向性的问题
- 采用速度极快的二进制描述子BRIEF→特征提取加速
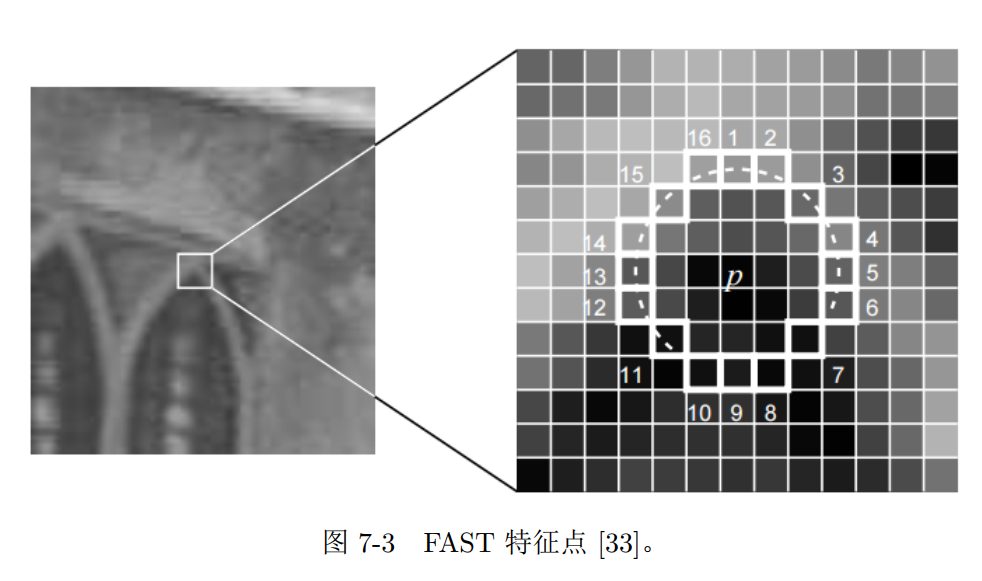
FAST关键点
计算特别快的一种特征点
- 没有描述子
性质
ORB特征
1 | 组成 |
关键点+描述子(Oriented FAST+BRIEF)
1 | 提取步骤 |
FAST角点提取
找出图像中的角点
- 相较原版FAST,计算特征点主方向→为BRIEF描述子增加旋转不变特性
BRIEF描述子
对前一步提出特征点的周围图像区域描述
1 | FAST关键点 |
思想:如果一个像素与它邻域像素差别较大,则更可能是角点(只比较像素亮度大小)特征点法
1 | 视觉SLAM划分 |
视觉前端(视觉里程计VO)
特征点法的前端(主流)
- 不提特征的直接法前端
- 目的:相邻图像信息→粗略相机运动
- 实现方法(按照是否需要提取特征)
优化后端
1 | 特征点法特点 |
- 运行稳定,对光照、动态物体不敏感
- 主流方法
特征点
1 | 特征点提出 |
VO根据图像估计相机运动,图像为矩阵(估计变得困难),故从图像中选取比较有代表性的点,相机视角发生少量变化后保持不变;在这些点基础上,讨论相机位姿估计问题,以及这些点的定位问题
- 经典SLAM→路标
- 视觉SLAM→图像特征(Features)
1 | 特征及特征点要求 |
特征:图像信息的另一种数字表达形式
特征点要求
- 相机运动之后保持稳定→灰度值变化范围大,故不选择
- 特别的地方→角点、边缘、区块
特征点组成
关键点(Key-Point)
该特征点在图像里的位置
描述子(Descriptor)
通常为向量,描述关键点周围像素信息
- 设计原则:外观相似的特征应有相似描述子
1 | 更稳定的局部图像特征 |
举例
SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)
充分考虑光照、尺度、旋转→计算量大
SURF
ORB(Oriented FAST and Rotated BRIEF)
改进FAST检测子不具有方向性的问题
- 采用速度极快的二进制描述子BRIEF→特征提取加速
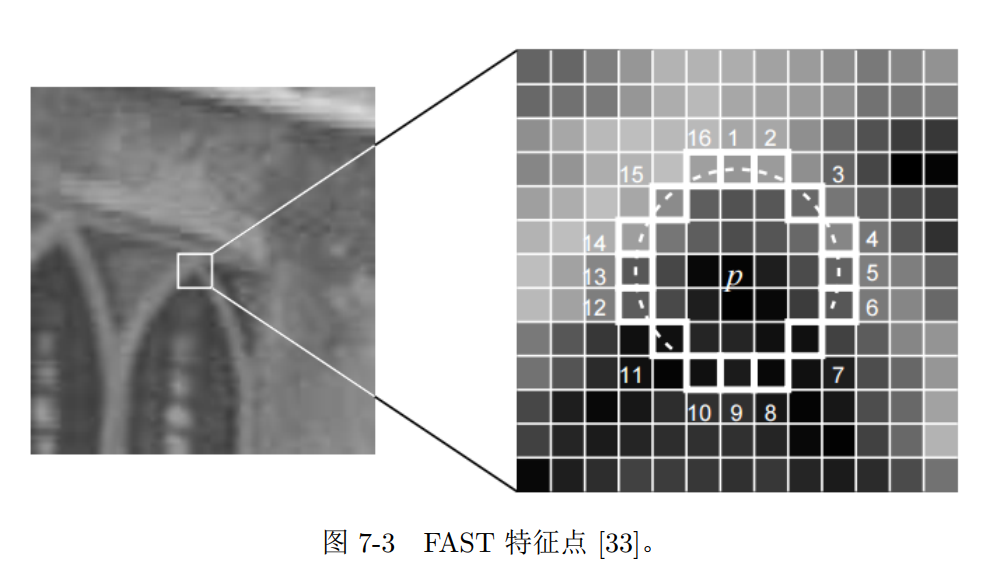
FAST关键点
计算特别快的一种特征点
- 没有描述子
性质
ORB特征
1 | 组成 |
关键点+描述子(Oriented FAST+BRIEF)
1 | 提取步骤 |
FAST角点提取
找出图像中的角点
- 相较原版FAST,计算特征点主方向→为BRIEF描述子增加旋转不变特性
BRIEF描述子
对前一步提出特征点的周围图像区域描述
1 | FAST关键点 |
思想:如果一个像素与它邻域像素差别较大,则更可能是角点(只比较像素亮度大小)
检测过程:
- 图像中选取像素 $p$, 亮度为 $I_{p}$
- 设置阈值 $T$ (如 $I_{p}$ 的 $20 \%$ )
- 以 $p$ 为中心, 选取半径为 3 的圆上16个像素点
- FAST-N, 即选取圆上, 有连续的 $\mathrm{N}$ 个点亮度 $>I_{p}+T$ or $<I_{p}-T$
- 循环执行以上四步
快速排查
- 对每个像素, 直接检测邻域圆上第1、5、9、13个像素的亮度, 只有当这四个像素中有三 个同时 $>I_{p}+T$ or $<I_{p}-T$ 时, 当前像素才有可能是一个角点
非极大值抑制(Non-Maximal Suppression) - 一定区域内仅保留响应极大值的角点, 避免角点集中
问题
| FAST角点问题 | ORB改进方法 |
|---|---|
| 特征点数量大且不确定 | 原始FAST角点计算Harris响应值,选取前N个 |
| 角点不具有方向信息 | 增加尺度描述,构建图像金字塔,且在每一层检测角点 |
| 固定取半径为3的圆,存在尺度问题 | 增加旋转描述,灰度质心法(Intensity Centroid) |
质心(以图像块灰度值作为权重的中心)
- 在一个小的图像块 $B$ 中, 定义图像块的矩为:
$$
m_{p q}=\sum_{x, y \in B} x^{p} y^{q} I(x, y), \quad p, q={0,1}
$$ - 通过矩可以找到图像块的质心:
$$
C=\left(\frac{m_{10}}{m_{00}}, \frac{m_{01}}{m_{00}}\right)
$$ - 连接图像块的几何中心 $O$ 与质心 $C$, 得到一个方向向量 $\overrightarrow{O C}$, 于是特征点的方向可 以定义为:
$$
\theta=\arctan \left(m_{01} / m_{10}\right)
$$
1 | BRIEF描述子 |
本质
- 二进制描述子,描述向量由许多个0和1组成,0和1编码了关键点附近两个像素(比如说p和q)的大小关系
的选择
- 按照某种概率分布,随机挑选
优点
| 操作 | 优点 |
|---|---|
| 随机选点 | 速度快 |
| 二进制表达 | 存储方便 |
| 关键点方向提取 | 旋转不变性实现 |
特仼匹䀨
解决问题
- SLAM中数据关联问题(Data Association), 即确定当前看到的路标与之前看到的路标之间的对应关系
存在问题 - 图像特征局部特性 $\rightarrow$ 误匹配
- 大量重复纹理 $\rightarrow$ 特征描述相似
暴力匹配(Brute-Force Matcher)
问题提出 - 图像 $I_{t}$ 中提取到特征点 $x_{t}^{m}, m=1,2, \ldots, M$, 图像 $I_{t+1}$ 中提取到特征点 $x_{t+1}^{n}, n=1,2, \ldots, N$, 如何寻找两个集合元素对应关系?
解决方法 - 对每一个特征点 $x_{t}^{m}$ 与所有的 $x_{t+1}^{n}$ 测量描述子的距离, 而后排序, 取最近为匹配点
- 改进:取不同的距离度量范数
- 浮点型描述子 $\rightarrow$ 欧氏距离
- 二进制描述子 $\rightarrow$ 汉明距离 (不同位数的个数)特仼匹䀨
解决问题- SLAM中数据关联问题(Data Association), 即确定当前看到的路标与之前看到的路标之间的对应关系
存在问题 - 图像特征局部特性 $\rightarrow$ 误匹配
- 大量重复纹理 $\rightarrow$ 特征描述相似
暴力匹配(Brute-Force Matcher)
问题提出 - 图像 $I_{t}$ 中提取到特征点 $x_{t}^{m}, m=1,2, \ldots, M$, 图像 $I_{t+1}$ 中提取到特征点 $x_{t+1}^{n}, n=1,2, \ldots, N$, 如何寻找两个集合元素对应关系?
解决方法 - 对每一个特征点 $x_{t}^{m}$ 与所有的 $x_{t+1}^{n}$ 测量描述子的距离, 而后排序, 取最近为匹配点
- 改进:取不同的距离度量范数
- 浮点型描述子 $\rightarrow$ 欧氏距离
- 二进制描述子 $\rightarrow$ 汉明距离 (不同位数的个数)
- SLAM中数据关联问题(Data Association), 即确定当前看到的路标与之前看到的路标之间的对应关系
快速近似最近邻(Q])
- 集成于OpenCV
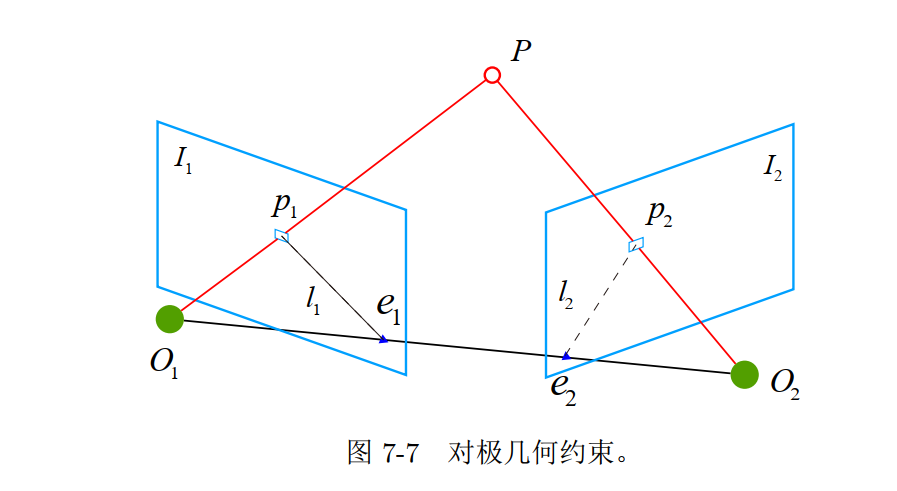
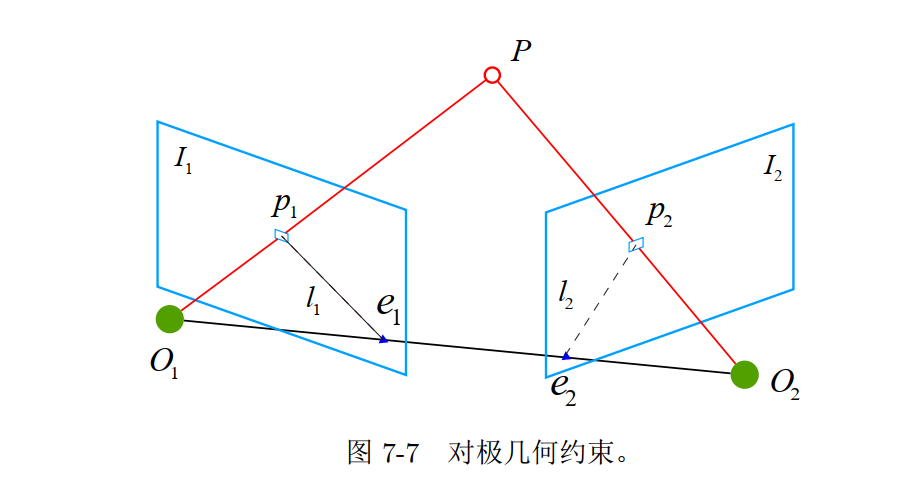
2D-2D:对极几何
对极约束
问题
- 根据若干对配对好的匹配点的对应关系 $\rightarrow$ 两帧之间摄像机运动
匹配点几何关系直观
基本输入 - $R, t \rightarrow$ 第一帧到第二帧的运动
- $O_{1}, O_{2} \rightarrow$ 相机中心
- $I_{1}, I_{2} \rightarrow$ 两帧图像
- $p_{1}, p_{2} \rightarrow$ 两帧图像中的特征点
基本概念 - 极平面(Epipolar Plane) $\rightarrow \mathrm{\Sigma O} \mathrm{O}{1} \mathrm{O}{2} \mathrm{P}$
- 极点(Epipoles) $\rightarrow e_{1}, e_{2}$
- 基线(Baseline) $\rightarrow O_{1} O_{2}$
- 极线(Epipolar Line) $\rightarrow l_{1}, l_{2}$
直观解释
匹配点代数角度
结论:
- $\boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}{1}=0$
- $\boldsymbol{p}{2}^{T} \boldsymbol{K}^{-T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{K}^{-1} \boldsymbol{p}{1}=0$
$$
\boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R}, \quad \boldsymbol{F}=\boldsymbol{K}^{-T} \boldsymbol{E} \boldsymbol{K}^{-1}, \quad \boldsymbol{x}{2}^{T} \boldsymbol{E} \boldsymbol{x}{1}=\boldsymbol{p}{2}^{T} \boldsymbol{F} \boldsymbol{p}{1}=0
$$
对极约束简洁给出两个匹配点空间位置关系,则相机位姿估计问题如下步骤
- 根据配对点像素位置, 求出 $\boldsymbol{E}$ 或 $\boldsymbol{F}$
- 根据 $E$ 或 $F$, 求出 $R, t$
注意: $E$ 与 $F$ 之间相差了相机内参, 而内参又通常已知
注意:E与F之间相差了相机内参,而内参又通常已知
推导:
第一帧坐标系下,P空间位置为
$$
\boldsymbol{P}=[X, Y, Z]^{\mathrm{T}}
$$
两个像素点 $p_{1}, p_{2}$ 的像素位置:
$$
s_{1} p_{1}=\boldsymbol{K} \boldsymbol{P}, \quad s_{2} \boldsymbol{p}{2}=\boldsymbol{K}(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t})
$$
$K$ 为相机内参矩阵, $R, t$ 为两个坐标系的相机运动, 可写为斉次坐标形式:
$$
p{1}=\boldsymbol{K} \boldsymbol{P}, \quad \boldsymbol{p}{2}=\boldsymbol{K}(\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t})
$$
取:
$$
\boldsymbol{x}{1}=\boldsymbol{K}^{-1} \boldsymbol{p}{1}, \quad \boldsymbol{x}{2}=\boldsymbol{K}^{-1} \boldsymbol{p}{2}
$$
$x{1}, x_{2}$ 是两个像素点的归一化平面上的坐标。代入上式得:
$$
x_{2}=R x_{1}+t .
$$
两边同时左乘 $t^{\wedge}$ (两侧同时与 $t$ 做外积)
$$
\boldsymbol{t}^{\wedge} \boldsymbol{x}{2}=\boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}{1}
$$
然后, 两侧同时左乘 $\boldsymbol{x}{2}^{T}$ :
$$
\boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{x}{2}=\boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}{1} .
$$
观察等式左侧, $t^{\wedge} x{2}$ 是一个与 $t$ 和 $x_{2}$ 都垂直的向量。把它再和 $x_{2}$ 做内积时,将得 到 0 。因此, 我们就得 到了一个简洁的式子:
$$
\boldsymbol{x}{2}^{T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{x}{1}=0 .
$$
重新代入 $\boldsymbol{p}{1}, \boldsymbol{p}{2}$ ,有:
$$
\boldsymbol{p}{2}^{T} \boldsymbol{K}^{-T} \boldsymbol{t}^{\wedge} \boldsymbol{R} \boldsymbol{K}^{-1} \boldsymbol{p}{1}=0 .
$$
这两个式子都称为对极约束, 它以形式简洁著名。它的几何意义是 $O_{1}, P, O_{2}$ 三者共 面。对极约束中同时包 含了平移和旋转。我们把中间部分记作两个矩阵: 基础矩阵 (Fundamental Matrix) $\boldsymbol{F}$ 和本质矩阵 (Essential Matrix) $E$ ,可以进一步简化对极约束:
$$
\boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R}, \quad \boldsymbol{F}=\boldsymbol{K}^{-T} \boldsymbol{E} \boldsymbol{K}^{-1}, \quad \boldsymbol{x}{2}^{T} \boldsymbol{E} \boldsymbol{x}{1}=\boldsymbol{p}{2}^{T} \boldsymbol{F} \boldsymbol{p}{1}=0
$$
本质矩阵
基本信息
$\boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R}$, 为 $3 \times 3$ 矩阵, 9个末知数
注意
- $\boldsymbol{E}$ 在不同尺度下等价
- 由对极约束(等式为零的约束) $\rightarrow E$ 乘以任意非零常数后,对极约束仍然满足
- 本质矩阵的内在性质
- $\boldsymbol{E}=\boldsymbol{t}^{\wedge} \boldsymbol{R} \rightarrow \boldsymbol{E}$ 的奇异值必定是 $[\sigma, \sigma, 0]^{T}$ 的形式
- 自由度
- 平移+旋转 $\stackrel{\text { 尺度等价性 }}{\longrightarrow} 5$ 个自由度
八点法估计本质矩阵
结论:
推导:
一对匹配点的归一化坐标为: $x_{1}=\left[u_{1}, v_{1}, 1\right]^{T}, x_{2}=\left[u_{2}, v_{2}, 1\right]^{T}$
根据对极约束, 有:
$$
\left(u_{1}, v_{1}, 1\right)\left(\begin{array}{lll}
e_{1} & e_{2} & e_{3} \
e_{4} & e_{5} & e_{6} \
e_{7} & e_{8} & e_{9}
\end{array}\right)\left(\begin{array}{c}
u_{2} \
v_{2} \
1
\end{array}\right)=0
$$
矩阵 $E$ 展开, 写成向量的形式:
$$
e=\left[e_{1}, e_{2}, e_{3}, e_{4}, e_{5}, e_{6}, e_{7}, e_{8}, e_{9}\right]^{T}
$$
则对极约束可以写成与 $e$ 有关的线性形式:
$$
\left[u_{1} u_{2}, u_{1} v_{2}, u_{1}, v_{1} u_{2}, v_{1} v_{2}, v_{1}, u_{2}, v_{2}, 1\right] \cdot e=0
$$
同理, 对于其它点对也有相同的表示。我们把所有点都放到一个方程中, 变成线性方 程组 $\left(u^{i}, v^{i}\right.$ 表示 第 $i$ 个特征点, 以此类推):
$$
\left(\begin{array}{ccccccccc}
u_{1}^{1} u_{2}^{1} & u_{1}^{1} v_{2}^{1} & u_{1}^{1} & v_{1}^{1} u_{2}^{1} & v_{1}^{1} v_{2}^{1} & v_{1}^{1} & u_{2}^{1} & v_{2}^{1} & 1 \
u_{1}^{2} u_{2}^{2} & u_{1}^{2} v_{2}^{2} & u_{1}^{2} & v_{1}^{2} u_{2}^{2} & v_{1}^{2} v_{2}^{2} & v_{1}^{2} & u_{2}^{2} & v_{2}^{2} & 1 \
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \
u_{1}^{8} u_{2}^{8} & u_{1}^{8} v_{2}^{8} & u_{1}^{8} & v_{1}^{8} u_{2}^{8} & v_{1}^{8} v_{2}^{8} & v_{1}^{8} & u_{2}^{8} & v_{2}^{8} & 1
\end{array}\right)\left(\begin{array}{l}
e_{1} \
e_{2} \
e_{3} \
e_{4} \
e_{5} \
e_{6} \
e_{7} \
e_{8} \
e_{9}
\end{array}\right)=0
$$
这八个方程构成了一个线性方程组
- 系数矩阵 $\rightarrow$ 特征点位置构成, 大小为 $8 \times 9$
- $e$ 位于该矩阵的零空间中
- 系数矩阵满秩 $(8) \rightarrow$ 零空间维数为 1 , 也就是 $e$ 构成一条线
SVD方法: 由估计的本质矩阵恢复相机运动
SVD方法:根据已经估得的本质矩阵 $E$, 恢复出相机的运动 $R, t$
设 $E$ 的 SVD 分解为:
$$
\boldsymbol{E}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T}
$$
$\boldsymbol{U}, \boldsymbol{V}$ 为正交阵, $\boldsymbol{\Sigma}$ 为奇异值矩阵。由 $\boldsymbol{E}$ 内在性质知 $\boldsymbol{\Sigma}=\operatorname{diag}(\sigma, \sigma, 0)$. 在 SVD 分解中, 对于任意一 个 $E$, 存在两个可能的 $t, R$ 与它对应:
$$
\begin{aligned}
\boldsymbol{t}{1}^{\wedge} &=\boldsymbol{U} \boldsymbol{R}{Z}\left(\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, \quad \boldsymbol{R}{1}=\boldsymbol{U} \boldsymbol{R}{Z}^{T}\left(\frac{\pi}{2}\right) \boldsymbol{V}^{T} \
\boldsymbol{t}{2}^{\wedge}=\boldsymbol{U} \boldsymbol{R}{Z}\left(-\frac{\pi}{2}\right) \boldsymbol{\Sigma} \boldsymbol{U}^{T}, & \boldsymbol{R}{2}=\boldsymbol{U} \boldsymbol{R}{Z}^{T}\left(-\frac{\pi}{2}\right) \boldsymbol{V}^{T}
\end{aligned}
$$ - $R_{Z}\left(\frac{\pi}{2}\right) \rightarrow$ 沿 $Z$ 轴旋转 90 度得到的旋转矩阵
- $-\boldsymbol{E}$ 和 $E$ 等价, 所以对任意一个 $t$ 取负号, 也会得到同样的结果
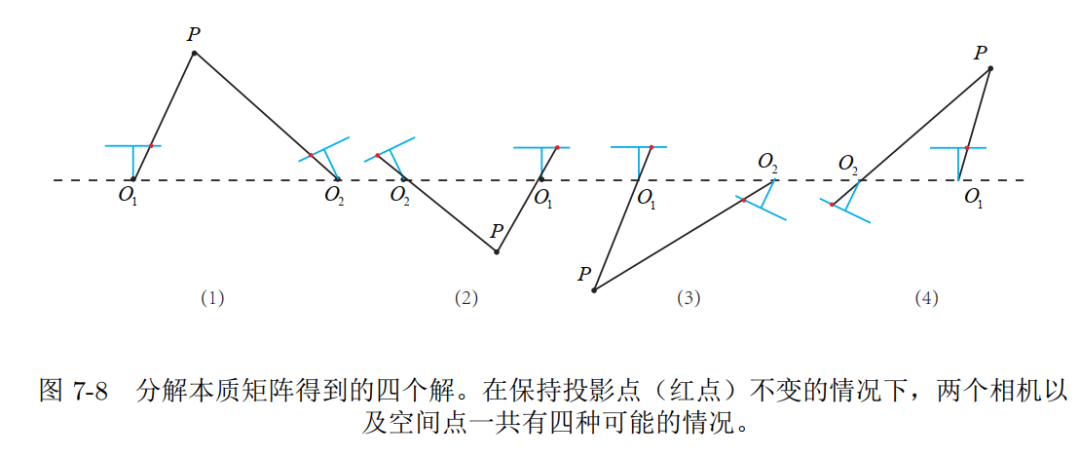
- 从 $\boldsymbol{E}$ 分解到 $t, \boldsymbol{R}$, 一共存在四个可能的解
SVD方法下的四个可能的解
- 只有第一种解, $P$ 在两个相机中都具有正的深度 $\rightarrow$ 只要把任意一点带入四种解中,检测该点在两个相 机下的深度便可确定解的正确性
- $\boldsymbol{E} \stackrel{S V D}{\longrightarrow} \boldsymbol{\Sigma}=\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right) \stackrel{\text { 取 }}{\longrightarrow} \boldsymbol{E}=\boldsymbol{U} \operatorname{diag}\left(\frac{\sigma_{1}+\sigma_{2}}{2}, \frac{\sigma_{1}+\sigma_{2}}{2}, 0\right) \boldsymbol{V}^{T}$
- 将求出的矩阵投影到 $E$ 所在流形上
单应矩阵
描述信息
单应矩阵 (Homography) $\boldsymbol{H}$ : 描述两个平面之间的映射关系
应用场景
若场景中的特征点都落在同一平面上 (比如墙, 地面等), 则可以通过单应性来进行运动估计
- 无人机携带的俯视相机
- 扫地机携带的顶视相机
数学模型建立
图像 $I_{1}$ 和 $I_{2}$ 有一对匹配好的特征点 $p_{1}$ 和 $p_{2}$ 。这些特征点落在某平面上。平面满足方程:
$$
\boldsymbol{n}^{T} \boldsymbol{P}+d=0 .
$$
稍加整理,得:
$$
-\frac{\boldsymbol{n}^{T} \boldsymbol{P}}{d}=1
$$
然后, 回顾本开头的式得:
$$
\begin{aligned}
p_{2} &=K(R P+t) \
&=K\left(R P+t \cdot\left(-\frac{n^{T} P}{d}\right)\right) \
&=K\left(R-\frac{t n^{T}}{d}\right) P \
&=K\left(R-\frac{t n^{T}}{d}\right) K^{-1} p_{1}
\end{aligned}
$$
得到了一个直接描述图像坐标 $p_{1}$ 和 $p_{2}$ 之间的变换, 把中间这部分记为 $\boldsymbol{H}$, 于是
$$
\boldsymbol{p}{2}=\boldsymbol{H} \boldsymbol{p}{1}
$$
其定义与旋转、平移以及平面的参数有关
求解思路–直接线性变换法(Direct Linear Transform)
整体思路: - 将 $H$ 矩阵看成向量, 通过解该向量的线性方程来恢复 $H$
数学推导:
与基础矩阵 $F$ 类似, 单应矩阵 $H$ 也是一个 $3 \times 3$ 的矩阵, 求解时的思路也和 $F$ 类似, 同样地可以先根据匹 配点计算 $H$, 然后 将它分解以计算旋转和平移。把上式展开,得:
$$
\left(\begin{array}{c}
u_{2} \
v_{2} \
1
\end{array}\right)=\left(\begin{array}{lll}
h_{1} & h_{2} & h_{3} \
h_{4} & h_{5} & h_{6} \
h_{7} & h_{8} & h_{9}
\end{array}\right)\left(\begin{array}{c}
u_{1} \
v_{1} \
1
\end{array}\right)
$$
请注意这里的等号是在非零因子下成立的。我们在实际处理中,通常乘以一个非零因子使得 $h_{9}=1$ (在它取 非零值时)。然后根据第三行, 去掉这个非零因子, 于是有:
$$
\begin{aligned}
&u_{2}=\frac{h_{1} u_{1}+h_{2} v_{1}+h_{3}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \
&v_{2}=\frac{h_{4} u_{1}+h_{5} v_{1}+h_{6}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} .
\end{aligned}
$$
整理得:
$$
\begin{aligned}
&h_{1} u_{1}+h_{2} v_{1}+h_{3}-h_{7} u_{1} u_{2}-h_{8} v_{1} u_{2}=u_{2} \
&h_{4} u_{1}+h_{5} v_{1}+h_{6}-h_{7} u_{1} v_{2}-h_{8} v_{1} v_{2}=v_{2}
\end{aligned}
$$
这样一组匹配点对就可以构造出两项约束 (事实上有三个约束,但是因为线性相关,只取前两个), 于是自由度 为 8 的单应矩阵可以通过 4 对匹配特征点算出(注意: 这些特征点不能有三点共线的情况), 即求解以下的线 性方程组 (当 $h_{9}=0$ 时, 右侧为零)
$$
\left(\begin{array}{cccccccc}
u_{1}^{1} & v_{1}^{1} & 1 & 0 & 0 & 0 & -u_{1}^{1} u_{2}^{1} & -v_{1}^{1} u_{2}^{1} \
0 & 0 & 0 & u_{1}^{1} & v_{1}^{1} & 1 & -u_{1}^{1} v_{2}^{1} & -v_{1}^{1} v_{2}^{1} \
u_{1}^{2} & v_{1}^{2} & 1 & 0 & 0 & 0 & -u_{1}^{2} u_{2}^{2} & -v_{1}^{2} u_{2}^{2} \
0 & 0 & 0 & u_{1}^{2} & v_{1}^{2} & 1 & -u_{1}^{2} v_{2}^{2} & -v_{1}^{2} v_{2}^{2} \
u_{1}^{3} & v_{1}^{3} & 1 & 0 & 0 & 0 & -u_{1}^{3} u_{2}^{3} & -v_{1}^{3} u_{2}^{3} \
0 & 0 & 0 & u_{1}^{3} & v_{1}^{3} & 1 & -u_{1}^{3} v_{2}^{3} & -v_{1}^{3} v_{2}^{3} \
u_{1}^{4} & v_{1}^{4} & 1 & 0 & 0 & 0 & -u_{1}^{4} u_{2}^{4} & -v_{1}^{4} u_{2}^{4} \
0 & 0 & 0 & u_{1}^{4} & v_{1}^{4} & 1 & -u_{1}^{4} v_{2}^{4} & -v_{1}^{4} v_{2}^{4}
\end{array}\right)\left(\begin{array}{c}
h_{1} \
h_{2} \
h_{3} \
h_{4} \
h_{5} \
h_{6} \
h_{7} \
h_{8}
\end{array}\right)=\left(\begin{array}{c}
u_{2}^{1} \
v_{2}^{1} \
u_{2}^{2} \
v_{2}^{2} \
u_{2}^{3} \
v_{2}^{3} \
u_{2}^{4} \
v_{2}^{4}
\end{array}\right)
$$
单应矩阵到相机运动
单应矩阵 $\stackrel{\text { 分解 }}{\longrightarrow} \boldsymbol{R}, \boldsymbol{t}$ : - 数值法
- 解析法
单应性意义 - 为了避免退化现象造成的影响,同时估计基础矩阵 $\boldsymbol{F}$ 和单应矩阵 $\boldsymbol{H}$, 选择重投影误差比较小的那个 作为最终的运动估计矩阵
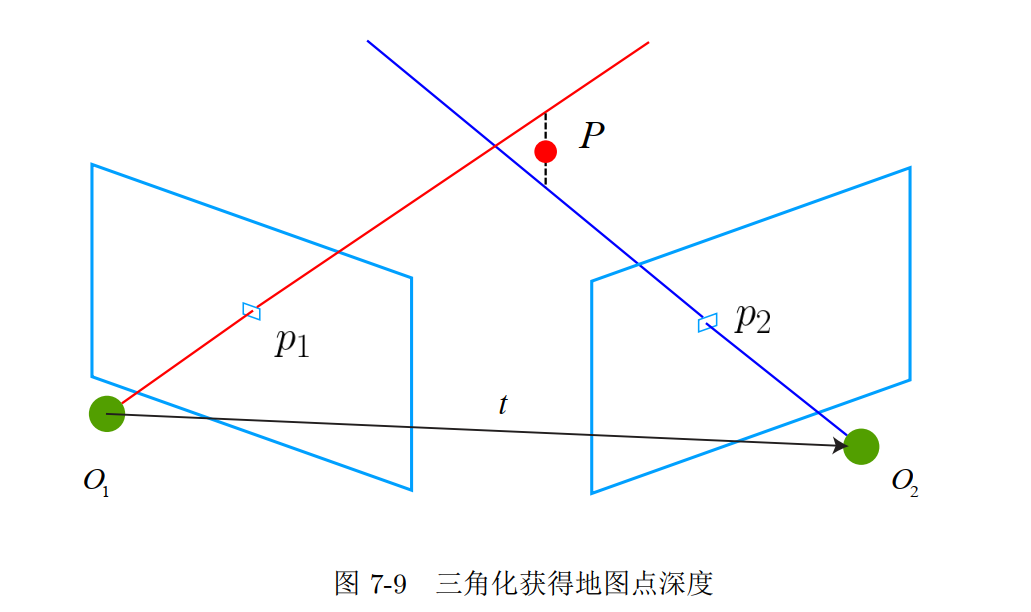
三角测量
三角测量定义
- 通过在两处观察同一个点的夹角,确定该点的距离
三角测量数学描述
输入元素:
- 图像 $I_{1}$ 和 $I_{2}$
- 相机光心 $O_{1}$ 和 $O_{2}$
- 特征点 $p_{1}, p_{2}$
对极几何 $\boldsymbol{R}, \boldsymbol{t} \rightarrow s_{1}, s_{2}$ 设 $x_{1}, x_{2}$ 为两个特征点的归一化坐标, 那么它们满足:
$$
s_{1} \boldsymbol{x}{1}=s{2} \boldsymbol{R} \boldsymbol{x}_{2}+\boldsymbol{t}
$$ - $s_{2}$ 求解
先对上式两侧左乘一个 $\boldsymbol{x}{1}^{\wedge}$ ,得:
$$
s{1} \boldsymbol{x}{1}^{\wedge} \boldsymbol{x}{1}=0=s_{2} \boldsymbol{x}{1}^{\wedge} \boldsymbol{R} \boldsymbol{x}{2}+\boldsymbol{x}{1}^{\wedge} \boldsymbol{t} .
$$
该式左侧为零, 右侧可看|成 $s{2}$ 的一个方程, 可以根据它直接求得 $s_{2}$
3D-2D:PnP
1 | PnP用途 |
- 求解3D到2D点对运动的方法
- 已知n个3D空间点及其投影位置→相机所在位姿
1 | 应用情况 |
| 相机 | 方法 |
|---|---|
| 双目/RGB-D | 直接使用 |
| 单目视觉 | 先初始化,后使用 |
1 | 求解方法 |
三对点估计位姿
- P3P
- 直接线性变换
- EPnP
- UPnP
非线性优化
- Bundle Adjustment
直接线性变换
1 | 思路 |
直接将T矩阵看成12个未知数,
过程
- 空间点 $P$ 齐次坐标为 $P=(X, Y, Z, 1)^{T}$
- 在图像 $I_{1}$ 中投影到特征 $x_{1}=\left(u_{1}, v_{1}, 1\right)^{T}$ (归一化平面齐次坐标表示 )
- 相机的位姿 $R, t$ 末知
- 定义增广矩阵 $[R \mid t]$ 为一个 $3 \times 4$ 的矩阵(包含了旋转与平移信息)
- 展开形式列写如下
$$
s\left(\begin{array}{l}
u_{1} \
v_{1} \
1
\end{array}\right)=\left(\begin{array}{llll}
t_{1} & t_{2} & t_{3} & t_{4} \
t_{5} & t_{6} & t_{7} & t_{8} \
t_{9} & t_{10} & t_{11} & t_{12}
\end{array}\right)\left(\begin{array}{l}
X \
Y \
Z \
1
\end{array}\right)
$$ - 用最后一行把 $s$ 消去, 得到两个约束
$$
u_{1}=\frac{t_{1} X+t_{2} Y+t_{3} Z+t_{4}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}} \quad v_{1}=\frac{t_{5} X+t_{6} Y+t_{7} Z+t_{8}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}}
$$ - 为了简化表示, 定义 $T$ 的行向量
$$
t_{1}=\left(t_{1}, t_{2}, t_{3}, t_{4}\right)^{T}, t_{2}=\left(t_{5}, t_{6}, t_{7}, t_{8}\right)^{T}, t_{3}=\left(t_{9}, t_{10}, t_{11}, t_{12}\right)^{T}
$$ - 于是有
$$
\boldsymbol{t}{1}^{T} \boldsymbol{P}-\boldsymbol{t}{3}^{T} \boldsymbol{P} u_{1}=0 \boldsymbol{t}{2}^{T} \boldsymbol{P}-\boldsymbol{t}{3}^{T} \boldsymbol{P} v_{1}=0
$$
请注意 $t$ 是待求的变量, 可以看到每个特征点提供了两个关于 $t$ 的线性约束。假设一共有 $N$ 个特征 点, 可以列出线性方程组.
$$
\left(\begin{array}{ccc}
P_{1}^{T} & 0 & -u_{1} P_{1}^{T} \
0 & P_{1}^{T} & -v_{1} P_{1}^{T} \
\vdots & \vdots & \vdots \
P_{N}^{T} & 0 & -u_{N} P_{N}^{T} \
0 & P_{N}^{T} & -v_{N} P_{N}^{T}
\end{array}\right)\left(\begin{array}{c}
t_{1} \
t_{2} \
t_{3}
\end{array}\right)=0
$$
由于 $t$ 一共有 12 维, 因此最少通过六对匹配点,即可实现矩阵 $T$ 的线性求解
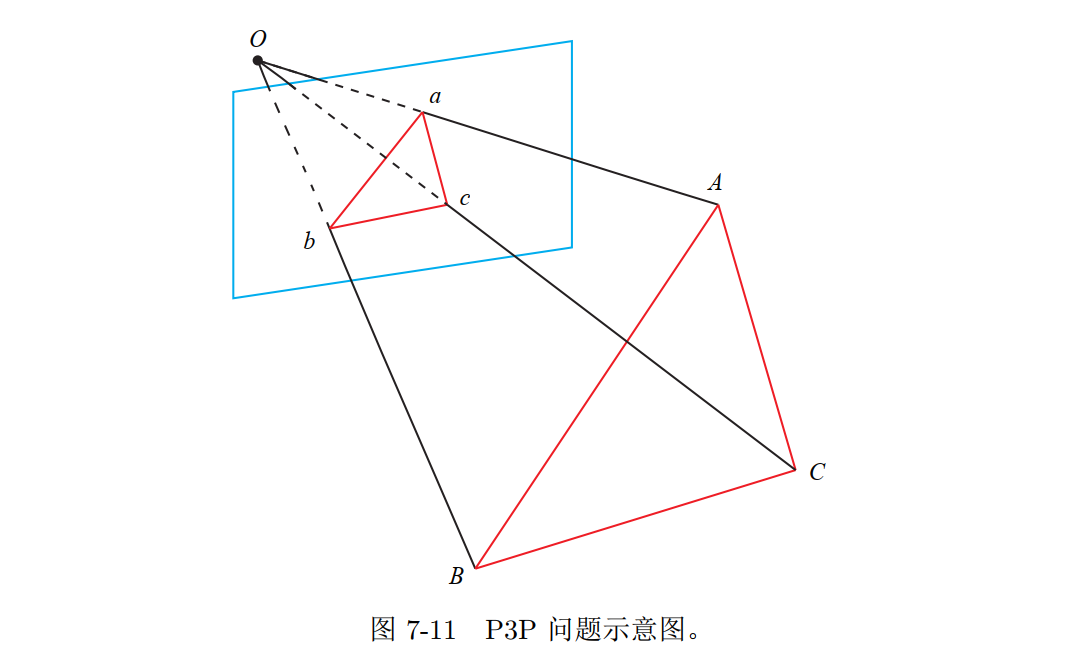
P3P
优点
- 仅使用三对匹配点, 对数据要求较少
输入数据 - 三对3D-2D匹配点
- 3D: $A, B, C$ (世界坐标系中坐标)
- 2D: $a, b, c$
- 一对验证点
- $D-d$
思想
利用了三角形相似性质,求解投影点 $a, b, c$ 在相机坐标系下的 $3 \mathrm{D}$ 坐标, 最后把问题转换成一个 3D 到 3D 的位姿估计问题(带有匹配信息的 3D-3D 位姿求解非常容易)
思路 - 三角形对应关系
$$
\Delta O a b-\Delta O A B, \quad \Delta O b c-\Delta O B C, \quad \Delta O a c-\Delta O A C .
$$ - 余弦定理
$$
O A^{2}+O B^{2}-2 O A \cdot O B \cdot \cos \langle a, b\rangle=A B^{2} O B^{2}+O C^{2}-2 O B \cdot O C \cdot \cos \langle b, c\rangle=B C^{2} O A^{2}+
$$ - 同除 $O C^{2}$, 且记 $x=O A / O C, y=O B / O C$
$$
x^{2}+y^{2}-2 x y \cos \langle a, b\rangle=A B^{2} / O C^{2} y^{2}+1^{2}-2 y \cos \langle b, c\rangle=B C^{2} / O C^{2} x^{2}+1^{2}-2 x \cos \langle a, c\rangle
$$ - 记 $v=A B^{2} / O C^{2}, u v=B C^{2} / O C^{2}, w v=A C^{2} / O C^{2}$
$$
x^{2}+y^{2}-2 x y \cos \langle a, b\rangle-v=0 y^{2}+1^{2}-2 y \cos \langle b, c\rangle-u v=0 x^{2}+1^{2}-2 x \cos \langle a, c\rangle-w v=
$$ 将(1)中 $v$ 代入 (2)、(3)优点
- 仅使用三对匹配点, 对数据要求较少
输入数据 - 三对3D-2D匹配点
- 3D: $A, B, C$ (世界坐标系中坐标)
- 2D: $a, b, c$
- 一对验证点
- $D-d$
思想
利用了三角形相似性质,求解投影点 $a, b, c$ 在相机坐标系下的 $3 \mathrm{D}$ 坐标, 最后把问题转换成一个 3D 到 3D 的位姿估计问题(带有匹配信息的 3D-3D 位姿求解非常容易)
思路 - 三角形对应关系
$$
\Delta O a b-\Delta O A B, \quad \Delta O b c-\Delta O B C, \quad \Delta O a c-\Delta O A C .
$$ - 余弦定理
$$
O A^{2}+O B^{2}-2 O A \cdot O B \cdot \cos \langle a, b\rangle=A B^{2} O B^{2}+O C^{2}-2 O B \cdot O C \cdot \cos \langle b, c\rangle=B C^{2} O A^{2}+
$$ - 同除 $O C^{2}$, 且记 $x=O A / O C, y=O B / O C$
$$
x^{2}+y^{2}-2 x y \cos \langle a, b\rangle=A B^{2} / O C^{2} y^{2}+1^{2}-2 y \cos \langle b, c\rangle=B C^{2} / O C^{2} x^{2}+1^{2}-2 x \cos \langle a, c\rangle
$$ - 记 $v=A B^{2} / O C^{2}, u v=B C^{2} / O C^{2}, w v=A C^{2} / O C^{2}$
$$
x^{2}+y^{2}-2 x y \cos \langle a, b\rangle-v=0 y^{2}+1^{2}-2 y \cos \langle b, c\rangle-u v=0 x^{2}+1^{2}-2 x \cos \langle a, c\rangle-w v=
$$ - 将(1)中 $v$ 代入 (2)、(3)
- 仅使用三对匹配点, 对数据要求较少
$$
(1-u) y^{2}-u x^{2}-\cos \langle b, c\rangle y+2 u x y \cos \langle a, b\rangle+1=0(1-w) x^{2}-w y^{2}-\cos \langle a, c\rangle x+2 w x y c
$$
:warning:关于 $x, y$ 的二元二次方程
- 已知量
- $\cos \langle a, b\rangle, \cos \langle b, c\rangle, \cos \langle a, c\rangle$
- $u=B C^{2} / A B^{2}, w=A C^{2} / A B^{2}$
- 末知量
- $x, y$
- 求解注意
- 解析法: 吴消元法[45]
- 数值法:类似于分解 $\boldsymbol{E}$, 四个解后验证
存在问题
- P3P 只利用三个点的信息。当给定的配对点多于 3 组时,难以利用更多的信息。
- 如果 3D 点或 $2 \mathrm{D}$ 点受噪声影响, 或者存在误匹配, 则算法失效
Bundle Adjustment
思想
$\mathrm{PnP} \rightarrow$ 李代数上的非线性最小二乘问题
- 线性方法
- 先求相机位姿, 再求空间点位置
- 非线性优化
- 把它们都看成优化变量, 放在一起优化
- Bundle Adjustment, 最小化重投影误差 (Reprojection error)
思路
考虑 $n$ 个三维空间点 $P$ 和它们的投影 $p$, 我们希望计算相机的位姿 $\boldsymbol{R}, \boldsymbol{t}$, 它的李代数表示为 $\xi_{0}$ 假设某 空间点坐标为 $\boldsymbol{P}{i}=\left[X{i}, Y_{i}, Z_{i}\right]^{T}$ ,其投影的像素坐标为 $\boldsymbol{u}{i}=\left[u{i}, v_{i}\right]^{T}$ 。则像素位置与空间点位置的关 系如下:
$$
s_{i}\left[\begin{array}{c}
u_{i} \
v_{i} \
1
\end{array}\right]=\boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right)\left[\begin{array}{c}
X_{i} \
Y_{i} \
Z_{i} \
1
\end{array}\right]
$$
写成矩阵形式就是
$$
s_{i} \boldsymbol{u}{i}=\boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}{i}
$$
由于相机位姿末知以及观测点的噪声, 该等式存在一个误差把误差求和, 构建最小二乘问题, 然后寻找 最好的相机位姿, 使它最小化:
$$
\boldsymbol{\xi}^{*}=\arg \min {\xi} \frac{1}{2} \sum{i=1}^{n}\left|\boldsymbol{u}{i}-\frac{1}{s{i}} \boldsymbol{K} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}{i}\right|{2}^{2}
$$
误差项:将像素坐标(观测到的投影位置)与 3D 点按照当前估计的位姿进行投影得到的位置相比较得 到的误差, 所以称之为重投影误差。
使用 $\mathrm{G}-\mathrm{N}$ 和 $\mathrm{L}-\mathrm{M}$ 之前, 我们需要知道每个误差项关于优化变量的导数, 也就是线性化:
$$
e(x+\Delta x) \approx e(x)+J \Delta x
$$
这里的 $J$ 的形式是值得讨论的,甚至可以说是关键所在。我们固然可以使用数值导 数, 但如果能够推 导解析形式时, 我们会优先考虑解析导数。现在, 当 $e$ 为像素坐标误差(2维), $x$ 为相机位姿 ( 6 维) 时, $J$ 将是一个 $2 \times 6$ 的矩阵。我们来推导 $J$ 的形式。
J的形式推导
回忆李代数的内容, 我们介绍了如何使用扰动模型来求李代数的导数。首先, 记变换 到相机坐标系下的 空间点坐标为 $\boldsymbol{P}^{\prime}$, 并且把它前三维取出来:
$$
\boldsymbol{P}^{\prime}=\left(\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}\right){1: 3}=\left[X^{\prime}, Y^{\prime}, Z^{\prime}\right]^{T}
$$
那么,相机投影模型相对于 $\boldsymbol{P}^{\prime}$ 则为:
$$
s \boldsymbol{u}=\boldsymbol{K} \boldsymbol{P}^{\prime}
$$
展开之:
$$
\left[\begin{array}{c}
s u \
s v \
s
\end{array}\right]=\left[\begin{array}{ccc}
f{x} & 0 & c_{x} \
0 & f_{y} & c_{y} \
0 & 0 & 1
\end{array}\right]\left[\begin{array}{c}
X^{\prime} \
Y^{\prime} \
Z^{\prime}
\end{array}\right]
$$
利用第 3 行消去 $s$ ( 实际上就是 $P^{\prime}$ 的距离 ),得:
$$
u=f_{x} \frac{X^{\prime}}{Z^{\prime}}+c_{x}, \quad v=f_{y} \frac{Y^{\prime}}{Z^{\prime}}+c_{y}
$$
在定义了中间变量后,我们对 $\xi^{\wedge}$ 左乘扰动量 $\delta \xi$, 然后考虑 $e$ 的变化关于 扰动量的导数。利用链式法 则, 可以列写如下:
$$
\frac{\partial e}{\partial \delta \boldsymbol{\xi}}=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{e(\delta \boldsymbol{\xi} \oplus \boldsymbol{\xi})}{\delta \boldsymbol{\xi}}=\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}^{\prime}} \frac{\partial \boldsymbol{P}^{\prime}}{\partial \delta \boldsymbol{\xi}}
$$
$$
\frac{\partial \boldsymbol{e}}{\partial \delta \boldsymbol{\xi}}=\lim {\delta \boldsymbol{\xi} \rightarrow 0} \frac{e(\delta \boldsymbol{\xi} \oplus \boldsymbol{\xi})}{\delta \boldsymbol{\xi}}=\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}^{\prime}} \frac{\partial \boldsymbol{P}^{\prime}}{\partial \delta \boldsymbol{\xi}}
$$
这里的 $\oplus$ 指李代数上的左乘扰动。第一项是误差关于投影点的导数, 在式 (7.40) 已 经列出了变量之 间的关系, 易得:
$$
\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}^{\prime}}=-\left[\begin{array}{lll}
\frac{\partial u}{\partial X^{\prime}} & \frac{\partial u}{\partial Y^{\prime}} & \frac{\partial u}{\partial Z^{\prime}} \
\frac{\partial v}{\partial X^{\prime}} & \frac{\partial v}{\partial Y^{\prime}} & \frac{\partial v}{\partial Z^{\prime}}
\end{array}\right]=-\left[\begin{array}{ccc}
\frac{f{x}}{Z^{\prime}} & 0 & -\frac{f_{x} X^{\prime}}{Z^{22}} \
0 & \frac{f_{y}}{Z^{\prime}} & -\frac{f_{y} Y^{\prime}}{Z^{\prime 2}}
\end{array}\right]
$$
而第二项为变换后的点关于李代数的导数, 根据在 $4.3 .5$ 中的推导, 得:
$$
\frac{\partial(\boldsymbol{T} \boldsymbol{P})}{\partial \delta \boldsymbol{\xi}}=(\boldsymbol{T} \boldsymbol{P})^{\odot}=\left[\begin{array}{cc}
\boldsymbol{I} & -\boldsymbol{P}^{\prime \wedge} \
\mathbf{0}^{T} & \mathbf{0}^{T}
\end{array}\right]
$$
而在 $\boldsymbol{P}^{\prime}$ 的定义中, 我们取出了前三维, 于是得:
$$
\frac{\partial \boldsymbol{P}^{\prime}}{\partial \delta \boldsymbol{\xi}}=\left[\boldsymbol{I},-\boldsymbol{P}^{\prime \wedge}\right] .
$$
将这两项相乘, 就得到了 $2 \times 6$ 的雅可比矩阵:
$$
\frac{\partial e}{\partial \delta \boldsymbol{\xi}}=-\left[\begin{array}{cccccc}
\frac{f_{x}}{Z^{\prime}} & 0 & -\frac{f_{x} X^{\prime}}{Z^{22}} & -\frac{f_{x} X^{\prime} Y^{\prime}}{Z^{\prime 2}} & f_{x}+\frac{f_{x} X^{2}}{Z^{\prime 2}} & -\frac{f_{x} Y^{\prime}}{Z^{\prime}} \
0 & \frac{f_{y}}{Z^{\prime}} & -\frac{f_{y} Y^{\prime}}{Z^{\prime 2}} & -f_{y}-\frac{f_{y} Y^{\prime 2}}{Z^{\prime 2}} & \frac{f_{y} X^{\prime} Y^{\prime}}{Z^{\prime 2}} & \frac{f_{y} X^{\prime}}{Z^{\prime}}
\end{array}\right]
$$
这个雅可比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系。我们保留了前面的负号, 因为 这是由于误差是由观测值减预测值定义的。它当然也可反过来, 定义成 预测减观测” 的形式。在那种情 况下, 只要去掉前面的负号即可。此外, 如果 $\mathfrak{s e}(3)$ 的定义方式是旋转在前, 平移在后时, 只要把这个 矩阵的前三列与后三列对调即可。另一方面, 除了优化位姿, 我们还希望优化特征点的空间位置。因 此, 需要讨论 $e$ 关于空间点 $P$ 的导数。所幸这个导数矩阵相对来说容易一些。仍利用链式法则, 有:
$$
\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}}=\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}^{\prime}} \frac{\partial \boldsymbol{P}^{\prime}}{\partial \boldsymbol{P}}
$$
第一项已在前面推导了, 第二项,按照定义
$$
\boldsymbol{P}^{\prime}=\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{P}=\boldsymbol{R} \boldsymbol{P}+\boldsymbol{t}
$$
我们发现 $\boldsymbol{P}^{\prime}$ 对 $\boldsymbol{P}$ 求导后只剩下 $\boldsymbol{R}$ 。于是
$$
\frac{\partial \boldsymbol{e}}{\partial \boldsymbol{P}}=-\left[\begin{array}{ccc}
\frac{f_{x}}{Z^{\prime}} & 0 & -\frac{f_{x} X^{\prime}}{Z^{2}} \
0 & \frac{f_{y}}{Z^{\prime}} & -\frac{f_{y} Y^{\prime}}{Z^{2}}
\end{array}\right] \boldsymbol{R}
$$
3D-3D: ICP
问题描述
一组配对好的 3D 点:
$$
\boldsymbol{P}=\left{\boldsymbol{p}{1}, \ldots, \boldsymbol{p}{n}\right}, \quad \boldsymbol{P}^{\prime}=\left{\boldsymbol{p}{1}^{\prime}, \ldots, \boldsymbol{p}{n}^{\prime}\right}
$$
要找一个欧氏变换 $R, t$, 使得:
$$
\forall i, \boldsymbol{p}{i}=\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}
$$
可用迭代最近点(Iterative Closest Point, ICP ) 求解
求解方式
- 线性代数:SVD
- 非线性优化
SVD方法
基础定义 - 定义第 $i$ 对点的误差项
$$
\boldsymbol{e}{i}=\boldsymbol{p}{i}-\left(\boldsymbol{R} \boldsymbol{p}_{i}^{\prime}+\boldsymbol{t}\right)
$$
- 构建最小二乘问题, 求使误差平方和达到极小的 $R \cdot t$
$$
\min {\boldsymbol{R}, t} J=\frac{1}{2} \sum{i=1}^{n}\left|\left(\boldsymbol{p}{i}-\left(\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}\right)\right)\right|_{2}^{2}
$$
求解方法推导 - 定义两组点的质心
$$
\boldsymbol{p}=\frac{1}{n} \sum_{i=1}^{n}\left(\boldsymbol{p}{i}\right), \quad \boldsymbol{p}^{\prime}=\frac{1}{n} \sum{i=1}^{n}\left(\boldsymbol{p}_{i}^{\prime}\right)
$$ - 在误差函数中作处理
$$
\begin{array}{r}
\frac{1}{2} \sum_{i=1}^{n}\left|\boldsymbol{p}{i}-\left(\boldsymbol{R} \boldsymbol{p}{i}^{\prime}+\boldsymbol{t}\right)\right|^{2}=\frac{1}{2} \sum_{i=1}^{n}\left|\boldsymbol{p}{i}-\boldsymbol{R} \boldsymbol{p}{i}^{\prime}-\boldsymbol{t}-\boldsymbol{p}+\boldsymbol{R} \boldsymbol{p}^{\prime}+\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}\right|^{2} \
=\frac{1}{2} \sum_{i=1}^{n}\left|\left(\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right)+\left(\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}-\boldsymbol{t}\right)\right|^{2} \
=\frac{1}{2} \sum_{i=1}^{n}\left(\left|\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right|^{2}+\left|\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}-\boldsymbol{t}\right|^{2}+\right. \
\left.2\left(\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right)^{T}\left(\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}-\boldsymbol{t}\right)\right)
\end{array}
$$ - 由 $\left(\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right)$ 在求和后为零, 优化目标函数简化为
$$
\min {R, t} J=\frac{1}{2} \sum{i=1}^{n}\left|\boldsymbol{p}{i}-\boldsymbol{p}-\boldsymbol{R}\left(\boldsymbol{p}{i}^{\prime}-\boldsymbol{p}^{\prime}\right)\right|^{2}+\left|\boldsymbol{p}-\boldsymbol{R} \boldsymbol{p}^{\prime}-\boldsymbol{t}\right|^{2}
$$ 令第二项为零就能得到 $t$
求解步骤总结
- $\boldsymbol{R}$ 的求解,展开关于 $\boldsymbol{R}$ 的误差项,得
$$
\frac{1}{2} \sum_{i=1}^{n}\left|\boldsymbol{q}{i}-\boldsymbol{R} \boldsymbol{q}{i}^{\prime}\right|^{2}=\frac{1}{2} \sum_{i=1}^{n} \boldsymbol{q}{i}^{T} \boldsymbol{q}{i}+\boldsymbol{q}{i}^{T} \boldsymbol{R}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime}-2 \boldsymbol{q}{i}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime}
$$ - 第一项和 $\boldsymbol{R}$ 无关, 第二项由于 $\boldsymbol{R}^{T} \boldsymbol{R}=\boldsymbol{I}$, 亦与 $\boldsymbol{R}$ 无关。则优化目标函数变为
$$
\sum_{i=1}^{n}-\boldsymbol{q}{i}^{T} \boldsymbol{R} \boldsymbol{q}{i}^{\prime}=\sum_{i=1}^{n}-\operatorname{tr}\left(\boldsymbol{R} \boldsymbol{q}{i}^{\prime} \boldsymbol{q}{i}^{T}\right)=-\operatorname{tr}\left(\boldsymbol{R} \sum_{i=1}^{n} \boldsymbol{q}{i}^{\prime} \boldsymbol{q}{i}^{T}\right)
$$ - 定义矩阵
$$
\boldsymbol{W}=\sum_{i=1}^{n} \boldsymbol{q}{\boldsymbol{i}} \boldsymbol{q}{i}^{T}
$$ - 对 $W$ 进行 SVD 分解
$$
\boldsymbol{W}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T}
$$
其中, $\Sigma$ 为奇异值组成的对角矩阵, 对角线元素从大到小排列,而 $U$ 和 $V$ 为正交矩 阵。当 $W$ 满秩 时, $\boldsymbol{R}$ 为:
$$
\boldsymbol{R}=\boldsymbol{U} \boldsymbol{V}^{T}
$$
解得 $\boldsymbol{R}$ 后求解 $\boldsymbol{t}$ 即可
非线性优化方法
以迭代的方式去找最优值。以李代数表达位姿时, 目标函数可以写成:
$$
\min {\boldsymbol{\xi}}=\frac{1}{2} \sum{i=1}^{n}\left|\left(\boldsymbol{p}{i}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}{i}^{\prime}\right)\right|{2}^{2}
$$
单个误差项关于位姿导数已经在前面推导过了, 使用李代数扰动模型即可:
$$
\frac{\partial \boldsymbol{e}}{\partial \delta \boldsymbol{\xi}}=-\left(\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}{i}^{\prime}\right)^{\odot}
$$
非线性优化中只需不断迭代, 我们就能找到极小值 - ICP问题唯一解
- 只要我们能找到极小值解, 那么这个极小值就是全局最优值
- ICP问题无穷多解
基于特征点的视觉里程计的几个重要问题
- 特征点是如何提取并匹配的
- 如何通过 $2 \mathrm{D}-2 \mathrm{D}$ 的特征点估计相机运动
- 如何从 $2 \mathrm{D}-2 \mathrm{D}$ 的匹配估计一个点的空间位置
- 3D-2D 的 PnP 问题, 它的线性解法和 Bundle Adjustment 解法
- 3D-3D 的 ICP 问题, 其线性解法和 Bundle Adjustment 解法