目标:
- 针孔相机模型、内参、径向畸变参数
- 一个空间点如何投影到相机成像平面
- OpenCV图像存储与表达方式
- 摄像头标定方法
引子
观测方程部分机器人如何观测外部世界(视觉SLAM中指相机成像过程)
相机模型投影关系的描述、相机内参
双目成像、RGB-D相机原理二维照片像素基本操作点云拼接
相机模型
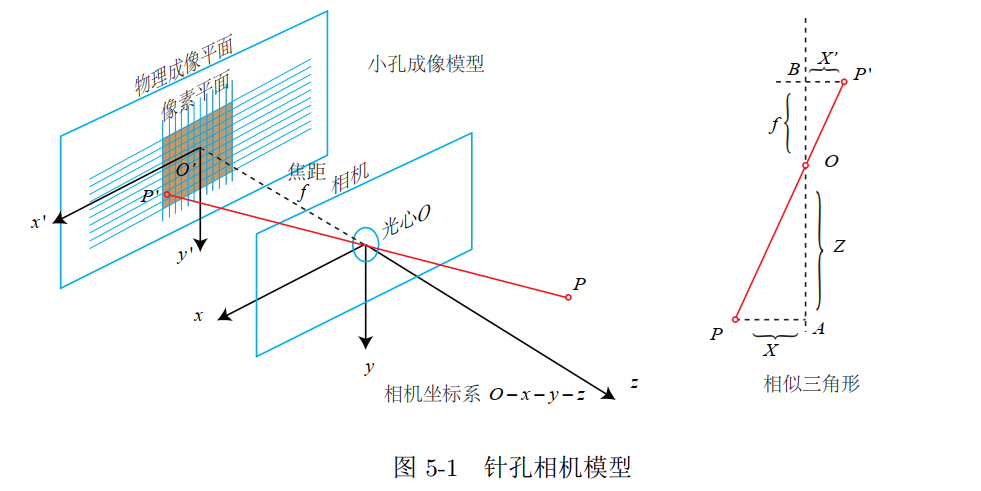
针孔相机模型
光线通过针孔之后,在针孔背面投影成像的关系
1 | 点P与它的像之间的空间关系 |
$\frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}}$
负号表示:成像倒立;简化模型:
$$
\frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}}
$$
$$
\begin{aligned}
&X^{\prime}=f \frac{X}{Z} \
&Y^{\prime}=f \frac{Y}{Z}
\end{aligned}
$$
内参数矩阵
猫述传感器将感受到的光线转换成图像像素的过程
$P^{\prime}$ 坐标与像素坐标关系:
$$
\left{\begin{array}{l}
u=\alpha X^{\prime}+c_{x} \
v=\beta Y^{\prime}+c_{y}
\end{array}\right.
$$
$$
\begin{aligned}
&X^{\prime}=f \frac{X}{Z} \
&Y^{\prime}=f \frac{Y}{Z}
\end{aligned}
$$
$$
\left{\begin{array}{l}
u=f_{x} \frac{X}{Z}+c_{x} \
v=f_{y} \frac{Y}{Z}+c_{y}
\end{array}\right.
$$
变为齐次坐标及矩阵表示:
$$
\left(\begin{array}{l}
u \
v \
1
\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}
f_{x} & 0 & c_{x} \
0 & f_{y} & c_{y} \
0 & 0 & 1
\end{array}\right)\left(\begin{array}{l}
X \
Y \
Z
\end{array}\right) \triangleq \frac{1}{Z} \boldsymbol{K} \boldsymbol{P}
$$
把Z挪到左侧:
$$
Z\left(\begin{array}{l}
u \
v \
1
\end{array}\right)=\left(\begin{array}{ccc}
f_{x} & 0 & c_{x} \
0 & f_{y} & c_{y} \
0 & 0 & 1
\end{array}\right)\left(\begin{array}{l}
X \
Y \
Z
\end{array}\right) \triangleq \boldsymbol{K} \boldsymbol{P}
$$
$K$ 内参数矩阵 $\rightarrow$ 相机出厂后固定
外参数矩阵
$P$ 的相机坐标, 应该是其世界坐标 $\left(P_{w}\right)$ 根据相机当前位姿变换到相机坐标系下的结 果, 即:
$$
Z \boldsymbol{P}{u v}=Z\left[\begin{array}{l}
u \
v \
1
\end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R} \boldsymbol{P}{w}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_{w}
$$
注意:
- 后一个式子隐含了一次齐次坐标到非齐次坐标的转换 $\rightarrow P$ 的世界坐标到像素坐标的 投影关系
- 相机的位姿 $\boldsymbol{R}, \boldsymbol{t}$ 又称为相机的外参数 (Camera Extrinsics)
- 外参会随着相机运动发生改变, 同时也是 SLAM中待估计的目标, 代表着机器人 的轨迹。
因为齐次坐标乘上非零常数后表达同样的含义, 所以可以简单地把 $Z$ 去掉:
$$
\boldsymbol{P}{u v}=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}{w}
$$
但这样等号意义就变了, 成为在齐次坐标下相等的概念, 相差了一个非零常数。为了 避免 麻烦, 我们还是从传统意义下来定义书写等号。 - $\boldsymbol{T} \boldsymbol{P}{w}$ 表示把一个世界坐标系下的齐次坐标, 变换到相机坐标系下
$P$ 在相机归一化平面上的投影:
$$
\tilde{\boldsymbol{P}}{c}=\left[\begin{array}{l}
X \
Y \
Z
\end{array}\right]=\left(\boldsymbol{T} \boldsymbol{P}{w}\right){(1: 3)}, \quad \boldsymbol{P}_{c}=\left[\begin{array}{l}
X / Z \
Y / Z \
1
\end{array}\right]
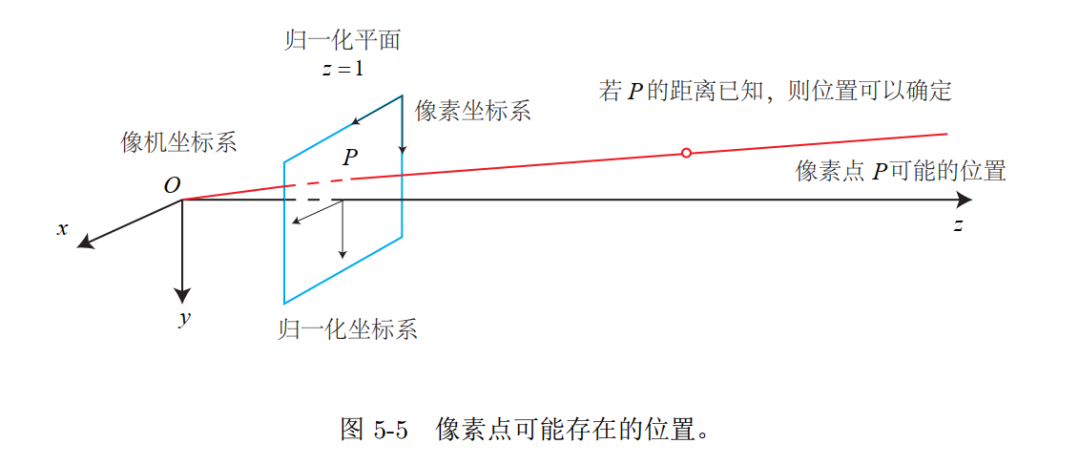
$$ - $P_{c}$ 可以看成一个二维的齐次坐标, 称为归一化坐标 (位于相机前方 $z=1$ 处 的平 面上。该平面称为归一化平面)
- 由于 $\boldsymbol{P}_{c}$ 经过内参之后就得到了像素坐标, 所以我们 可以把像素坐标 $[u, v]^{T}$ ,看成 对归一化平面上的点进行量化测量的结果
畸变
相机镜头上透镜的存在,使得光线投影到成像平面过程中产生畸变
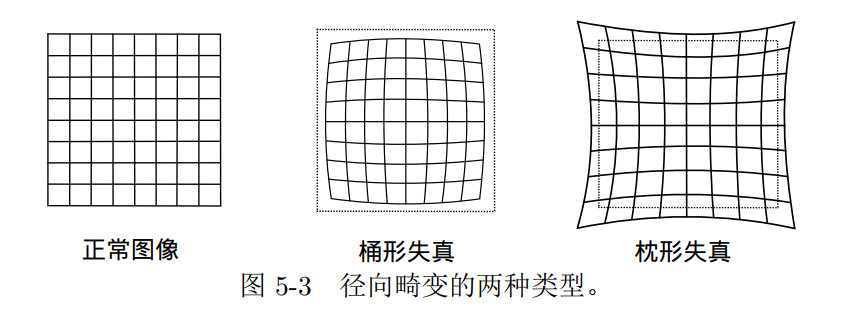
1 | 畸变类型 |
| 畸变类型 | 原因 | 描述 | 二级分类 |
|---|---|---|---|
| 径向畸变 | 透镜形状引起 | 坐标点沿着长度方向发生变化 | 桶形畸变 |
| 枕形畸变 | |||
| 切向畸变 | 透镜与成像面不严格平行 | 坐标点沿着切线方向发生变化 |
纠正方法
- 径向畸变 $x_{\text {corrected }}=x\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)$
$y_{\text {corrected }}=y\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)$ - 切向畸变 $x_{\text {corrected }}=x+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right)$
$[x, y]^{T}$ : 末纠正的点的坐标, $\left[x_{\text {corrected }}, y_{\text {corrected }}\right]^{T}$ 是纠正后的点的坐标 (归一化平面上的点而非像素平面上的点)
-中心区域: $k_{1}$ 起作用 - 边缘区域: $k_{2}$ 起作用
- 畸变很大 (鱼眼镜头……):加入 $k_{3}$ 畸变项对畸变进行纠正
纠正流程
相机坐标系中的一点 $P(X, Y, Z)$, 通过五个畸变系数找到这个点在像素平面上的正确 位置:
- 将三维空间点投影到归一化图像平面。设它的归一化坐标为 $[x, y]^{T}$ 。
- 对归一化平面上的点进行径向畸变和切向畸变纠正。
$$
\left{\begin{array}{l}
x_{\text {corrected }}=x\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right) \
y_{\text {corrected }}=y\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y
\end{array}\right.
$$ - 将纠正后的点通过内参数矩阵投影到像素平面, 得到该点在图像上的正确位置。
$$
\left{\begin{array}{l}
u=f_{x} x_{\text {corrected }}+c_{x} \
v=f_{y} y_{\text {corrected }}+c_{y}
\end{array} .\right.
$$
畸变校正两方法
- 先对整张图像去畸变 $\rightarrow$ 讨论此图像上点的空间位置 (更常见)
- 考虑图像中某个点 $\rightarrow$ 按照去畸变方程讨论其去畸变后的空间位置
1 | 畸变校正两方法 |
- 先对整张图像去畸变→讨论此图像上点的空间位置(更常见)
- 考虑图像中某个点→按照去畸变方程讨论其去畸变后的空间位置
小结
- 世界坐标系下固定点 $P$ ,界坐标为 $P_{w}$
- $P$ 的相机坐标: $\tilde{\boldsymbol{P}}{c}=\boldsymbol{R} \boldsymbol{P}{\boldsymbol{w}}+\boldsymbol{t}$
- $\tilde{\boldsymbol{P}}$ 的 $X, Y, Z \equiv$ 个量投影到归一化平面 $Z=1$ 上,归一化相机坐标 $\boldsymbol{P}_{c}=[X / Z, Y / Z, 1]^{T}$
- 归一化坐标经过内参, 对应到像素坐标 $P_{u v}=K P_{c}$
双目相机模型
1 | 空间点位置的确定 |
当P的深度确定时,我们才能确切知道它的空间位置
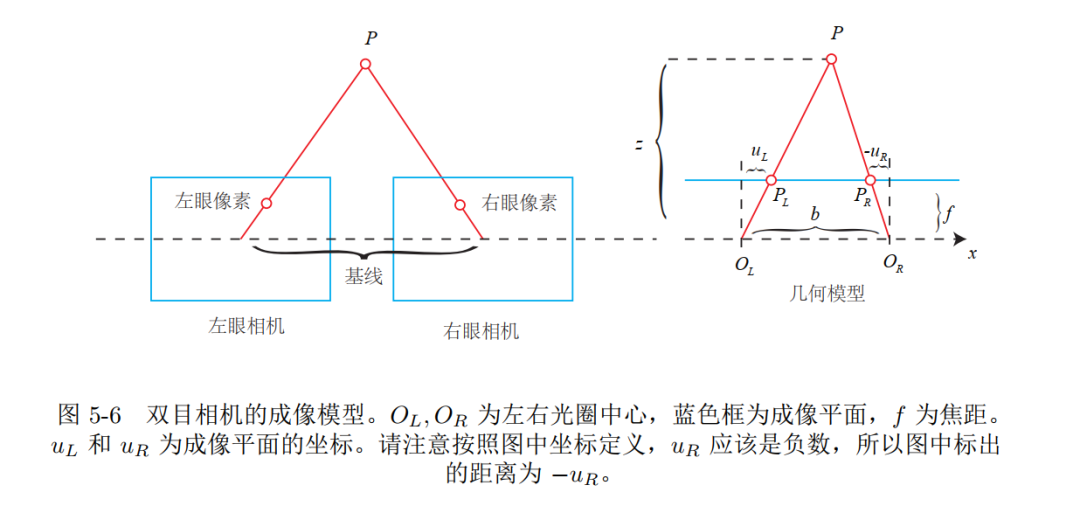
1 | 双目相机成像模型 |
空间点左右眼成像分别为 $P_{L}, P_{R}, \mathrm{x}$ 轴上位移对应到 $\mathrm{u}$ 轴上的 $u_{L}, u_{R}$, 由 $\Delta P P_{L} P_{R} \sim \Delta P O_{L} O_{R}$
整理后得到
$$
\frac{z-f}{z}=\frac{b-u_{L}+u_{R}}{b}
$$
$$
z=\frac{f b}{d}, \quad d=u_{L}-u_{R}
$$
- $d$ 为左右图的横坐标之差,称为视差 (Disparity)
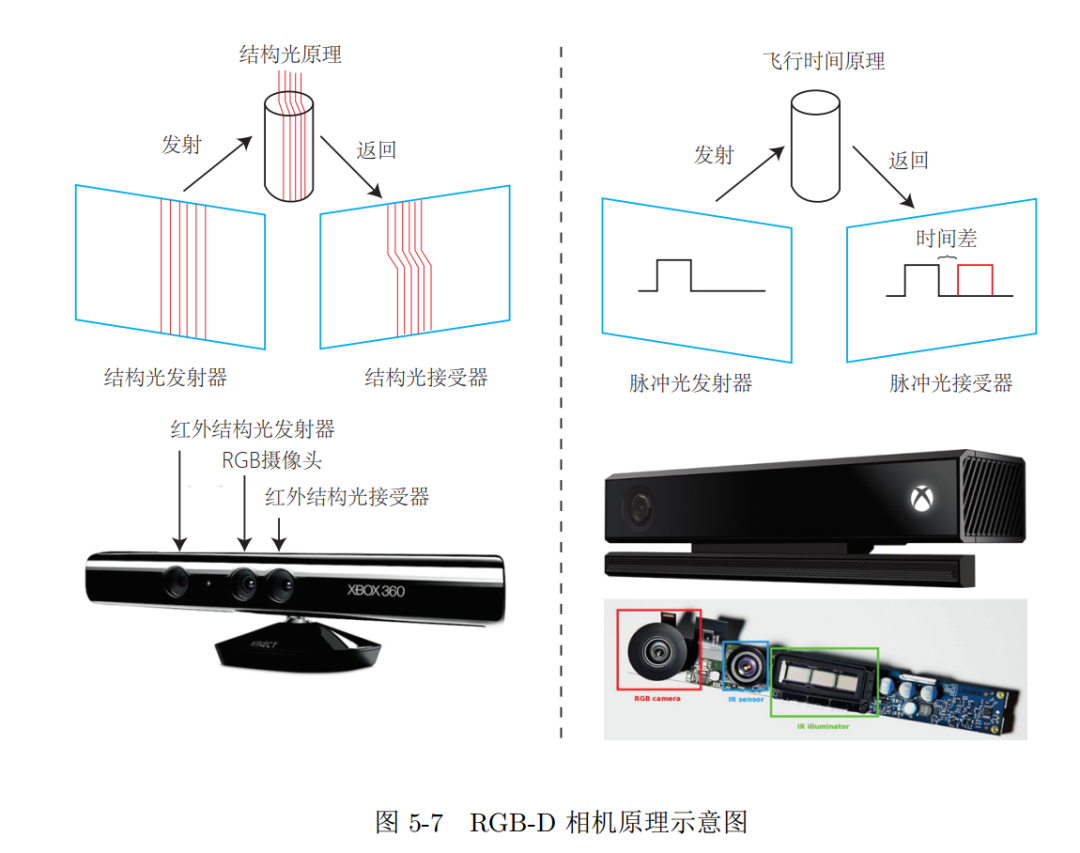
RGB-D相机模型
1 | 不同方法对比 |
| 方法 | 原理 | 例子 |
|---|---|---|
| 红外结构光(Structured Light) | 返回的结构光图案 | Kinect 1,Project Tango 1,Intel RealSense |
| 飞行时间法(Time-of-flight,ToF) | 脉冲光往返时间 | Kinect 2…… |
1 | ToF与激光扫描对比 |
| 方法 | 原理 | 处理 |
|---|---|---|
| ToF | 可获得整个图像像素深度 | 图像、点云 |
| 激光 | 逐点扫描 | 点云不同方法对比 |
图像
1 | 描述 |
数学:矩阵
计算机:连续的磁盘或内存空间(二维数组)
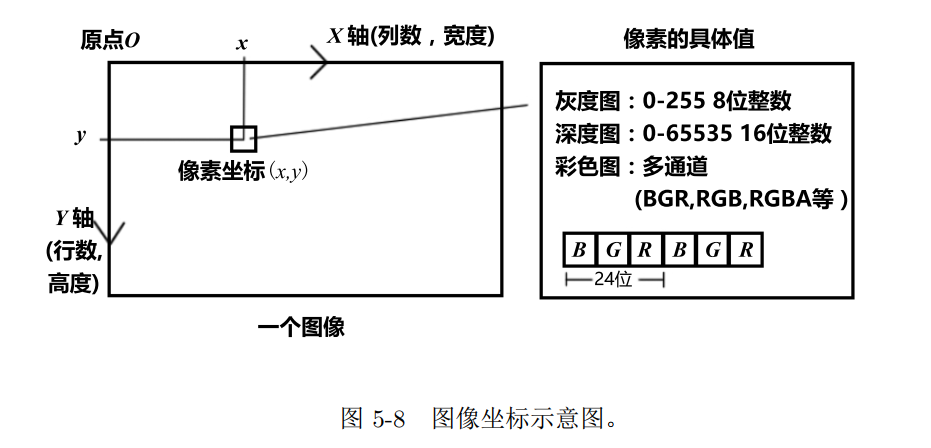
计算机中图像的表示
$$
\boldsymbol{I}(x, y) \in \mathbb{R}^{w \times h}
$$
$(x, y)$ 像素位置, $I(x, y)$ 对应位置上的灰度值, $w, h$ 宽度和高度
1 | unsigned char image[480][640] *//width=640,height=480* |
1 | unsigned char pixel = image[y][x] |