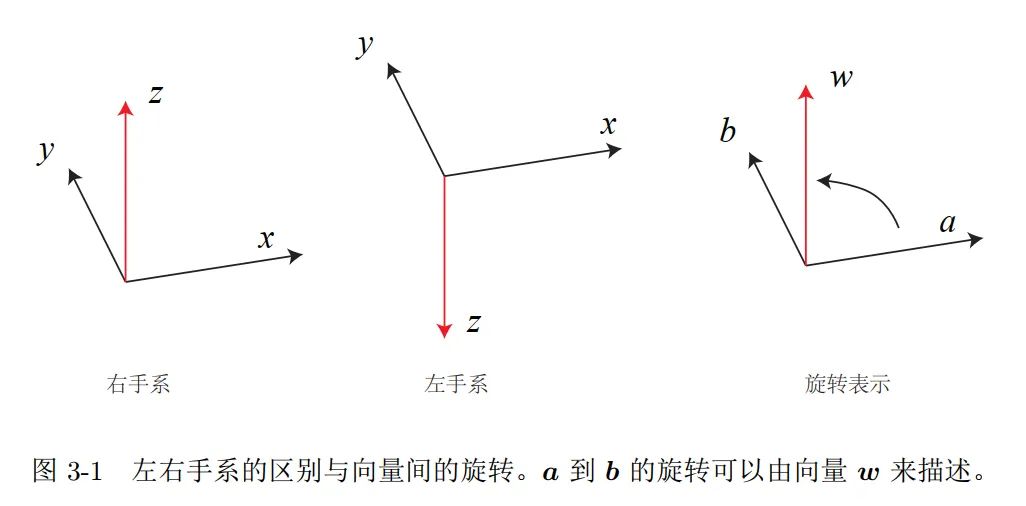
旋转矩阵
点和向量、坐标系
- 坐标系间欧式变换
- 变换矩阵与齐次坐标
旋转向量和欧拉角
旋转向量
- 欧拉角
四元数
定义
- 运算
- 表示旋转
- 四元数和旋转矩阵
相似、 仿射、射影变换
目标:
三维空间刚体运动描述方式
旋转矩阵
- 变换矩阵
- 四元数
- 欧拉角
Eigen库、几何模块
旋转矩阵
点和向量、坐标系
内积
$$
\boldsymbol{a} \cdot \boldsymbol{b}=\boldsymbol{a}^{T} \boldsymbol{b}=\sum_{i=1}^{3} a_{i} b_{i}=|\boldsymbol{a}||\boldsymbol{b}| \cos \langle\boldsymbol{a}, \boldsymbol{b}\rangle
$$
外积
$$
\boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \
a_{1} & a_{2} & a_{3} \
b_{1} & b_{2} & b_{3}
\end{array}\right]=\left[\begin{array}{c}
a_{2} b_{3}-a_{3} b_{2} \
a_{3} b_{1}-a_{1} b_{3} \
a_{1} b_{2}-a_{2} b_{1}
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a_{3} & a_{2} \
a_{3} & 0 & -a_{1} \
-a_{2} & a_{1} & 0
\end{array}\right] \boldsymbol{b} \triangleq \boldsymbol{a}^{\wedge} \boldsymbol{b}
$$
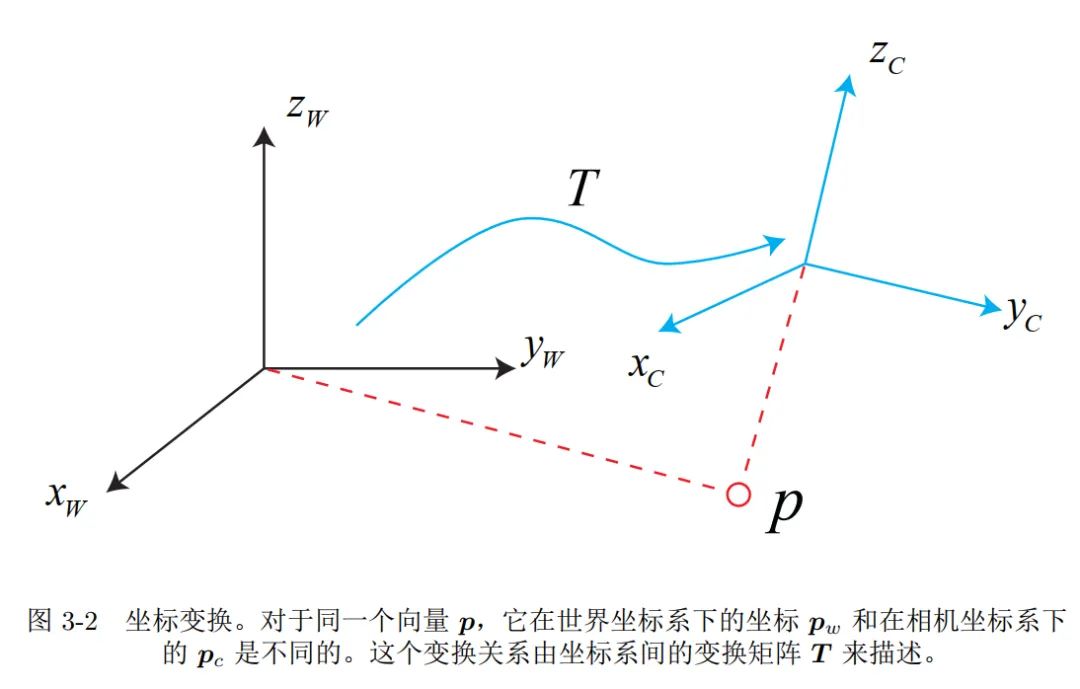
坐标系间欧式变换
世界坐标系、移动坐标系
$$
\begin{aligned}
{\left[\begin{array}{l}
a_{1} \
a_{2} \
a_{3}
\end{array}\right]=} & {\left[\begin{array}{lll}
\boldsymbol{e}{1}^{T} \boldsymbol{e}{1}^{\prime} & \boldsymbol{e}{1}^{T} \boldsymbol{e}{2}^{\prime} & \boldsymbol{e}{1}^{T} \boldsymbol{e}{3}^{\prime} \
\boldsymbol{e}{2}^{T} \boldsymbol{e}{1}^{\prime} & \boldsymbol{e}{2}^{T} \boldsymbol{e}{2}^{\prime} & \boldsymbol{e}{2}^{T} \boldsymbol{e}{3}^{\prime} \
\boldsymbol{e}{3}^{T} \boldsymbol{e}{1}^{\prime} & \boldsymbol{e}{3}^{T} \boldsymbol{e}{2}^{\prime} & \boldsymbol{e}{3}^{T} \boldsymbol{e}{3}^{\prime}
\end{array}\right]\left[\begin{array}{l}
a_{1}^{\prime} \
a_{2}^{\prime} \
a_{3}^{\prime}
\end{array}\right] \triangleq \boldsymbol{R} \boldsymbol{a}^{\prime} } \
S O(n)=&\left{\boldsymbol{R} \in \mathbb{R}^{n \times n} \mid \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right} \
\boldsymbol{a}^{\prime}=\boldsymbol{R}^{-1} \boldsymbol{a}=\boldsymbol{R}^{T} \boldsymbol{a}
\end{aligned}
$$
bold $R$ : 旋转矩阵
$S O(n)$ : 特殊正交群, 旋转矩阵的集合
旋转矩阵性质:旋转矩阵的逆(转置)描述了一个相反的旋转
$$
\boldsymbol{a}^{\prime}=\boldsymbol{R}^{-1} \boldsymbol{a}=\boldsymbol{R}^{T} \boldsymbol{a}
$$
非齐次坐标缺点
$$
\boldsymbol{b}=\boldsymbol{R}{1} \boldsymbol{a}+\boldsymbol{t}{1}, \quad \boldsymbol{c}=\boldsymbol{R}{2} \boldsymbol{b}+\boldsymbol{t}{2} \boldsymbol{c}=\boldsymbol{R}{2}\left(\boldsymbol{R}{1} \boldsymbol{a}+\boldsymbol{t}{1}\right)+\boldsymbol{t}{2}
$$
如此形式变换多次后过于复杂
齐次坐标和变换矩阵
$$
\begin{gathered}
{\left[\begin{array}{l}
a^{\prime} \
1
\end{array}\right]=\left[\begin{array}{ll}
R & t \
0^{T} & 1
\end{array}\right]\left[\begin{array}{l}
a \
1
\end{array}\right] \triangleq T\left[\begin{array}{l}
a \
1
\end{array}\right]} \
S E(3)=\left{\boldsymbol{T}=\left[\begin{array}{cc}
\boldsymbol{R} & \boldsymbol{t} \
\mathbf{0}^{T} & 1
\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in S O(3), \boldsymbol{t} \in \mathbb{R}^{3}\right}
\end{gathered}
$$
通过增加自由度来允许把变换写成线性形式
带来的方便:
$$
\tilde{\boldsymbol{b}}=\boldsymbol{T}{1} \tilde{\boldsymbol{a}}, \tilde{\boldsymbol{c}}=\boldsymbol{T}{2} \tilde{\boldsymbol{b}} \Rightarrow \tilde{\boldsymbol{c}}=\boldsymbol{T}{2} \boldsymbol{T}{1} \tilde{\boldsymbol{a}}
$$
$S E(3)$ :特殊欧式群(Special Euclidean Group)
变换矩阵的逆:
$$
\boldsymbol{T}^{-1}=\left[\begin{array}{cc}
\boldsymbol{R}^{T} & -\boldsymbol{R}^{T} \boldsymbol{t} \
\mathbf{0}^{T} & 1
\end{array}\right]
$$
默认规则
- $T a$ 齐次坐标
- $R a$ 非齐次丛标
旋转向量和欧拉角
1 | 矩阵表示缺点 |
- SO(3)旋转矩阵9个量→1次旋转只有3个自由度;变化矩阵16个量→6自由度变换 冗余
- 旋转矩阵带有约束:正交矩阵且行列式为1 →约束使得求解困难
旋转向量
1 | 旋转向量 |
旋转轴+旋转角
旋转向量 $\rightarrow$ 旋转矩阵
$$
\boldsymbol{R}=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{T}+\sin \theta \boldsymbol{n}^{\wedge} .
$$
旋转矩阵 $\rightarrow$ 旋转向量
$$
\theta=\arccos \left(\frac{\operatorname{tr}(\boldsymbol{R})-1}{2}\right)
$$
来源
$$
\begin{aligned}
\operatorname{tr}(\boldsymbol{R}) &=\cos \theta \operatorname{tr}(\boldsymbol{I})+(1-\cos \theta) \operatorname{tr}\left(\boldsymbol{n} \boldsymbol{n}^{T}\right)+\sin \theta \operatorname{tr}\left(\boldsymbol{n}^{\wedge}\right) \
&=3 \cos \theta+(1-\cos \theta) \
&=1+2 \cos \theta
\end{aligned}
$$
性质:
-算术角度:转轴 $n$ 为矩阵 $R$ 特征值1对应的特征向量
- 几何角度:旋转轴经过旋转后不变
$$
\boldsymbol{R} \boldsymbol{n}=\boldsymbol{n}
$$
欧拉角
1 | 引入 |
欧拉角优点
用直观的方式描述旋转:三个分离的转角
1 | 欧拉角 |
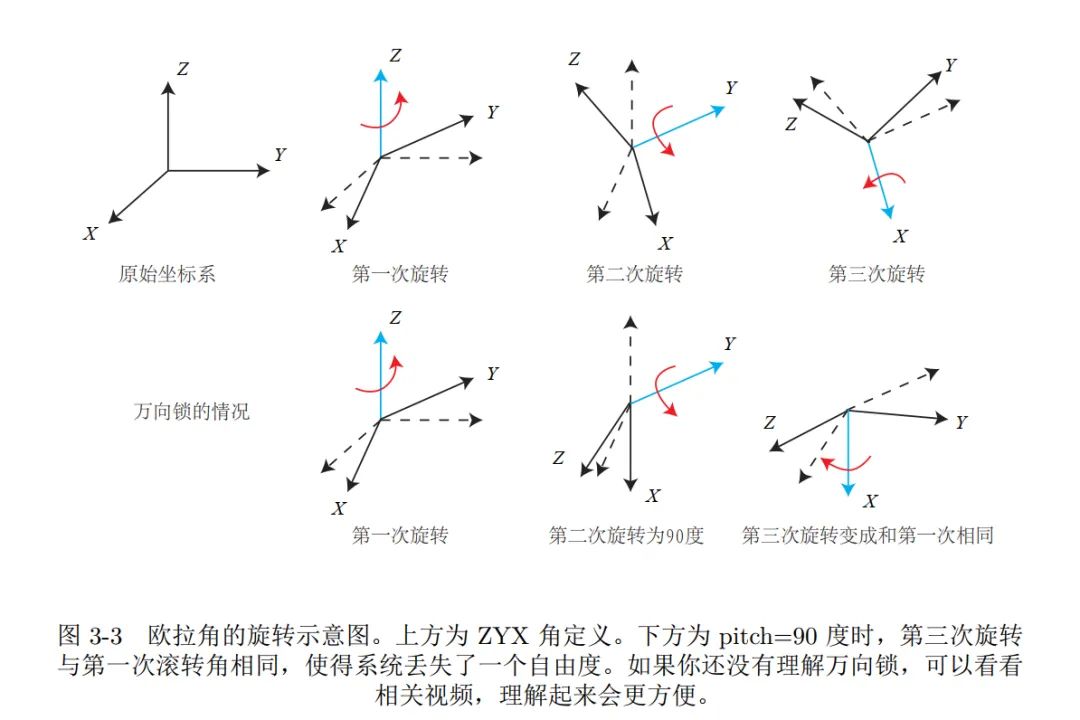
ZYX(rpy)
- 偏航角yaw:绕物体的Z轴旋转
- 俯仰角pitch:绕旋转之后的Y轴旋转
- 滚转角roll:绕旋转之后的X轴旋转
万向锁问题(奇异性问题):
在pitch=90时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度
- 不适应应用场景:插值、迭代、滤波、优化
- 适宜场景:人机交互
四元数
定义
1 | 引入 |
复数平面C上乘上复数相当于逆时针把一个复向量旋转90
特点:紧凑、无歧义性、不够直观、运算稍复杂
定义
$$
\boldsymbol{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k
$$
$\mathrm{ijk}$ 为四元数的三个虚部, 这三个虚部满足关系式:
$$
\left{\begin{array}{l}
i^{2}=j^{2}=k^{2}=-1 \
i j=k, j i=-k \
j k=i, k j=-i \
k i=j, i k=-j
\end{array}\right.
$$
有时人们也用一个标量和一个向量来表达:
$$
\boldsymbol{q}=[s, \boldsymbol{v}], \quad s=q_{0} \in \mathbb{R}, \boldsymbol{v}=\left[q_{1}, q_{2}, q_{3}\right]^{T} \in \mathbb{R}^{3},
$$
其中 $s$ 称为四元数的实部,而 $v$ 称为它的虚部
表示旋转的说明
在四元数中, 任意的旋转都可以由两个互为相反数的四元数表示
旋转 $\rightarrow$ 四元数(绕单位向量 $\boldsymbol{n}=\left[n_{x}, n_{y}, n_{z}\right]^{T}$ 的角度为 $\theta$ 的旋转)
$$
\boldsymbol{q}=\left[\cos \frac{\theta}{2}, n_{x} \sin \frac{\theta}{2}, n_{y} \sin \frac{\theta}{2}, n_{z} \sin \frac{\theta}{2}\right]^{T}
$$
四元数 $\rightarrow$ 旋转轴、旋转角
$$
\left{\begin{array}{l}
\theta=2 \arccos q_{0} \
{\left[n_{x}, n_{y}, n_{z}\right]^{T}=\left[q_{1}, q_{2}, q_{3}\right]^{T} / \sin \frac{\theta}{2}}
\end{array}\right.
$$
运算
加法
$$
\boldsymbol{q}{a} \pm \boldsymbol{q}{b}=\left[s_{a} \pm s_{b}, \boldsymbol{v}{a} \pm \boldsymbol{v}{b}\right]
$$
乘法
$$
\begin{aligned}
\boldsymbol{q}{a} \boldsymbol{q}{b}=& s_{a} s_{b}-x_{a} x_{b}-y_{a} y_{b}-z_{a} z_{b} \
&+\left(s_{a} x_{b}+x_{a} s_{b}+y_{a} z_{b}-z_{a} y_{b}\right) i \
&+\left(s_{a} y_{b}-x_{a} z_{b}+y_{a} s_{b}+z_{a} x_{b}\right) j \
&+\left(s_{a} z_{b}+x_{a} y_{b}-y_{b} x_{a}+z_{a} s_{b}\right) k \
\boldsymbol{q}{a} \boldsymbol{q}{b}=[&\left.s_{a} s_{b}-\boldsymbol{v}{a}^{T} \boldsymbol{v}{b}, s_{a} \boldsymbol{v}{b}+s{b} \boldsymbol{v}{a}+\boldsymbol{v}{a} \times \boldsymbol{v}{b}\right]
\end{aligned}
$$
共轭
$$
\boldsymbol{q}{a}^{}=s_{a}-x_{a} i-y_{a} j-z_{a} k=\left[s_{a},-\boldsymbol{v}_{a}\right] \boldsymbol{q}^{} \boldsymbol{q}=\boldsymbol{q} \boldsymbol{q}^{}=\left[s_{a}^{2}+\boldsymbol{v}^{T} \boldsymbol{v}, \mathbf{0}\right]
$$
模长
$$
\left|\boldsymbol{q}{a}\right|=\sqrt{s{a}^{2}+x_{a}^{2}+y_{a}^{2}+z_{a}^{2}}\left|\boldsymbol{q}{a} \boldsymbol{q}{b}\right|=\left|\boldsymbol{q}{a}\right|\left|\boldsymbol{q}{b}\right|
$$
逆
$$
\boldsymbol{q}^{-1}=\boldsymbol{q}^{} /|\boldsymbol{q}|^{2} q q^{-1}=q^{-1} q=1\left(\boldsymbol{q}{a} \boldsymbol{q}{b}\right)^{-1}=\boldsymbol{q}{b}^{-1} \boldsymbol{q}{a}^{-1}
$$
数乘与点乘
$$
k \boldsymbol{q}=[k s, k \boldsymbol{v}] \boldsymbol{q}{a} \cdot \boldsymbol{q}{b}=s_{a} s_{b}+x_{a} x_{b} i+y_{a} y_{b} j+z_{a} z_{b} k
$$
表示旋转
三维空间点用虚四元数描述
$$
\boldsymbol{p}=[0, x, y, z]=[0, \boldsymbol{v}]
$$
用四元数表示旋转
$$
\boldsymbol{q}=\left[\cos \frac{\theta}{2}, \boldsymbol{n} \sin \frac{\theta}{2}\right]
$$
旋转后的点
$$
p^{\prime}=q p q^{-1}
$$
四元数 4 旋转矩阵
四元数 $\rightarrow$ 旋转矩阵
$$
\boldsymbol{R}=\left[\begin{array}{lll}
1-2 q_{2}^{2}-2 q_{3}^{2} & 2 q_{1} q_{2}+2 q_{0} q_{3} & 2 q_{1} q_{3}-2 q_{0} q_{2} \
2 q_{1} q_{2}-2 q_{0} q_{3} & 1-2 q_{1}^{2}-2 q_{3}^{2} & 2 q_{2} q_{3}+2 q_{0} q_{1} \
2 q_{1} q_{3}+2 q_{0} q_{2} & 2 q_{2} q_{3}-2 q_{0} q_{1} & 1-2 q_{1}^{2}-2 q_{2}^{2}
\end{array}\right]
$$
旋转矩阵 $\rightarrow$ 四元数
$$
q_{0}=\frac{\sqrt{\operatorname{tr}(R)+1}}{2}, q_{1}=\frac{m_{23}-m_{32}}{4 q_{0}}, q_{2}=\frac{m_{31}-m_{13}}{4 q_{0}}, q_{3}=\frac{m_{12}-m_{21}}{4 q_{0}}
$$
相似、仿射、射影变换
欧式变换
保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化
相似变换
$$
\boldsymbol{T}{S}=\left[\begin{array}{ll}
s \boldsymbol{R} & \boldsymbol{t} \
\mathbf{0}^{T} & 1
\end{array}\right]
$$
允许物体进行均匀的缩放
仿射变换
$$
\boldsymbol{T}{\boldsymbol{A}}=\left[\begin{array}{ll}
\boldsymbol{A} & \boldsymbol{t} \
\boldsymbol{0}^{T} & 1
\end{array}\right]
$$
仿射变换不必要求 $A$ 为正交矩阵,只需可逆即可
射影变换
$$
\boldsymbol{T}_{P}=\left[\begin{array}{ll}
\boldsymbol{A} & \boldsymbol{t} \
\mathbf{a}^{T} & v
\end{array}\right]
$$
变换中形式最一般的
$\boldsymbol{A}$ 为可逆矩阵, $\mathrm{a}^{T}$ 为缩放, $\boldsymbol{t}$ 为平移