目标:
- SLAM模块及其任务
- 搭建编程环境
- Linux下编译程序
- cmake使用
引子
1 | 小萝卜 |
自主运动能力轮子、电机
任务
定位$\rightarrow$在什么地方
- 建图$\rightarrow$周围环境如何
传感器
本体$\rightarrow$轮式编码器、相机、激光
- 环境$\rightarrow$导轨、二维码标志
1 | 相机 |
单目相机:只使用一个摄像头进行SLAM(Monocular SLAM)
三维空间的二维投影,故欲恢复三维结构,必须移动相机视角以形成视差从而计算深度。
双目相机(Stereo)
通过某种手段测量物体离我们的距离,克服单目无法知道距离的缺点
由两个单目相机组成,但两个相机之间的距离(Baseline)已知
缺点:计算量大,需要GPU和FPGA加速
深度相机(RGB-D)
通过红外结构光或ToF原理,通过主动向物体发射光并接受返回的光,测出物体离相机的距离
优点:不通过软件计算,而是通过物理的测量手段,节省大量计算量
缺点:测量范围窄、噪声大、视野小、易受日光干扰、无法测量透射材质
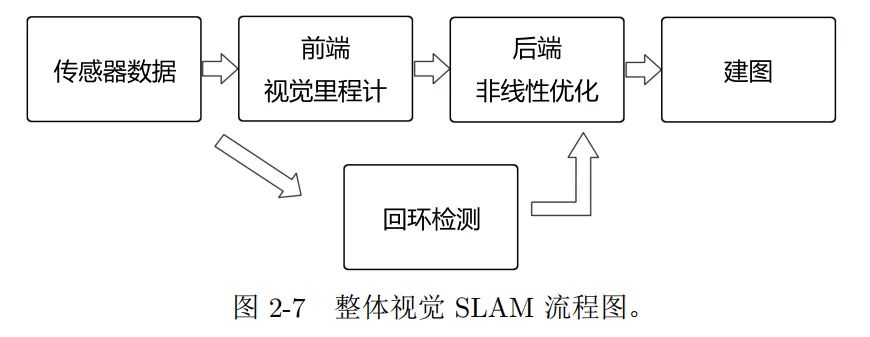
经典视觉SLAM框架
传感器信息读取
- 相机图像信息读取和预处理
- 码盘、惯性传感器信息读取和同步
视觉里程计(Visual Odometry,VO)
- 估算相邻图像间相机的运动,以及局部地图的样子
后端优化(Optimization)
- 接受不同时刻VO测量的相机位姿及回环检测信息,优化后得到全局一致的轨迹和地图
回环检测(Loop Closing)
- 判断机器人是否曾经到达过先前位置
建图(Mapping)
- 根据估计的轨迹,建立与任务要求对应的地图
视觉里程计
1 | 计算机如何通过图像确定相机运动? |
VO能够通过相邻帧间图像估计相机运动,并恢复场景空间结构,只计算相邻时刻运动,和再往前过去的信息没有关联。
缺点:累计漂移
后端优化
1 | 处理SLAM过程中噪声的问题 |
如何从带有噪声的数据中,估计整个系统的状态,以及这个状态估计的不确定性有多大最大后验概率估计(Maximum-a-Posteriori,MAP)
在视觉 SLAM 中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法
1 | SLAM问题的本质 |
对运动主体自身和周围环境空间不确定性的估计
回环检测
1 | 解决位置估计随时间漂移的问题 |
要求机器人具有识别曾经到达过场景的能力
判断图像间的相似性
建图
1 | 构建地图的过程 |
一个相机有6个自由度的运动
- xyz移动自由度
- xyz转动自由度
1 | 度量地图Metric Map |
强调精确表示地图中物体的位置关系
- 稀疏地图:由路标组成的地图→定位
- 稠密地图:按照某种分辨率,由许多个小块组成→导航
1 | 拓扑地图Topological Map |
强调地图元素之间的关系
Graph
节点和边视觉里程计
VO能够通过相邻帧间图像估计相机运动,并恢复场景空间结构,只计算相邻时刻运动,和再往前过去的信息没有关联。
缺点:累计漂移
后端优化
如何从带有噪声的数据中,估计整个系统的状态,以及这个状态估计的不确定性有多大最大后验概率估计(Maximum-a-Posteriori,MAP)
在视觉 SLAM 中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法
对运动主体自身和周围环境空间不确定性的估计
回环检测
要求机器人具有识别曾经到达过场景的能力
判断图像间的相似性
建图
一个相机有6个自由度的运动
- xyz移动自由度
- xyz转动自由度
强调精确表示地图中物体的位置关系
- 稀疏地图:由路标组成的地图→定位
- 稠密地图:按照某种分辨率,由许多个小块组成→导航
强调地图元素之间的关系
Graph
节点和边
SLAM问题的数学表述
什么是运动
从 $k-1$ 时刻到 $k$ 时刻, 位置 $x$ 如何变化
什么是观测
在 $k$ 时刻, 于 $x_{k}$ 处探测到了某一个路标 $y_{j}$, 如何描述
运动方程和观测方程
$$
\boldsymbol{x}{k}=f\left(\boldsymbol{x}{k-1}, \boldsymbol{u}{k}, \boldsymbol{w}{k}\right) \boldsymbol{z}{k, j}=h\left(\boldsymbol{y}{j}, \boldsymbol{x}{k}, \boldsymbol{v}{k, j}\right)
$$
$x_{k}$ : $\mathrm{k}$ 时刻的位置, $x_{k-1}$ : $\mathrm{k}-1$ 时刻的位置, $u_{k}$ : 运动传感器的读数, $w_{k}$ : 噪声
$z_{k, j}$ : 在 $x_{k}$ 位置上看到某个路标点 $y_{j}$ 所产生的观测数据, $v_{k, j}$ 为观测噪声
举例:
参数化方式下的运动方程:
$$
\left[\begin{array}{l}
x \
y \
\theta
\end{array}\right]{k}=\left[\begin{array}{l}
x \
y \
\theta
\end{array}\right]{k-1}+\left[\begin{array}{c}
\Delta x \
\Delta y \
\Delta \theta
\end{array}\right]{k}+\boldsymbol{w}{k}
$$
$\boldsymbol{x}{k}=[x, y, \theta]{k}^{T}$ 位姿, 两个位置 $+$ 个个转角
观测方程:
$$
\left[\begin{array}{c}
r \
\phi
\end{array}\right]=\left[\begin{array}{c}
\sqrt{\left(p_{x}-x\right)^{2}+\left(p_{y}-y\right)^{2}} \
\arctan \left(\frac{p_{y}-y}{p_{x}-x}\right)
\end{array}\right]+\boldsymbol{v}
$$
$\boldsymbol{y}=\left[p_{x}, p_{y}\right]^{T}$ 路标点, $\boldsymbol{z}=[r, \phi]^{T}$ 观测数据
状态估计问题
定义:如何通过带有噪声的测量数据,估计内部的、隐藏着的状态变量
分类
方程是否线性
- 线性系统
- 非线性系统
噪声是否服从高斯分布
- 高斯系统
- 非高斯系统
求解
| Linear | Non-Linear | |
|---|---|---|
| Gaussian | Kalman Filter(KF) | |
| Non-Gaussian | Extended Kalman Filter(EKF) 非线性优化 |
其他方法
粒子滤波器、非线性优化方法、图优化