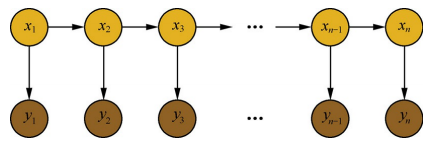
条件随机场(conditional random fields,简称 $CRF$,或$CRFs$),是一种判别式概率模型,常用于标注或分析序列资料,如自然语言文字或是生物序列。
条件随机场是条件概率分布模型P(Y|X),表示的是给定一组输入随机变量X的条件下另一组输出随机变量Y的马尔可夫随机场,也就是说$CRF$的特点是假设输出随机变量构成马尔可夫随机场。
知识框架 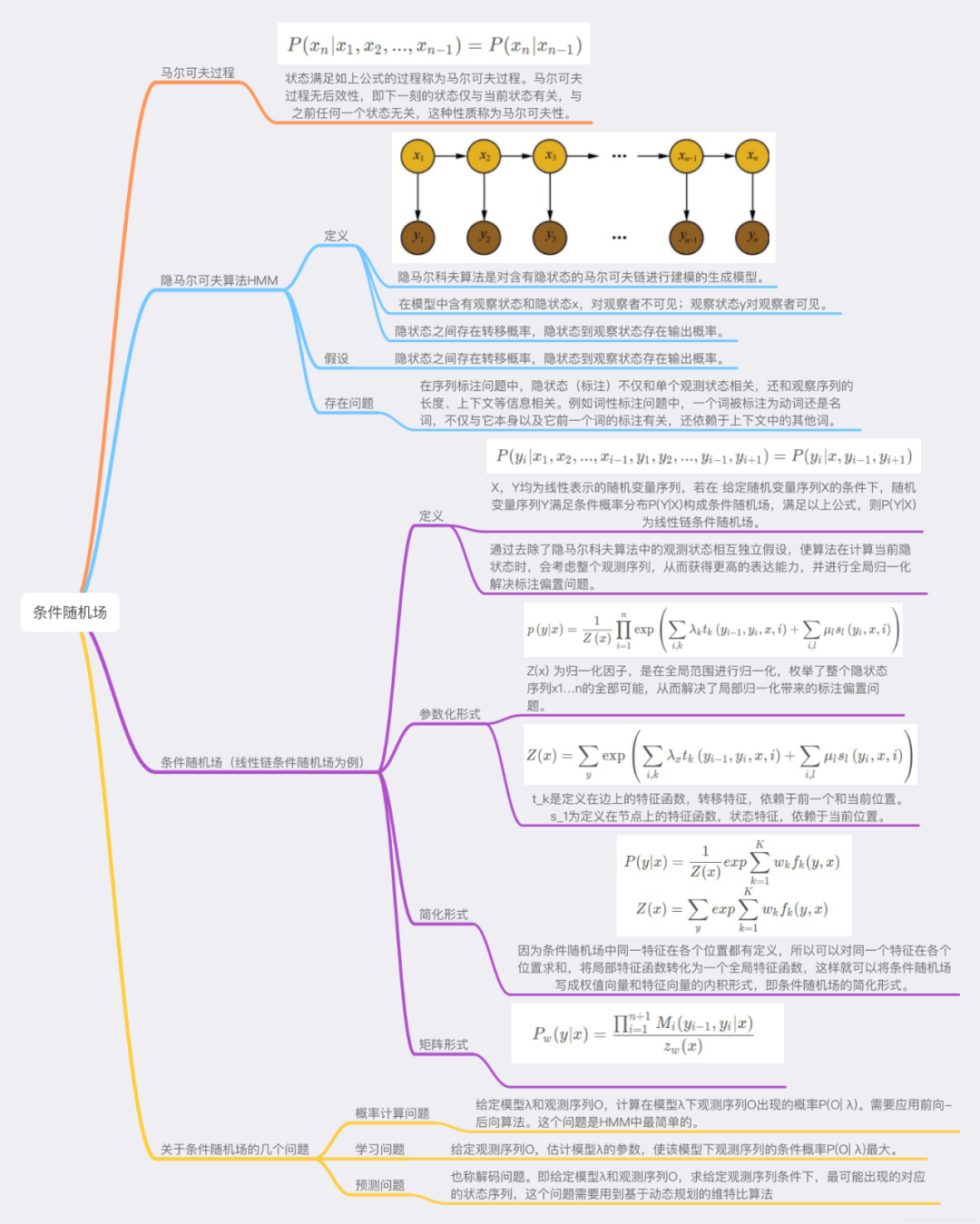
马尔可夫过程
定义:假设一个随机过程中, $t_n$时刻的状态$x_n$的条件发布,只与其前一状态$x_{n-1}$相关,即:
$$
P\left(x_{n} | x_{1}, x_{2}, \ldots, x_{n-1}\right)=P\left(x_{n} | x_{n-1}\right)
$$
则将其称为马尔可夫过程。
隐马尔可夫算法(HMM)
1、定义
隐马尔可夫算法是对含有未知参数(隐状态)的马尔可夫链进行建模的生成模型,如下图所示:
在隐马尔科夫模型中,包含隐状态和观察状态,隐状态$x_i$对于观察者而言是不可见的,而观察状态$y_i$对于观察者而言是可见的。隐状态间存在转移概率,隐状态$x_i$到对应的观察状态$y_i$间存在输出概率。
2、假设
假设隐状态$x_i$的状态满足马尔可夫过程,$i$时刻的状态$x_i$的条件分布,仅与其前一个状态$x_{i-1}$相关,即:
$$
P\left(x_{i} | x_{1}, x_{2}, \ldots, x_{i-1}\right)=P\left(x_{i} | x_{i-1}\right)
$$
假设观测序列中各个状态仅取决于它所对应的隐状态,即:
$$
P\left(y_{i} | x_{1}, x_{2}, \ldots, x_{i-1}, y_{1}, y_{2}, \ldots, y_{i-1}, y_{i+1}, \ldots\right)=P\left(y_{i} | x_{i}\right)
$$
3、存在问题
在序列标注问题中,隐状态(标注)不仅和单个观测状态相关,还和观察序列的长度、上下文等信息相关。例如词性标注问题中,一个词被标注为动词还是名词,不仅与它本身以及它前一个词的标注有关,还依赖于上下文中的其他词
条件随机场
以线性链条件随机场为例
1、定义
给定$X=(x_1,x_2····,x_n)$,$Y=(y_1,y_2····,y_n)$均为线性链表示的随机变量序列,若在给随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔可夫性:
$$
P\left(y_{i} | x_{1}, x_{2}, \ldots, x_{i-1}, y_{1}, y_{2}, \ldots, y_{i-1}, y_{i+1}\right)=P\left(y_{i} | x, y_{i-1}, y_{i+1}\right)
$$
则称$P(Y|X)$为线性链条件随机场。
通过去除了隐马尔科夫算法中的观测状态相互独立假设,使算法在计算当前隐状态$x_i$时,会考虑整个观测序列,从而获得更高的表达能力,并进行全局归一化解决标注偏置问题。
1)参数化形式
$$
p(y | x)=\frac{1}{Z(x)} \prod_{i=1}^{n} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)
$$
其中:$Z(x)$为归一化因子,是在全局范围进行归一化,枚举了整个隐状态序列$x_{1…n}$的全部可能,从而解决了局部归一化带来的标注偏置问题。
$t_k$为定义在边上的特征函数,转移特征,依赖于前一个和当前位置$s_1$为定义在节点上的特征函数,状态特征,依赖于当前位置
2)简化形式
因为条件随机场中同一特征在各个位置都有定义,所以可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场写成权值向量和特征向量的内积形式,即条件随机场的简化形式。
- step 1 将转移特征和状态特征及其权值用统一的符号表示,设有$k_1$个转移特征,$k_2$个状态特征,,记
$$
f_{k}\left(y_{i-1}, y_{i}, x, i\right)=\left{\begin{array}{l}
t_{k}\left(y_{i-1}, y_{i}, x, i\right), \quad k=1,2,3, \ldots, K_{1} \
s_{l}\left(y_{i}, x, i\right), \quad k=k_{1}+l ; l=1,2, \ldots, K_{2}
\end{array}\right.
$$
- step 2 对转移与状态特征在各个位置求$i$和,记作
$$
f_{k}(y, x)=\sum_{i=1}^{n} f_{k}\left(y_{i-1}, y_{i}, x, i\right), k=1,2, \ldots, K
$$
- step 3 将 和 用统一的权重表示,记作
$$
w_{k}=\left{\begin{array}{ll}
\lambda_{k}, & k=1,2, \ldots, K_{1} \
\mu_{l}, & k=K_{1}+l ; l=1,2, \ldots, K_{2}
\end{array}\right.
$$
step 4 转化后的条件随机场可表示为:
$$
\begin{aligned}
P(y | x) &=\frac{1}{Z(x)} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x) \
Z(x) &=\sum_{y} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x)
\end{aligned}
$$- step 5 若 表示权重向量:$w=(w_1,w_2,…,w_k)^T$以$F(y,x)$表示特征向量,即
$$
F(y, x)=\left(f_{1}(y | x), f_{2}(y | x), \ldots, f_{K}(y | x)\right)^{T}
$$
则,条件随机场写成内积形式为:
$$
\begin{array}{l}
P_{w}(y | x)=\frac{\exp (w \cdot F(y, x)}{Z_{w}(x)} \
Z_{w}(x)=\sum_{y} \exp (w \cdot F(y, x))
\end{array}
$$
- step 5 若 表示权重向量:$w=(w_1,w_2,…,w_k)^T$以$F(y,x)$表示特征向量,即
3)矩阵形式
$$
P_{w}(y | x)=\frac{1}{Z_{w}(x)} \prod_{i=1}^{n+1} M_{i}\left(y_{i-1}, y_{i} | x\right)
$$
2、基本问题
条件随机场包含概率计算问题、学习问题和预测问题三个问题。
- 概率计算问题:已知模型的所有参数,计算观测序列Y出现的概率,常用方法:前向和后向算法;
- 学习问题:已知观测序列Y,求解使得该观测序列概率最大的模型参数,包括隐状态序列、隐状态间的转移概率分布和从隐状态到观测状态的概率分布,常用方法:Baum-Wehch算法;
- 预测问题:一直模型所有参数和观测序列Y,计算最可能的隐状态序列X,常用算法:维特比算法。
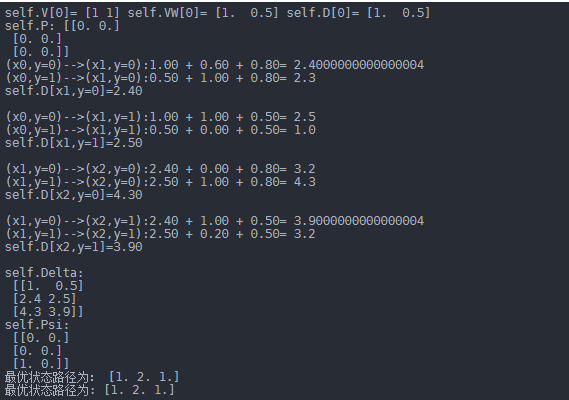
案例:利用维特比算法计算给定输入序列$x$对应的最优输出序列$y^*$:
$$
\max \sum_{i=1}^{3} w \cdot F_{i}\left(y_{i-1}, y_{i}, x\right)
$$
1.初始化
$$
\delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\operatorname{start}, y_{1}=j, x\right), j=1,2 i=1, \delta_{1}(1)=1, \delta_{1}(2)=0.5
$$
2.递推,对$i=2,3,…,n$
$$
\begin{array}{c}
i=2, \delta_{2}(l)=\max {j}\left{\delta{1}(j)+w \cdot F_{2}(j, l, x)\right} \
\delta_{2}(1)=\max \left{1+\lambda_{2} t_{2}, 0.5+\lambda_{4} t_{4}\right}=1.6, \Psi_{2}(1)=1 \
\delta_{2}(2)=\max \left{1+\lambda_{1} t_{1}+\mu_{2} s_{2}, 0.5+\mu_{2} s_{2}\right}=2.5, \Psi_{2}(2)=1 \
i=3, \delta_{3}(l)=\max {j}\left{\delta{2}(j)+w \cdot F_{3}(j, l, x)\right} \
\delta_{3}(1)=\max \left{1.6+\mu_{5} s_{5}, 2.5+\lambda_{3} t_{3}+\mu_{3} s_{3}\right}=4.3, \Psi_{3}(1)=2 \
\delta_{3}(2)=\max \left{1.6+\lambda_{1} t_{1}+\mu_{4} s_{4}, 2.5+\lambda_{5} t_{5}+\mu_{4} s_{4}\right}=4.3, \Psi_{3}(2)=1
\end{array}
$$
3.终止
$$
\max {y}(w \cdot F(y, x))=\max \delta{3}(l)=\delta_{3}(1)=4.3 y_{3}^{}=\operatorname{argmax}{1} \delta{3}(l)=1
$$
4.返回路径
$$
\begin{aligned}
y_{2}^{}=& \Psi_{3}\left(y_{3}^{}=\Psi_{3}(1)=2 y_{1}^{}=\Psi_{2}\left(y_{2}^{}\right)=\Psi_{2}(2)=1\right.\
求得最优路径y^{}=\left(y_{1}^{}, y_{2}^{}, \ldots, y_{n}^{*}\right)=(1,2,1)
\end{aligned}
$$
代码实现如下:
1 |
|
输出结果如下: